Мультиобъективные алгоритмы оптимизации

Мультиобъективное определение оптимизации

Существует два Optimization Toolbox™ мультиобъективных решателя: fgoalattain и fminimax.

fgoalattain решает задачу сокращения множества нелинейных функций _Fi (x) ниже набора _F*i целей. Поскольку _Fi функций (x) несколько, не всегда понятно, что значит решить эту задачу, особенно когда невозможно достичь всех целей одновременно. Поэтому задача переформулируется на задачу, которая всегда четко определена.
Цель unscaled goal attainment problem в том, чтобы минимизировать максимум _Fi (x ) - _F*i.
Существует полезное обобщение немасштабированной задачи. Учитывая набор положительных _wi весов, goal attainment problem пытается найти x, чтобы минимизировать максимум
$\frac{F_{i} (x) - F_{i}^{*}}{w_{i}} .$ (1)
Эта минимизация, как предполагается, достигнута, удовлетворяя все типы ограничений: c (<reservedrangesplaceholder9>) ≤ 0 , ceq (<reservedrangesplaceholder7>) = 0, <reservedrangesplaceholder6> ≤ <reservedrangesplaceholder5>, Aeq·x = beq, и <reservedrangesplaceholder2> ≤ <reservedrangesplaceholder1> ≤ <reservedrangesplaceholder0>.
Если вы задаете все веса равными 1 (или любой другой положительной константе), задача достижения цели является такой же, как и неотмеренная задача достижения цели. Если _F*i положительны, и вы устанавливаете все веса как _wi = _F*i, задача достижения цели становится минимизирующее относительное различие между _Fi функций (x) и _F*i целей.
Другими словами, задача достижения цели состоит в том, чтобы минимизировать γ переменной ослабления, заданную как максимальное i выражений в Уравнении 1. Это подразумевает выражение, которое является формальным оператором задачи достижения цели:
$\min_{x, γ} γ$
таким образом, что F (<reservedrangesplaceholder14>) - w · <reservedrangesplaceholder12> ≤ <reservedrangesplaceholder11> , c (<reservedrangesplaceholder9>) ≤ 0, ceq (<reservedrangesplaceholder7>) = 0, <reservedrangesplaceholder6> ≤ <reservedrangesplaceholder5>, Aeq·x = beq, и <reservedrangesplaceholder2> ≤ <reservedrangesplaceholder1> ≤ <reservedrangesplaceholder0>.
fminimax решает задачу минимизации максимума множества нелинейных функций, удовлетворяющих всем типам ограничений:
$\min_{x} \max_{i} F_{i} (x)$
таким образом, что c (<reservedrangesplaceholder9>) ≤ 0 , ceq (<reservedrangesplaceholder7>) = 0, <reservedrangesplaceholder6> ≤ <reservedrangesplaceholder5>, Aeq·x = beq, и <reservedrangesplaceholder2> ≤ <reservedrangesplaceholder1> ≤ <reservedrangesplaceholder0>.
Очевидно, что эта задача является частным случаем неограниченной задачи достижения цели с _F*i = 0 и _wi = 1.

Алгоритмы

Метод достижения цели

В этом разделе описывается метод достижения цели Gembicki [3]. Этот метод использует набор целей проекта, $F^{*} = {F_{1}^{*}, F_{2}^{*}, ..., F_{m}^{*}}$ , сопоставленный с набором целей, F (x) = {_F 1 (x₎, F 2 (x)_,..., Fm (x)}. Формулировка задачи позволяет недооценивать цели или их обзор, что позволяет проектировщику быть относительно неточным в отношении начальных целей проекта. Относительная степень недо- или перехвата целей управляется вектором весовых коэффициентов_, w = {w 1_, w 2,..., wm}, и выражается как стандартная задача оптимизации с помощью формулировки

\underset{γ \in ℜ, x \in Ω}{minimize} γ

(2)

таким, что $F_{i} (x) - w_{i} γ \leq F_{i}^{*}, i = 1, ..., m .$

Термин _wiγ вводит в проблему элемент слабости, который в противном случае накладывает, чтобы цели были жестко достигнуты. Вектор взвешивания, w, позволяет конструктору выразить меру относительных компромиссов между целями. Например, установка вектора взвешивания w равной начальным целям, указывает, что достигается тот же процент недо- или перехвата целей, F*. Можно включить жесткие ограничения в проект, установив конкретный весовой коэффициент равным нулю (т.е. _wi = 0). Метод достижения цели обеспечивает удобную интуитивно понятную интерпретацию задачи проекта, которая решаема с помощью стандартных процедур оптимизации. Иллюстративные примеры использования метода достижения цели в разработке системы управления можно найти во Флеминге ([10] и [11]).

Метод достижения цели представлен геометрически на рисунке ниже в двух размерностях.

Рисунок 7-1, Геометрическое представление метода достижения цели

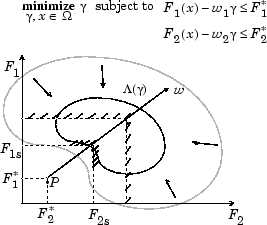
Спецификация целей, ${F_{1}^{*}, F_{2}^{*}}$ , определяет точку цели, P. Вектор надбавки определяет направление поиска от P до выполнимого пространства функции, Λ (<reservedrangesplaceholder5>). Во время оптимизации γ изменяется, что изменяет размер допустимой области. Границы ограничений сходятся к _{уникальной} точке решения F 1 s F 2 s.

Усовершенствования алгоритма для метода достижения цели

Метод достижения цели имеет то преимущество, что он может быть поставлен как нелинейная задача программирования. Характеристики задачи могут также использоваться в нелинейном алгоритме программирования. В последовательном квадратичном программировании (SQP) выбор функции заслуг для поиска линии не прост, потому что во многих случаях трудно «определить» относительную важность между улучшением целевой функции и уменьшением нарушений ограничений. Это привело к ряду различных схем построения функции заслуг (см., например, Schittkowski [36]). В программировании достижения цели может быть более подходящая функция заслуг, которую вы можете достичь, представив Уравнение 2 как задачу минимакса

\underset{x \in ℜ^{n}}{minimize} \max_{i} {Λ_{i}},

(3)

где

$Λ_{i} = \frac{F_{i} (x) - F_{i}^{*}}{w_{i}}, i = 1, ..., m .$

Следуя аргументу Брайтона и др. [1] для минимаксной оптимизации с использованием SQP, использование функции заслуг уравнения 30 для задачи достижения цели уравнения 3 дает

ψ (x, γ) = γ + \sum_{i = 1}^{m} r_{i} \cdot \max {0, F_{i} (x) - w_{i} γ - F_{i}^{*}} .

(4)

Когда функция заслуг 4 Уравнения используется как базис процедуры поиска линии, тогда, хотя ψ (x, γ) может уменьшиться для шага в заданном поисковом направлении, функция max , i может парадоксально увеличиться. Это - принятие деградации в худшем случае. Поскольку цель наихудшего случая отвечает за значение γ целевой функции, это принятие шага, который в конечном счете увеличивает целевую функцию, которая будет минимизирована. И наоборот, ψ (x, γ) может увеличиться, когда max .R. i уменьшается, подразумевая отказ от шага, который улучшает цель наихудшего случая .

Следуя линиям Brayton et al. [1], поэтому решение состоит в том, чтобы задать ψ (x) равным цели наихудшего случая, т.е.,

ψ (x) = \max_{i} Λ_{i} .

(5)

Задачей в способе достижения цели является то, что для включения жестких ограничений обычно используется весовой коэффициент, равный 0. Функция заслуг Уравнения 5 затем становится бесконечной для произвольных нарушений ограничений.

Чтобы преодолеть эту задачу, сохраняя функции Уравнения 5, функция заслуг объединяется с функцией Уравнения 31, давая следующее:

ψ (x) = \sum_{i = 1}^{m} {\begin{array}{l} r_{i} \cdot \max {0, F_{i} (x) - w_{i} γ - F_{i}^{*}} & если w_{i} = 0 \\ \max_{i} Λ_{i}, i = 1, ..., m & иначе . \end{array}

(6)

Другой функцией, которую можно использовать в SQP, является γ целевой функции. Из уравнений KKT можно показать, что приближение к Гессиану Лагрангиана, H, должно иметь нули в строках и столбцах, сопоставленных с переменной γ. Однако это свойство не отображается, если H инициализирована как матрица тождеств. Поэтому H инициализируется и поддерживается так, чтобы иметь нули в строках и столбцах, сопоставленных с γ.

Эти изменения делают Гессиан, H, бессрочным. Поэтому H установлено, что нули в строках и столбцах сопоставлены с γ, за исключением диагонального элемента, который установлен на небольшое положительное число (например 1e-10). Это позволяет использовать быстро сходящийся положительно определенный метод QP, описанный в Quadratic Programming Solution.

Предыдущие изменения были реализованы в fgoalattain и были найдены, чтобы сделать метод более устойчивым. Однако из-за быстрой сходимости метода SQP требование, чтобы функция заслуг строго уменьшалась, иногда требует больших вычислений функции, чем реализация SQP, использующая функцию заслуг уравнения 30.

Минимизация максимальной цели

fminimax использует метод достижения цели. Это принимает цели 0, и веса 1. С помощью этой формулировки задача достижения цели становится

$\min_{i} \max_{x} (\frac{f_{i} (x) - g o a l_{i}}{w e i g h t_{i}}) = \min_{i} \max_{x} f_{i} (x),$

которая является минимаксной задачей.

Круглые скобки, вы можете ожидать fminimax превратить мультиобъективную функцию в одну цель. Функция

f (<reservedrangesplaceholder5>) = макс. (F 1 (<reservedrangesplaceholder3>)... <reservedrangesplaceholder2> <reservedrangesplaceholder1> (<reservedrangesplaceholder0>))

является единственной целевой функцией для минимизации. Однако он не является дифференцируемым, и цели Optimization Toolbox должны быть плавными. Поэтому задача минимакса сформулирована как задача плавного достижения цели.

Ссылки

[1] Brayton, R. K., S. W. Директор, Г. Д. Хэчтель, и Л.Видигэл, «Новый Алгоритм для Статистического Проектирования схем На основе Методов Квазиньютона и Разделения Функции», Сделки IEEE на Схемах и Системах, издании CAS-26, стр 784-794, сентябрь 1979.

[2] Fleming, P.J. and A.P. Pashkevich, Computer Aided Control System Design With a Multi-Objective Optimization Concerence, Control 1985, Cambridge, UK, pp. 174-179.

[3] Gembicki, F.W., «Вектор оптимизация для управления с Эффективностью и Чувствительностью параметров Индексов», Ph.D. Диссертация, Case Western Reserve Univ., Кливленд, OH, 1974.

[4] Grace, A.C.W., «Computer-Aided Control System Design Using Optimization Technologies», Ph.D. Дипломная работа, Университет Уэльса, Бангор, Гвинед, Великобритания, 1989 год.

[5] Han, S.P., «A Globally Convergent Method For Nonlinear Programming», Journal of Optimization Theory and Applications, Vol. 22, p. 297, 1977.

[6] Madsen, K. and H. Schjaer-Jacobsen, «Algorithms for Nest Case Tolerance Optimization», IEEE Trans. of Circuits and Systems, Vol. CAS-26, Sept. 1979.

[7] Пауэлл, M.J.D., «Быстрый Алгоритм для Нелинейных Ограниченных Вычислений Оптимизации», Числовой Анализ, редактор Г.А. Уотсон, Примечания Лекции в Математике, Издании 630, Springer Verlag, 1978.

Документация