Без ограничений минимизация является задачей нахождения вектора x, которая является локальным минимумом к скалярной функции f (x):
Термин без ограничений означает, что никакое ограничение не помещается в область значений x.
fminunc trust-region АлгоритмМногие методы, используемые в решателях Optimization Toolbox™, основаны на доверительных областях, простой, но мощной концепции в оптимизации.
Чтобы понять подход доверительной области к оптимизации, рассмотрим задачу минимизации без ограничений, минимизируйте f (x), где функция принимает векторные аргументы и возвращает скаляры. Предположим, что вы находитесь в точке, x в n -пространство, и вы хотите улучшить, т.е. переместиться в точку с более низким значением функции. Основная идея состоит в том, чтобы аппроксимировать f с более простой функциональной q, которая разумно отражает поведение функциональной f в окрестности N вокруг точечной x. Этот район - доверительная область. Пробный шаг s вычисляется путем минимизации (или приблизительно минимизации) по N. Это подпрограмма доверительной области,
| (1) |
Текущая точка обновляется следующим образом x + s, если f ( x + s ) < f (x); в противном случае текущая точка остается неизменной и N, область доверия, сокращается, и расчет пробного шага повторяется.
Ключевыми вопросами в определении конкретного подхода доверительной области к минимизации f (x) являются то, как выбрать и вычислить q приближения (заданную в текущей точке x), как выбрать и изменить N доверительной области и как точно решить подблем доверительной области. Этот раздел посвящен проблеме без ограничений. Более поздние разделы обсуждают дополнительные осложнения из-за наличия ограничений на переменные.
В стандартном методе доверительной области ([48]) квадратичное q приближения определяется первыми двумя слагаемыми приближения Тейлора к F при x; окрестность N обычно сферическая или эллипсоидальная по форме. Математически подпрограмма доверительной области обычно указывается
| (2) |
где g - градиент f в текущей точке x, H - матрица Мешковины (симметричная матрица вторых производных), D - диагональная матрица масштабирования, Δ - положительная скалярная величина и ∥. ∥ - 2-норма. Хорошие алгоритмы существуют для решения уравнения 2 (см. [48]); такие алгоритмы обычно включают в себя расчет всех собственных значений H и процесс Ньютона, примененный к светскому уравнению
Такие алгоритмы обеспечивают точное решение уравнения 2. Однако они требуют времени, пропорционального нескольким факторизациям H. Поэтому для масштабных проблем нужен другой подход. В литературе было предложено несколько аппроксимационных и эвристических стратегий, основанных на уравнении 2 ([42] и [50]). Подход приближения, используемый в решателях Optimization Toolbox, состоит в том, чтобы ограничить подблиму доверительной области двумерной подпространственной S ([39] и [42]). После вычисления S подпространства работа по решению Уравнения 2 тривиальна, даже если необходима полная собственная/собственная информация (поскольку в подпространстве задача является только двумерной). Доминирующая работа теперь сместилась на определение подпространства.
Двумерный подпространственный S определяется с помощью предварительно обусловленного сопряженного градиентного процесса, описанного ниже. Решатель определяет S как линейное пространство, охватываемое s 1 и s 2, где s 1 находится в направлении градиента g, и s 2 является либо приблизительным направлением Ньютона, т.е. решением
| (3) |
или направление отрицательной кривизны,
| (4) |
Философия этого выбора S состоит в том, чтобы форсировать глобальное сходимость (через направление наискорейшего спуска или направление отрицательной кривизны) и достичь быстрого локального сходимости (через шаг Ньютона, когда он существует).
Эскиз без ограничений минимизации с использованием идей доверительной области теперь легко дать:
Сформулируйте двумерную подпрограмму доверительной области.
Решите уравнение 2, чтобы определить пробный шаг s.
Если f (x + s) <f (<reservedrangesplaceholder3>), то x = x + s.
Отрегулируйте
Эти четыре шага повторяются до сходимости. Размерность Β доверительной области регулируется согласно стандартным правилам. В частности, это уменьшено, если шаг испытания не принят, т.е. f (x + s) ≥ <reservedrangesplaceholder1> (<reservedrangesplaceholder0>). Для обсуждения этого аспекта см. [46] и [49].
Решатели Optimization Toolbox обрабатывают несколько важных особых случаев f со специализированными функциями: нелинейные методы наименьших квадратов, квадратичные функции и линейные методы наименьших квадратов. Однако базовые алгоритмические идеи те же, что и в общем случае. Эти особые случаи рассматриваются в последующих разделах.
Популярным способом решения больших, симметричных, положительно определенных систем линейных уравнений Hp = - g является метод Предварительно обусловленных сопряженных градиентов (PCG). Этот итеративный подход требует способности вычислять матрично-векторные продукты вида H·v где v является произвольным вектором. Симметричная положительная определенная матричная M является предварительным условием для H. То есть M = C2, где C–1HC–1 является хорошо обусловленной матрицей или матрицей с кластеризованными собственными значениями.
В контексте минимизации можно предположить, что H матрицы Гессия симметрична. Однако H гарантированно будет положительно определено только в окрестности сильного минимизатора. Алгоритм PCG выходит, когда он сталкивается с направлением отрицательной (или нулевой) кривизны, то есть dTHd ≤ 0. Выходное направление PCG p является либо направлением отрицательной кривизны, либо приблизительным решением системы Ньютона Hp = - g. В любом случае p помогает задать двумерный подпространство, используемый в подходе доверительной области, обсуждаемом в Методах доверительной области для нелинейной минимизации.
fminunc quasi-newton АлгоритмХотя существует широкий спектр методов для оптимизации без ограничений, методы могут быть широко классифицированы в терминах производной информации, которая используется или не используется. Методы поиска, которые используют только вычисления функции (например, симплексный поиск Nelder и Mead [30]), наиболее подходят для задач, которые не являются гладкими или имеют ряд разрывов. Методы градиента обычно более эффективны, когда функция, которая будет минимизирована, непрерывна в своей первой производной. Методы более высокого порядка, такие как метод Ньютона, только действительно подходят, когда информация второго порядка легко и легко вычисляется, потому что вычисление информации второго порядка, используя числовую дифференциацию, является вычислительно дорогим.
Методы градиента используют информацию о наклоне функции, чтобы диктовать направление поиска, где минимум, как считается, лежит. Самым простым из них является метод наискорейшего спуска, в котором поиск выполняется в направлении, - ∇ f (x), где ∇ f (x) является градиентом целевой функции. Этот метод очень неэффективен, когда функция, которая будет минимизирована, имеет длинные узкие овраги, как, например, случай с функцией Розенбрка
| (5) |
Минимум этой функции находится в x = [1,1], где f (x ) = 0. Контурная карта этой функции показана на рисунке ниже, вместе с путем решения до минимума для реализации наискорейшего спуска, начиная с точки [-1,9,2]. Оптимизация была прекращена после 1000 итераций, все еще на значительном расстоянии от минимума. Черные области находятся там, где метод постоянно зигзагообразно с одной стороны оврага на другую. Обратите внимание, что к центру графика делается ряд больших шагов, когда точка приземляется точно в центре оврага.
Рисунок 5-1, Метод наискорейшего спуска на функцию Розенбрка
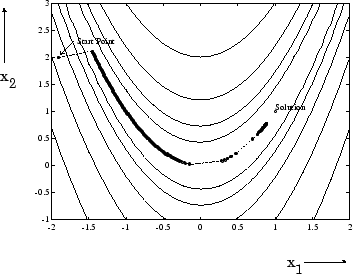
Эта функция, также известная как функция банана, печально известна в неограниченных примерах из-за того, как кривизна изгибается вокруг источника. Функция Розенбрка используется на протяжении всего этого раздела, чтобы проиллюстрировать использование различных методов оптимизации. Контуры были нанесены с экспоненциальными шагами из-за крутизны склона, окружающего U-образный овраг.
Более полное описание этого рисунка, включая скрипты, которые генерируют итерационные точки, смотрите в Banana Function Minimization.
Из методов, которые используют градиентную информацию, наиболее предпочтительными являются методы квази-Ньютона. Эти методы наращивают информацию кривизны при каждой итерации, чтобы сформулировать квадратичную задачу модели вида
| (6) |
где матрица Гессия, H, является положительно определенной симметричной матрицей, c является постоянным вектором, а b является константой. Оптимальное решение для этой задачи происходит, когда частные производные x переходят в нуль, т.е.,
| (7) |
Оптимальная точка решения, x *, может быть записана как
| (8) |
Методы Ньютона (в отличие от методов квази-Ньютона) вычисляют H непосредственно и идут в направлении спуска, чтобы найти минимум после ряда итераций. Вычисление H численно включает в себя большое количество расчетов. Методы квазиньютона избегают этого при помощи наблюдаемого поведения f (<reservedrangesplaceholder3>) и <reservedrangesplaceholder2> (<reservedrangesplaceholder1>), чтобы создать информацию об искривлении, чтобы сделать приближение к H, используя соответствующий метод обновления.
Разработано большое количество гессианских методов обновления. Однако наиболее эффективными для использования в методе общего назначения считаются формулы Broyden [3], Fletcher [12], Goldfarb [20] и Shanno [37] (BFGS).
Формула, заданная BFGS,
| (9) |
где
В качестве отправной точки H 0 может быть задана любая симметричная положительно определенная матрица, например, единичная матрица I. Чтобы избежать инверсии Гессианской H, можно вывести метод обновления, который избегает прямой инверсии H с помощью формулы, которая делает приближение обратной Гессианской H–1 при каждом обновлении. Хорошо известной процедурой является формула DFP Davidon [7], Fletcher и Powell [14]. Это использует ту же формулу, что и метод BFGS (уравнение 9), за исключением того, что qk заменяется на sk.
Информация о градиенте либо передается через аналитически вычисленные градиенты, либо выводится частными производными с помощью численного метода дифференцирования через конечные различия. Это включает возмущение каждой из конструктивных переменных, x, в свою очередь, и вычисление скорости изменения целевой функции.
На каждой основной итерации, k, выполняется поиск линии в направлении
| (10) |
Метод квази-Ньютона проиллюстрирован путем решения функции Розенбрка на фигуре 5-2, метод BFGS на функции Розенбрка. Метод способен следовать форме оврага и сходится к минимуму после 140 вычислений функции, используя только конечные градиенты различий.
Рисунок 5-2, Метод BFGS по функции Розенбрка
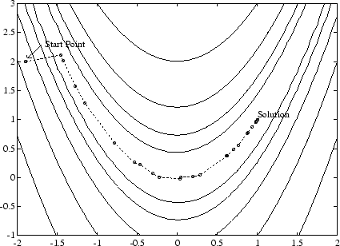
Более полное описание этого рисунка, включая скрипты, которые генерируют итерационные точки, смотрите в Banana Function Minimization.
Линия search является методом поиска, который используется как часть большего алгоритма оптимизации. На каждом шаге основного алгоритма метод поиска по линии ищет вдоль линии, содержащей текущую точку, xk, параллельно направлению поиска, которое является вектором, определяемым основным алгоритмом. То есть метод находит следующую итерацию x k + 1 вида
| (11) |
где xk обозначает текущий итерат, dk является направлением поиска, а α * является скалярным параметром длины шага.
Метод поиска линии пытается уменьшить целевую функцию вдоль линии xk + α * dk путем многократного минимизации полиномиальных моделей интерполяции целевой функции. Процедура поиска по линии состоит из двух основных шагов:
Фаза скобок определяет область значений точек на линии для поиска. Скобка соответствует интервалу, задающему область значений значений α.
Шаг сечения делит скобку на подынтервалы, на которых минимум целевой функции аппроксимируется полиномиальной интерполяцией.
Получившаяся длина шага α удовлетворяет условиям Вульфа:
| (12) |
| (13) |
где c 1 и c 2 являются постоянными с 0 < c 1 < c 2 < 1.
Первое условие (Уравнение 12) требует, чтобы αk достаточно уменьшало целевую функцию. Второе условие (уравнение 13) гарантирует, что длина шага не слишком мала. Точки, которые удовлетворяют обоим условиям (Уравнение 12 и Уравнение 13), называются приемлемыми точками.
Метод поиска линии является реализацией алгоритма, описанного в разделе 2-6 [13]. Для получения дополнительной информации о поиске по линии см. также [31].
Многие из оптимизационных функций определяют направление поиска путем обновления матрицы Гессия при каждой итерации, используя метод BFGS (уравнение 9). Функция fminunc также предоставляет опцию использовать метод DFP, указанный в Quasi-Newton Methods (set HessUpdate на 'dfp' в options для выбора метода DFP). Гессиан, H, всегда поддерживается положительно определенным, так что направление поиска, d, всегда в направлении спуска. Это означает, что для некоторых произволен небольшой шаг α в d направлении, целевая функция уменьшается в величину. Вы достигаете положительной определенности H, гарантируя, что H инициализировано, чтобы быть положительно определенным и после этого (из Уравнения 14) всегда положительно. Термин является продуктом линии параметра длины шага поиска αk и комбинации d направления поиска с прошлыми и настоящими градиентными вычислениями,
| (14) |
Вы всегда достигаете условия, что положительный при выполнении достаточно точного поиска по линии. Это потому, что направление поиска, d, является направлением спуска, так что αk и отрицательный градиент - ∇ f (xk)Td всегда положительны. Таким образом, возможный отрицательный термин - ∇ f (x k + 1)Td может быть сделано настолько маленьким по величине, насколько требуется путем повышения точности поиска линии.