step

Системный объект: фазированный. SumDifferenceMonopulseTracker2D
Пакет: поэтапный

Выполните моноимпульсное отслеживание с помощью URA

Синтаксис

ESTANG = step(H,X,STANG)

Описание

Примечание

Начиная с R2016b, вместо использования step метод для выполнения операции, заданной Системной object™, можно вызвать объект с аргументами, как если бы это была функция. Для примера, y = step(obj,x) и y = obj(x) выполнять эквивалентные операции.

ESTANG = step(H,X,STANG) оценивает входящее направление ESTANG входного сигнала, X, на основе первоначального предположения о направлении.

Примечание

Объект выполняет инициализацию при первом выполнении объекта. Эта инициализация блокирует нетронутые свойства и входные спецификации, такие как размерности, сложность и тип данных входных данных. Если вы изменяете свойство nontunable или спецификацию входа, системный объект выдает ошибку. Чтобы изменить нетронутые свойства или входы, необходимо сначала вызвать release метод для разблокировки объекта.

Входные параметры

H

Объект трекера типа phased.SumDifferenceMonopulseTracker2D.

X

Входной сигнал, заданный как вектор-строка, количество столбцов которого соответствует количеству каналов. Можно задать этот аргумент как одинарную или двойную точность.

Размер первой размерности матрицы входа может варьироваться, чтобы симулировать изменяющуюся длину сигнала. Изменение размера может произойти, например, в случае импульсного сигнала с переменной частотой повторения импульса.

STANG

Начальное предположение направления, заданное как вектор 2 на 1 в виде [AzimuthAngle; ElevationAngle] в степенях. Типичным начальным предположением является текущий угол поворота руля. Углы азимута должны быть от -180 до 180. Углы возвышения должны быть между -90 и 90. Углы измеряются в локальной системе координат массива. Для получения дополнительной информации о локальной системе координат URA введите phased.URA.coordinateSystemInfo. Можно задать этот аргумент как одинарную или двойную точность.

Выходные аргументы

ESTANG

Оценка входящего направления, возвращенная как вектор 2 на 1 в форме [AzimuthAngle; ElevationAngle] в степенях. Азимутальные углы находятся между -180 и 180. Углы возвышения находятся между -90 и 90. Углы измеряются в локальной системе координат массива.

Примеры

расширить все

Найдите целевое направление с помощью Sum-Difference 2D Monopulse Tracker

Открыть Live Script

Используя URA, определите направление цели приблизительно при 60 ° азимута и 20 ° повышения.

array = phased.URA('Size',4);
steeringvec = phased.SteeringVector('SensorArray',array);
tracker = phased.SumDifferenceMonopulseTracker2D('SensorArray',array);
x = steeringvec(tracker.OperatingFrequency,[60.1; 19.5]).';
est_dir = tracker(x,[60; 20])

est_dir = 2×1

   60.1000
   19.5000

Алгоритмы

Алгоритм моноимпульса суммы и разности используется для оценки направления прихода узкополосного сигнала, падающего на равномерный линейный массив (ULA). Сначала вычислите обычную реакцию массива, направленной к направлению прибытия φ 0. Для ULA направление прибытия задается широким углом. Чтобы указать, что максимальная ось отклика (MRA) точки к _φ 0 направлению, установите веса равными

$w_{s} = (1, e^{i k d \sin ϕ_{0}}, e^{i k 2 d \sin ϕ_{0}}, \dots, e^{i k (N - 1) d \sin ϕ_{0}})$

где d - интервал между элементами, а k = 2π/λ - число волн. Входящая плоская волна, идущая от любого произвольного φ направления, представлена

$v = (1, e^{i k d \sin ϕ}, e^{i k 2 d \sin ϕ}, \dots, e^{i k (N - 1) d \sin ϕ})$

Обычная реакция этого массива на любую входящую плоскую волну задается как $w_{s}^{H} v (φ)$ и показан на полярном графике ниже как суммарный шаблон. Массив предназначен для направления к φ 0 = 30 °.

Второй шаблон, называемый Difference Pattern, получается при помощи обратных по фазе весов. Веса определяются фазовым обращением второй половины обычного вектора управления. Для массива с четным количеством элементов обратные по фазе веса

$w_{d} = - i (1, e^{i k d \sin ϕ_{0}}, e^{i k 2 d \sin ϕ_{0}}, \dots, e^{i k N / 2 d \sin ϕ_{0}}, - e^{i k (N / 2 + 1) d \sin ϕ_{0}}, \dots, - e^{i k (N - 1) d \sin ϕ_{0}})$

(Для массива с нечетным количеством элементов средний вес устанавливается равным нулю). Мультипликативный коэффициент –i используется для удобства. Ответ массива различия на входящий вектор

$w_{d}^{H} v (φ)$

Этот рисунок показывает суммарные и разностные диаграммы направленности четырёхэлементного равномерного линейного массива (ULA), направленной на 30 ° с широкой стороны. Элементы массива разнесены на половину длины волны. Суммарный шаблон показывает, что массив имеет максимальную характеристику на уровне 30 °, а разностный шаблон имеет значение null на уровне 30 °.

Кривая моноимпульсной характеристики получается путем деления шаблона различия на суммарный шаблон и взятия действительной части.

$R (φ) = R e (\frac{w_{d}^{H} v (φ)}{w_{s}^{H} v (φ)})$

Чтобы использовать кривую моноимпульсной характеристики, чтобы получить угол прихода, φ, узкополосного сигнала, x, compute

$z = R e (\frac{w_{d}^{H} x}{w_{s}^{H} x})$

и инвертируйте кривую отклика,^-1(z), для получения φ.

Кривая отклика, как правило, не является одинарной и может быть инвертирована только тогда, когда углы прихода лежат в пределах основной лепестка, где она является одинарной. Этот рисунок показывает кривую моноимпульсной характеристики в пределах основной лепестка четырехэлементной массива ULA.

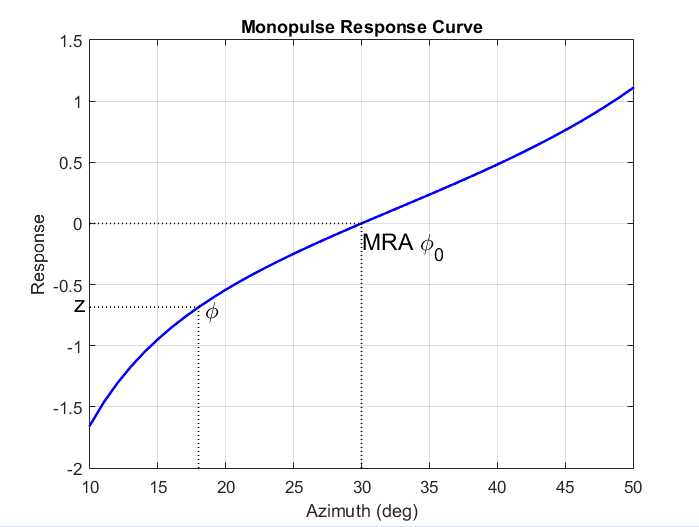
Существует два желательных свойства кривой моноимпульсной характеристики. Первый - это то, что он имеет крутой уклон. Крутой уклон страхует робастность от шума. Второе свойство состоит в том, что майнлобе быть максимально широким. Крутой склон обеспечивается большим массивом, но приводит к меньшему мундиру. Вам нужно будет обмениваться одним свойством с другой.

Для получения дополнительной информации см. раздел [1].

Ссылки

[1] Seliktar, Y. Space-Time Adaptive Monopulse Processing. Доктор философии. Дипломная работа. Технологический институт Джорджии, Атланта, 1998 год.

[2] Родос, Д. Введение в моноимпульс. Dedham, MA: Artech House, 1980.

См. также

azel2phitheta | azel2uv | phitheta2azel | uv2azel

Документация