Определение числовой жесткости вашей модели помогает вам решить между использованием неявного или явного решателя с фиксированным шагом для симуляции в реальном времени. Чтобы определить числовую жесткость, сначала используйте рабочий процесс подготовки модели реального времени, чтобы оптимизировать скорость и точность вашей модели. Затем симулируйте свою модель с помощью как явных, так и неявных решателей с фиксированным шагом. Сравните результаты симуляции, чтобы увидеть, как ведут себя решатели. Если ваша модель численно жесткая, явный решатель обычно показывает небольшие колебания вокруг желаемого решения.
Неявные решатели более устойчивы, чем явные решатели, однако явные решатели быстрее. Для устойчивых результатов при выполнении симуляции в реальном времени с численно жесткой моделью используйте неявный решатель с фиксированным шагом. Если ваша модель не жесткая, используйте явный решатель, чтобы максимизировать скорость симуляции.
В этом примере вы получаете результаты ссылки путем симуляции пневматической модели с решателем с переменным шагом. Вы также конфигурируете и симулируете модель с помощью неявного, а затем явного глобального Simulink с фиксированным шагом® решатель. Затем вы сравните результаты всех трех симуляций, чтобы определить, является ли пневматическая модель численно жесткой.
Чтобы открыть модель, в MATLAB® в командной строке введите:
ssc_pneumatic_rts_reference
Сохраните модель как stiffness_model в папку с возможностью записи в пути MATLAB.
Симулируйте модель.
Присвойте результаты симуляции новым переменным.
yRef = yout; tRef = tout;
Постройте график результатов симуляции переменного шага.
h1 = figure;
plot(tRef,yRef)
h1Leg = legend({'Reference'});
title('Speed')
xlabel('Time (s)')
ylabel('Speed (rpm)')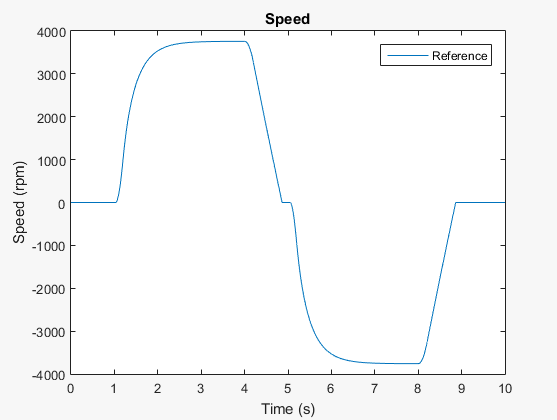
Сконфигурируйте модель для симуляции с фиксированным шагом с неявным решателем ode14x. На панели параметров конфигурации Solver установите:
Type с Fixed-step
Solver с ode14x (extrapolation)
В разделе Additional options Fixed-step size (fundamental sample time) для 1e-3
Number of Newton's iterations с 1.
Нажмите Apply.
Симулируйте модель.
Присвойте результаты симуляции новым переменным.
yOde14x = yout; tOde14x = tout;
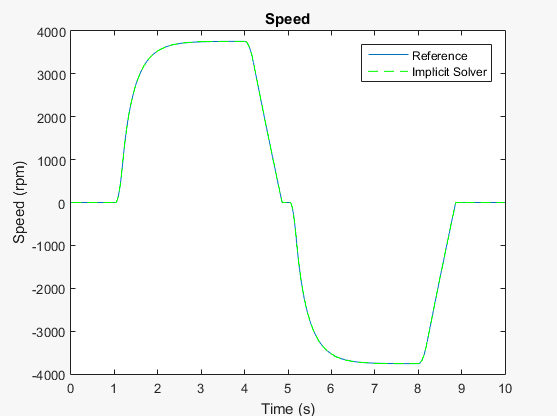
Используйте stairs функция для построения графика результатов неявной симуляции с фиксированным шагом, чтобы можно было увидеть, как ведет себя решатель, когда он выполняет каждый шаг в симуляции.
h1 hold on stairs(tOde14x,yOde14x,'g--') h1Leg = legend({'Reference','Implicit Solver'});
Результаты выглядят одинаково.
Сконфигурируйте модель для симуляции с фиксированным шагом с явным решателем с фиксированным шагом ode5. На панели параметров конфигурации Solver установите:
Type с Fixed-step
Solver с ode5 (Dormand-Prince)
Нажмите OK.
Пропустите входной сигнал, чтобы предоставить необходимую входную производную для явного решателя. В диалоговом окне блока PS-S Simulink Converter на вкладке Input Handling установите Filtering and derivatives Filter Input. Нажмите OK.
Симулируйте модель.
Присвойте результаты симуляции новым переменным.
yOde5 = yout; tOde5 = tout;
Используйте stairs функция для построения графика результатов явной симуляции с фиксированным шагом.
h1 hold on stairs(tOde5,yOde5,'r-') h1Leg = legend({'Reference','Implicit Solver','Explicit Solver'});
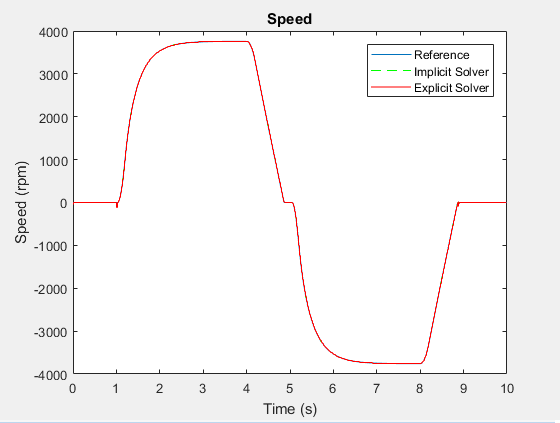
Результаты различаются в точках перегиба.
Чтобы увидеть результаты более близко, увеличьте изображение точки перегиба сразу после времени t = ~ 1 секунду.
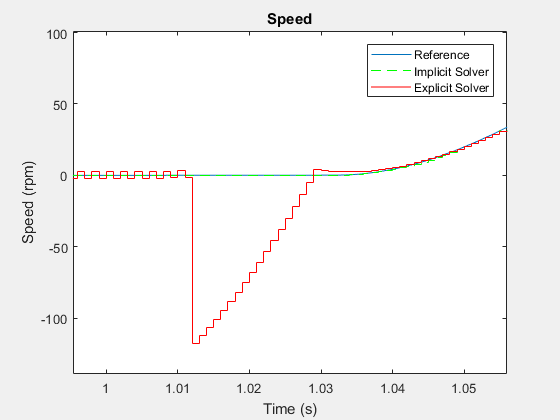
Неявный решатель следует по пути, который похож на путь, который принимает решатель переменного шага при генерации результатов ссылки. Колебания, которые показывает явный решатель, указывают, что модель численно жесткая. Колебания также указывают, что явный решатель является более в вычислительном отношении дорогим, чем неявный решатель для симуляции жесткой модели. Используйте глобальный или локальный неявный решатель с фиксированным шагом для симуляции в реальном времени с численно жесткими моделями, чтобы избежать ненужных вычислительных затрат.