Этот пример помогает вам выполнить шаги, описанные в рабочем процессе подготовки модели реального времени, и достичь целей, описанных в целях подготовки модели.
В Determine Step Size вы используете результаты симуляции переменных шагов вашей модели Simscape™, чтобы идентифицировать, когда размер шага уменьшается, чтобы точно захватывать поведение при разрывах и для быстрой динамики в численно жестких системах. Эти типы событий часто требуют, чтобы решатели предприняли шаги, которые являются слишком маленькими, чтобы поддерживать симуляцию в реальном времени. В этом примере показано, как использовать результаты определения размера шага для идентификации численно жесткого элемента в модели. Это также показывает, как изменить элемент для более быстрой симуляции, не жертвуя точностью.
Численная жесткость может помешать вашей модели быть способной в реальном времени. Модель с поддержкой реального времени является такой, которая дает приемлемые результаты, не принимая переполнения, когда вы моделируете его на целевом процессоре. Жесткие системы содержат динамику, которая изменяется как быстро, так и медленно. Когда решатели делают большие шаги, они обычно захватывают медленно изменяющуюся динамику, но они, как правило, пропускают быстрые изменения, если они не делают небольшие шаги. Небольшие шаги вызывают переполнение, когда они не обеспечивают достаточное время для компьютера в реальном времени, чтобы выполнить вычислительные решения за один шаг.
Чтобы вы уменьшили числовую жесткость, вы устраняете быстрые изменения. Если быстрых изменений нет, решатель может сделать большие шаги и все равно получить точные результаты симуляции. Чем больше размер шага, тем меньше вероятность того, что ваша модель генерирует переполнение во время симуляции в реальном времени.
Чтобы открыть модель, в MATLAB® в командной строке введите:
model = 'ssc_pneumatic_rts_reference';
open_system(model)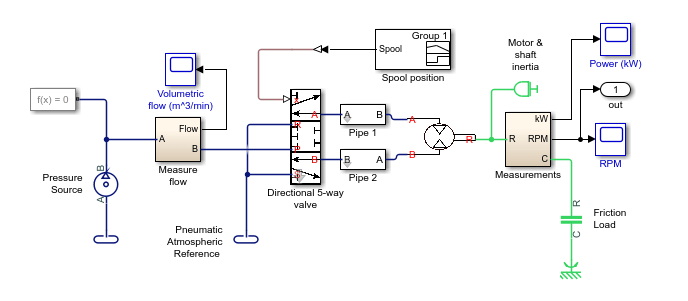
Симулируйте модель:
sim(model)
Создайте рисунок, которая содержит семилогарифмический график размера шага решателя, график результатов скорости двигателя и график результатов потока газа.
h1 = figure; subplot(3,1,1) semilogy(tout(1:end-1),diff(tout),'-x') title('Solver Step Size and Results') ylabel('Step Size (s)') subplot(3,1,2) plot(tout,Pneu_rts_RPM_DATA.signals.values) ylabel('Speed (rpms)') subplot(3,1,3) plot(tout,Pneu_rts_Vol_Flow_DATA.signals.values) xlabel('Time (s)') ylabel('Flow Rate (m^3/min)')
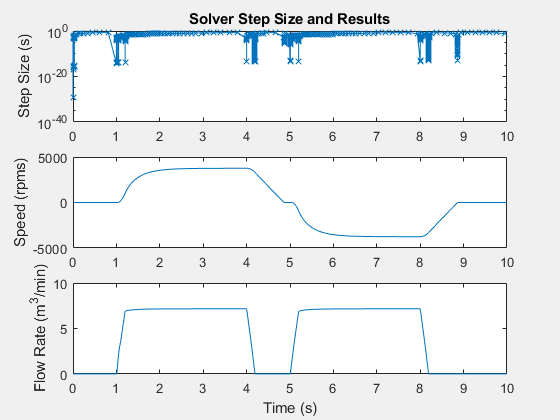
Симуляция занимает шаги меньше 1e-10 секунд, когда:
Скорость двигателя около нуля об/мин (время симуляции t = ~ 1, 5 и 9 секунд)
Изменение скорости двигателя инициируется с установившейся скорости на новую (время t = ~ 4 и 8 секунд)
Изменение скорости потока жидкости инициируется с установившейся скорости на новую скорость потока жидкости (время t = ~ 4 и 8 секунд)
Объемный расход около нуля м ^ 3/мин (t = ~ 1, 4 и 5 секунд)
Результаты показывают, что размеры небольшого шага требуются для достижения точности, когда симуляция захватывает динамику, которая включает трение или небольшие сжимаемые объемы. Элементы, которые генерируют пересечения нуля, могут также нести ответственность за небольшие шаги и медленное время восстановления.
Присвойте результаты симуляции новым переменным в рабочем пространстве MATLAB, чтобы можно было сравнить данные с результатами изменяемой модели.
timeRef = tout; simlogRef = simlog;
Исследуйте фрикционную нагрузку в модели, чтобы определить, включает ли она разрывы или имеет небольшую временную константу, которая вызывает числовую жесткость. Измените элемент, если он вызывает быстро изменяющуюся динамику, требующую небольшого размера шага.
Сохраните модель как rts_stiffness_model в папке с возможностью записи в пути MATLAB.
Откройте диалоговое окно блока Triction Load, блок Rotational Friction. Рисунок показывает характеристику крутящего момента трения/относительной скорости для простого приближения непрерывного трения, которое моделирует блок.
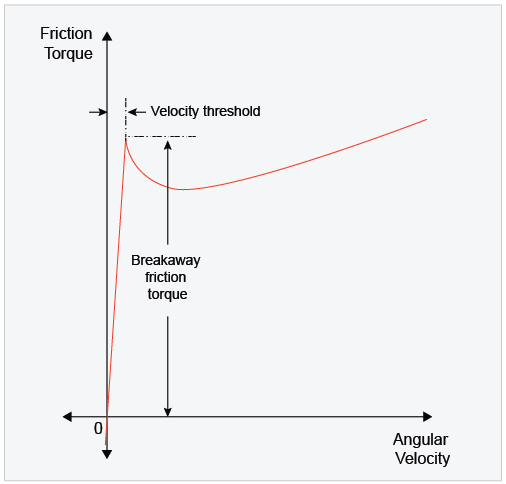
Крутящий момент отхода моделируется как функция от порога скорости. Когда скорость близка к нулю, небольшое изменение скорости приводит к большому изменению крутящего момента. Когда скорость не близка к нулю, изменение крутящего момента является более постепенным. Этот блок представляет жесткий элемент. Чтобы сделать элемент менее жестким, задайте более высокое значение для Breakaway friction velocity.
На вкладке Parameters диалогового окна измените Breakaway friction velocity на 0.059137 на 0.1 рад/с.
Симулируйте измененную модель.
Чтобы увидеть, как изменение порога скорости для блока трения влияет на жесткость компонента, сравните размеры шагов для этих двух симуляций. Эталонные результаты отвечают ожиданиям, основанным на эмпирических и теоретических данных. Можно оценить точность измененной модели путем сравнения результатов скорости от измененной модели с результатами от исходной версии модели.
Постройте график размера шага для результатов ссылки для измененной модели на рисунке, который содержит ссылочные данные.
h2 = figure; semilogy(timeRef(1:end-1),diff(timeRef),'-x',... 'LineWidth',1,'MarkerSize',7) hold on semilogy(tout(1:end-1),diff(tout),'--x','Color','r',... 'LineWidth',.1,'MarkerSize',5) title('Solver Step Size') xlabel('Time (s)') ylabel('Step Size (s)') h1Leg = legend({'Reference','Modified'},'Location','best');

Размер шага быстрее восстанавливается из события, которое происходит во время симуляции t = 4 и 9 секунд. Симуляция в эти моменты менее жесткая.
Извлеките данные о скорости и времени из узлов регистрации для исходных и измененных моделей.
speedRefNode = simlogRef.Measurements.Ideal_Rotational_Motion_Sensor.R.w; speedRef = speedRefNode.series.values('rpm'); timeRef = speedRefNode.series.time; speedModNode = simlog.Measurements.Ideal_Rotational_Motion_Sensor.R.w; speedMod = speedModNode.series.values('rpm'); timeMod = speedModNode.series.time;
Постройте и сравните результаты для данных о скорости для обоих симуляций, чтобы убедиться, что измененная модель точна.
h3 = figure; plot(timeRef,speedRef) h3; hold on plot(timeMod,speedMod,'r--') title('Speed') xlabel('Time (s)') ylabel('Speed (rpms)') h3Leg = legend({'Reference','Modified'},'Location','best');
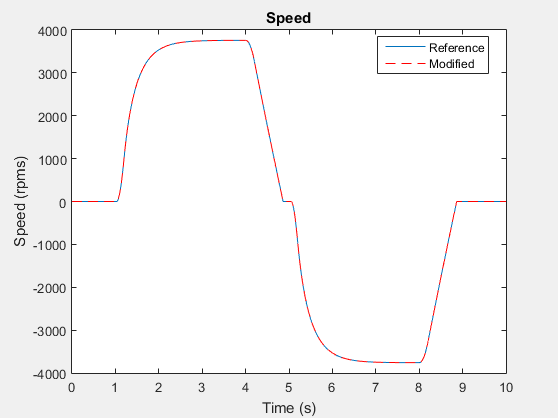
Увеличьте изображение для более близкого взгляда на точку перегиба в момент (t) = ~ 5 секунд.
h3; xStart = 0; xEnd = 10; yStart = -4000; yEnd = 4000; xZoomStart1 = 4.8; xZoomEnd1 = 5.2; yZoomStart1 = -400; yZoomEnd1 = 150; axis([xZoomStart1 xZoomEnd1 yZoomStart1 yZoomEnd1])
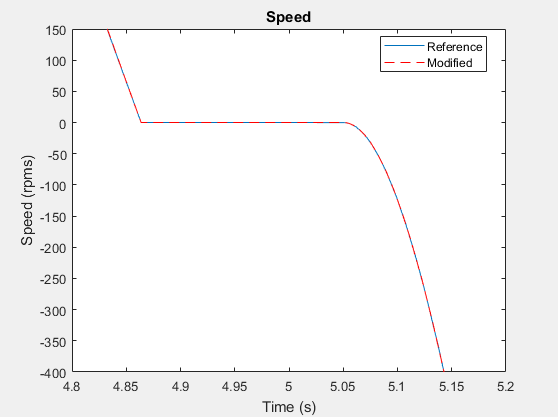
На этом уровне масштаба можно увидеть, что результаты симуляции для измененной модели достаточно точны, чтобы соответствовать ожиданиям на основе эмпирических и теоретических данных.
Фрикционная нагрузка теперь менее численно жесткая. Рисунок размера шага во время симуляции показывает, что другие элементы модели также ответственны за медленное время восстановления. Уменьшите более медленные шаги восстановления, исследуя и изменяя другие элементы, которые вызывают жесткость.
Можно также увеличить скорость путем изменения модели с помощью методов в Уменьшить вычислительные затраты и Уменьшить пересечения нуля. Если можно исключить все небольшие шаги, которые могут сгенерировать переполнение, можно попытаться запустить симуляцию с фиксированным шагом с помощью методов, показанных в Выборе размера шага и количества итераций.