Модель линии

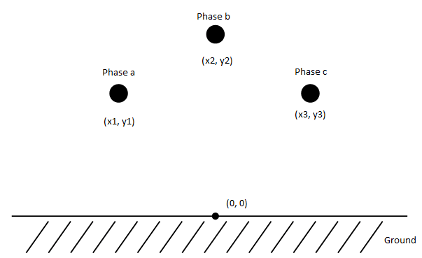
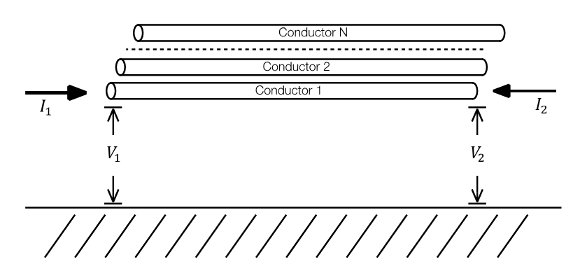
Электромагнитное поведение мультипроводниковой линии электропередачи описывается уравнением телеграфиста.

Где:

Это общие решения для вектора токов и напряжений.

$I\left(x\right)=e^{-\text{Ψ}x}{C}_1+e^{\text{Ψ}x}{C}_2$

(1)

$Y_{c}V\left(x\right)= e^{-\text{Ψ}x}{C}_1-e^{\text{Ψ}x}{C}_2$

(2)

Где $$\text{Ψ}=\sqrt{YZ}$$ является матрицей распространения и $Y_c={(\sqrt{YZ})}^{-1}Y$ - допустимость характеристики.

Рассмотрим теперь сегмент линии электропередачи длины x = l. В начале одного из его концов, когда x = 0, уравнения 1 и 2 оцениваются следующим образом.

$I_1=C_1+C_2$

(3)

$Y_c{V}_1= C_1-C_2$

(4)

Интегрированные постоянные векторы _C1 и _C2 могут быть выражены в терминах _I0 и _V0.

$C_1=\frac{(I_1+Y_c{V}_1)}{2}$

(5)

$C_2=\frac{(I_1-Y_c{V}_1)}{2}$

(6)

Точно так же при x = l уравнения 1 и 2 оцениваются следующим образом.

$I_2=e^{-\Psi \text{l}}{C}_1+e^{\Psi \text{l}}{C}_2$

(7)

$Y_c{V}_2=e^{-\Psi \text{l}}{C}_1-e^{\Psi \text{l}}{C}_2$

(8)

Чтобы получить два фундаментальных уравнения для модели линии электропередачи, сначала вы используете уравнения 7 и 8, чтобы выполнить это вычисление.

$I_2-Y_c{V}_2=-2e^{-\Psi l}{C}_1$

(9)

Тогда вы подставляете уравнение 5 в уравнение 9.

$I_2-Y_c{V}_2=-H(I_1+Y_c{V}_1)$

(10)

Где $H=e^{-\text{Ψ}l}$ - матрица коэффициента распространения. Уравнение 10 устанавливает отношение между напряжениями и токами на выводах многопроводной секции линии.

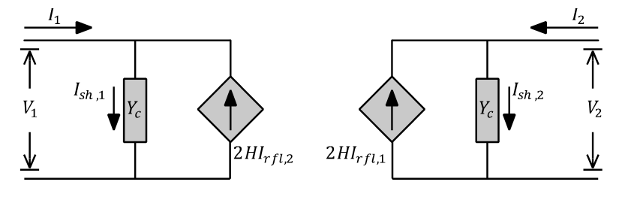
Можно получить сопутствующее выражение, обеспечивающее модель для терминала 1 при x = 0.

$I_1-Y_c{V}_1=-H(I_2+Y_c{V}_2)$

(11)

Определите:

И, наконец, переписать уравнения 10 и 11 следующим образом:

Эти уравнения составляют модель линии бегущей волны для сегмента длины L.

В частности, для линий электропередачи с возвратом земли, параметры сильно зависят от частоты. Затем моделирующие решения выполняются непосредственно в фазовой области. Блок автоматически вычисляет импеданс и матрицы допуска характеристики во всей частотной области значений, выполняя приближение через рациональный подбор кривой.

Рациональный подбор кривой для этой модели выполняется с помощью процедуры вектора fitting (VF). Для получения дополнительной информации о модели линии фазы области и анализе пространства состояний, смотрите Реализацию модели широкополосной линии в Matlab для анализа EMT [1].