PMSM (Six-Phase)

Шестифазный синхронный двигатель с постоянными магнитами с синусоидальным распределением потока

Библиотека:
Simscape/Электрический/Электромеханический/Постоянный магнит

Описание

Блок PMSM (Six-Phase) моделирует синхронную машину с постоянными магнитами (PMSM) с шестифазным статором со звездной обмоткой.

Шестифазный PMSM имеет две группы трехфазных обмоток статора: группу ABC и группу XYZ. Эти две группы имеют 30 степени фазовый сдвиг.

Рисунок показывает эквивалентную электрическую схему для обмоток статора.

Уравнения

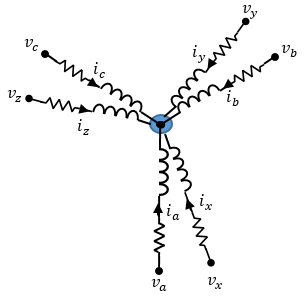
Напряжения на обмотках статора определяются:

$[\begin{array}{l} v_{a} \\ v_{b} \\ v_{c} \\ v_{x} \\ v_{y} \\ v_{z} \end{array}] = [\begin{matrix} R_{s} & 0 & 0 & 0 & 0 & 0 \\ 0 & R_{s} & 0 & 0 & 0 & 0 \\ 0 & 0 & R_{s} & 0 & 0 & 0 \\ 0 & 0 & 0 & R_{s} & 0 & 0 \\ 0 & 0 & 0 & 0 & R_{s} & 0 \\ 0 & 0 & 0 & 0 & 0 & R_{s} \end{matrix}] [\begin{array}{l} i_{a} \\ i_{b} \\ i_{c} \\ i_{x} \\ i_{y} \\ i_{z} \end{array}] + [\begin{array}{l} \frac{d ψ_{a}}{d t} \\ \frac{d ψ_{b}}{d t} \\ \frac{d ψ_{c}}{d t} \\ \frac{d ψ_{x}}{d t} \\ \frac{d ψ_{y}}{d t} \\ \frac{d ψ_{z}}{d t} \end{array}],$

где:

_va, _vb и _vc являются отдельными напряжениями фазы от порта ~ABC до нейтрального порта n1.
_vx, _vy и _vz являются отдельными напряжениями фазы от порта ~XYZ до нейтрального порта n2.
_Rs - эквивалентное сопротивление каждой обмотки статора.
_ia, _ib и _ic являются токами, протекающими от порта ~ABC к порту n1.
_ix, _iy и _iz являются токами, протекающими от порта ~XYZ к порту n2.
$\frac{d ψ_{a}}{d t},$ $\frac{d ψ_{b}}{d t},$ $\frac{d ψ_{c}}{d t}$ $\frac{d ψ_{x}}{d t},$ $\frac{d ψ_{y}}{d t},$ и $\frac{d ψ_{z}}{d t}$ - скорости изменения магнитного потока в каждой обмотке статора.

Постоянный магнит и шесть обмоток способствуют общему потоку, связывающему каждую обмотку. Общий поток определяется:

$[\begin{array}{l} ψ_{a} \\ ψ_{b} \\ ψ_{c} \\ ψ_{x} \\ ψ_{y} \\ ψ_{z} \end{array}] = [\begin{matrix} L_{a a} & L_{a b} & L_{a c} & L_{a x} & L_{a y} & L_{a z} \\ L_{b a} & L_{b b} & L_{b c} & L_{b x} & L_{b y} & L_{b z} \\ L_{c a} & L_{c b} & L_{c c} & L_{c x} & L_{c y} & L_{c z} \\ L_{x a} & L_{x b} & L_{x c} & L_{x x} & L_{x y} & L_{x z} \\ L_{y a} & L_{y b} & L_{y c} & L_{y x} & L_{y y} & L_{y z} \\ L_{z a} & L_{z b} & L_{z c} & L_{z x} & L_{z y} & L_{z z} \end{matrix}] [\begin{array}{l} i_{a} \\ i_{b} \\ i_{c} \\ i_{x} \\ i_{y} \\ i_{z} \end{array}] + [\begin{array}{l} ψ_{a m} \\ ψ_{b m} \\ ψ_{c m} \\ ψ_{x m} \\ ψ_{y m} \\ ψ_{z m} \end{array}],$

где:

_ψa, _ψb, _ψc, _ψx, _ψy, и _ψz являются полными потоками, которые связывают каждую обмотку статора.
_Laa, _Lbb, _Lcc, _Lxx, _Lyy, и _Lzz являются самоиндукциями обмоток статора.
_Lab, _Lac, _Lba и так далее являются взаимными индуктивностями обмоток статора.
_ψam, _ψbm, _ψcm, _ψxm, _ψym, и _ψzm являются потоками постоянного магнита, связывающими обмотки статора.

Индуктивности в обмотках статора являются функциями электрического угла ротора, заданными как:

$θ_{e} = N θ_{r} + r o t o r o f f s e t$

$\begin{array}{l} L_{a a} = L_{s} + L_{m} потому что (2 θ_{e}) \\ L_{b b} = L_{s} + L_{m} потому что (2 (θ_{e} - 2 \frac{π}{3})) \\ L_{c c} = L_{s} + L_{m} потому что (2 (θ_{e} + 2 \frac{π}{3})) \\ L_{x x} = L_{s} + L_{m} потому что (2 (θ_{e} - \frac{π}{6})) \\ L_{y y} = L_{s} + L_{m} потому что (2 (θ_{e} - 5 \frac{π}{6})) \\ L_{z z} = L_{s} + L_{m} потому что (2 (θ_{e} + \frac{π}{2})) \\ L_{a b} = L_{b a} = - M_{s} - L_{m} (2cos (θ_{e} + \frac{π}{6})) \\ L_{b c} = L_{c b} = - M_{s} - L_{m} \cos (2 (θ_{e} + \frac{π}{6} - 2 \frac{π}{3})) \\ L_{c a} = L_{a c} = - M_{s} - L_{m} потому что (θ_{e} + \frac{π}{6} + 2 \frac{π}{3}) \\ L_{x y} = L_{y x} = - M_{s} - L_{m} \cos (2 θ_{e}) \\ L_{y z} = L_{z y} = - M_{s} - L_{m} потому что (2 (θ_{e} - 2 \frac{π}{3})) \\ L_{z x} = L_{x z} = - M_{s} - L_{m} потому что (2 (θ_{e} + 2 \frac{π}{3})) \\ L_{a x} = L_{x a} = \sqrt{3} M_{s} + L_{m} потому что (2 (θ_{e} - \frac{π}{12})) \\ L_{a y} = L_{y a} = - \sqrt{3} M_{s} + L_{m} потому что (2 (θ_{e} - 5 \frac{π}{12})) \\ L_{a z} = L_{z a} = L_{m} потому что (2 (θ_{e} + \frac{π}{4})) \\ L_{b x} = L_{x b} = L_{m} потому что (2 (θ_{e} - 5 \frac{π}{12})) \\ L_{b y} = L_{y b} = \sqrt{3} M_{s} + L_{m} потому что (2 (θ_{e} + \frac{π}{4})) \\ L_{b z} = L_{z b} = - \sqrt{3} M_{s} + L_{m} потому что (2 (θ_{e} - \frac{π}{12})) \\ L_{c x} = L_{x c} = - \sqrt{3} M_{s} + L_{m} потому что (2 (θ_{e} + \frac{π}{4})) \\ L_{c y} = L_{y c} = L_{m} потому что (2 (θ_{e} - \frac{π}{12})) \\ L_{c z} = L_{z c} = \sqrt{3} M_{s} + L_{m} потому что (2 (θ_{e} - 5 \frac{π}{12})) \end{array}$

где:

_θr - механический угол ротора.
_θe - электрический угол ротора.
rotor offset 0 если вы задаете электрический угол ротора относительно оси d, или -pi/2 если задан электрический угол ротора относительно оси q.
_Ls является самоиндуктивностью статора на фазу. Это значение является средней индуктивностью каждой из обмоток статора.
_Lm - индуктивность статора. Это значение является колебанием самоиндуктивности и взаимной индуктивности с изменением угла ротора.
_Ms является взаимной индуктивностью статора. Это значение является средней взаимной индуктивностью между обмотками статора.

Обмотка связи с постоянными магнитами a-a' на максимуме, когда _θe = 0 ° и нули, когда _θe = 90 °. Поэтому связанный поток мотора определяется:

$[\begin{array}{l} ψ_{a m} \\ ψ_{b m} \\ ψ_{c m} \\ ψ_{x m} \\ ψ_{y m} \\ ψ_{z m} \end{array}] = [\begin{array}{l} ψ_{m} \cos θ_{e} \\ ψ_{m} \cos (θ_{e} - 2 π / 3) \\ ψ_{m} \cos (θ_{e} + 2 π / 3) \\ ψ_{m} \cos (θ_{e} - π / 6) \\ ψ_{m} \cos (θ_{e} - 5 π / 6) \\ ψ_{m} c o s (θ_{e} + π / 2) \end{array}],$

где _ψm - редактирование потока постоянных магнитов.

Упрощенные электрические уравнения

Применение развязанного преобразования к электрическим уравнениям блока создает выражение для крутящего момента, которое не зависит от угла ротора.

Развязанное преобразование определяется:

$P (θ_{e}) = \frac{1}{3} [\begin{matrix} \cos θ_{e} & \cos (θ_{e} - 2 \frac{π}{3}) & \cos (θ_{e} + 2 \frac{π}{3}) & c o s (θ_{e} - \frac{π}{6}) & \cos (θ_{e} - 5 \frac{π}{6}) & \cos (θ_{e} + \frac{π}{2}) \\ - \sin θ_{e} & - \sin (θ_{e} - 2 \frac{π}{3}) & - \sin (θ_{e} + 2 \frac{π}{3}) & - \sin (θ_{e} - \frac{π}{6}) & - \sin (θ_{e} - 5 \frac{π}{6}) & - \sin (θ_{e} + \frac{π}{2}) \\ 1 & - \frac{1}{2} & - \frac{1}{2} & - \frac{\sqrt{3}}{2} & \frac{\sqrt{3}}{2} & 0 \\ 0 & - \frac{\sqrt{3}}{2} & \frac{\sqrt{3}}{2} & \frac{1}{2} & \frac{1}{2} & - 1 \\ 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 \end{matrix}] .$

Матрица преобразования, P, имеет это псевдоортогональное свойство:

$P^{- 1} (θ_{e}) = 3 P^{T} (θ_{e}) .$

Использование развязанного преобразования на напряжениях и токах обмотки статора преобразует их в dq0 систему координат, которая не зависит от угла ротора.

Чтобы получить d-ось, q-ось и напряжения статора с нулевой последовательностью и потокосцепления для групп ABC и XYZ, примените преобразование к уравнениям потокосцепления напряжения и потока:

$[\begin{array}{l} v_{d} \\ v_{q} \\ v_{z 1} \\ v_{z 2} \\ v_{01} \\ v_{02} \end{array}] = [\begin{matrix} R_{s} & 0 & 0 & 0 & 0 & 0 \\ 0 & R_{s} & 0 & 0 & 0 & 0 \\ 0 & 0 & R_{s} & 0 & 0 & 0 \\ 0 & 0 & 0 & R_{s} & 0 & 0 \\ 0 & 0 & 0 & 0 & R_{s} & 0 \\ 0 & 0 & 0 & 0 & 0 & R_{s} \end{matrix}] [\begin{array}{l} i_{d} \\ i_{q} \\ i_{z 1} \\ i_{z 2} \\ i_{01} \\ i_{02} \end{array}] + [\begin{matrix} - ψ_{q} \\ ψ_{d} \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix}] N ω + \frac{d}{d t} [\begin{matrix} ψ_{d} \\ ψ_{q} \\ ψ_{z 1} \\ ψ_{z 2} \\ ψ_{01} \\ ψ_{02} \end{matrix}]$

$[\begin{matrix} ψ_{d} \\ ψ_{q} \\ ψ_{z 1} \\ ψ_{z 2} \\ ψ_{01} \\ ψ_{02} \end{matrix}] = [\begin{matrix} L_{d} & 0 & 0 & 0 & 0 & 0 \\ 0 & L_{q} & 0 & 0 & 0 & 0 \\ 0 & 0 & L_{0} & 0 & 0 & 0 \\ 0 & 0 & 0 & L_{0} & 0 & 0 \\ 0 & 0 & 0 & 0 & L_{0} & 0 \\ 0 & 0 & 0 & 0 & 0 & L_{0} \end{matrix}] [\begin{array}{l} i_{d} \\ i_{q} \\ i_{z 1} \\ i_{z 2} \\ i_{01} \\ i_{02} \end{array}] + [\begin{matrix} ψ_{m} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix}]$

где:

_vd, _vq, _vz1, _vz2, _v01, и _v02 d, q, z1, и z2 компоненты и напряжения статора нулевой последовательности для ABC и групп XYZ, определенных:

$[\begin{array}{l} v_{d} \\ v_{q} \\ v_{z 1} \\ v_{z 2} \\ v_{01} \\ v_{02} \end{array}] = P [\begin{array}{l} v_{a} \\ v_{b} \\ v_{c} \\ v_{x} \\ v_{y} \\ v_{z} \end{array}] .$
_id, _iq, _iz1, _iz2, _i01, и _i02 d - ось, q - ось и ток статора нулевой последовательности для ABC и групп XYZ, определенных:

$[\begin{array}{l} i_{d} \\ i_{q} \\ i_{z 1} \\ i_{z 2} \\ i_{01} \\ i_{02} \end{array}] = P [\begin{array}{l} i_{a} \\ i_{b} \\ i_{c} \\ i_{x} \\ i_{y} \\ i_{z} \end{array}] .$
$L_{d} = L_{s} + 4 M_{s} + 3 L_{m}$ - индуктивность d оси статора.
$L_{q} = L_{s} + 4 M_{s} - 3 L_{m}$ - индуктивность q оси статора.
$L_{0} = L_{s} - 2 M_{s}$ - индуктивность нулевой последовательности статора.
ω - механическая скорость вращения ротора.
N - количество пар полюсов постоянных магнитов ротора.

Уравнение крутящего момента определяется:

$T = 3 N [i_{q} (i_{d} L_{d} + ψ_{m}) - i_{d} i_{q} L_{q}] .$

Переменные

Используйте настройки Variables, чтобы задать приоритет и начальные целевые значения для основных переменных перед симуляцией. Для получения дополнительной информации смотрите Задать приоритет и Начальный целевой объект для основных переменных.

Порты

Сохранение

расширить все

`~ABC` - Обмотки ABC статора
электрический

Трехфазный электрический порт, сопоставленный с обмотками ABC статора.

`~XYZ` - Обмотки XYZ статора
электрический

Трехфазный электрический порт, сопоставленный с обмотками XYZ статора.

`n1` - нейтральная точка обмотки ABC
электрический

Электрический порт сопоставлен с нейтральной точкой строения обмотки ABC.

Зависимости

Чтобы включить этот порт, установите Zero sequence равным Include.

`n2` - нейтральная точка обмотки XYZ
электрический

Электрический порт сопоставлен с нейтральной точкой строения обмотки XYZ.

Зависимости

Чтобы включить этот порт, установите Zero sequence равным Include.

`R` - Ротор мотора
механический вращательный

Механический вращательный порт сопоставлен с ротором мотора.

`C` - Корпус мотора
механический вращательный

Механический вращательный порт сопоставлен с корпусом мотора.

Параметры

расширить все

Главный

`Number of pole pairs` - Количество пар полюсов
`6` (по умолчанию) | скаляром

Количество пар полюсов постоянных магнитов на роторе.

`Permanent magnet flux linkage parameterization` - Параметризация потокосцепления с постоянными магнитами
`Specify flux linkage` (по умолчанию) | `Specify torque constant` | `Specify back EMF constant`

Редактирование с постоянными магнитами, заданное как Specify flux linkage, Specify torque constant, или Specify back EMF constant.

`Permanent magnet flux linkage` - редактирование с постоянными магнитами
`0.03` `Wb` (по умолчанию) | скаляром

Пик потока постоянных магнитов, редактирования с любой из обмоток статора.

Зависимости

Чтобы включить этот параметр, установите Permanent magnet flux linkage parameterization равным Specify flux linkage.

`Torque constant` - Крутящий момент константа
`0.18` `N*m/A` (по умолчанию) | скаляром

Крутящий момент, константа для любой из обмоток статора.

Зависимости

Чтобы включить этот параметр, установите Permanent magnet flux linkage parameterization равным Specify torque constant.

`Back EMF constant` - Коэффициент противо-ЭДС, постоянная
`0.18` `V/(rad/s)` (по умолчанию) | скаляром

Коэффициент противо-ЭДС, постоянная с любой из обмоток статора.

Зависимости

Чтобы включить этот параметр, установите Permanent magnet flux linkage parameterization равным Specify back EMF constant.

`Stator parameterization` - Параметризация статора
`Specify Ld, Lq, and L0` (по умолчанию) | `Specify Ls, Lm, and Ms`

Параметризация статора, заданная как Specify Ld, Lq, and L0 или Specify Ls, Lm, and Ms.

`Stator d-axis inductance, Ld` - Индуктивность d статора
`0.00019` `H` (по умолчанию) | скаляром

d индуктивность оси.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization равным Specify Ld, Lq, and L0.

`Stator q-axis inductance, Lq` - Индуктивность q статора
`0.00025` `H` (по умолчанию) | скаляром

q индуктивность оси .

Зависимости

Чтобы включить этот параметр, установите Stator parameterization равным Specify Ld, Lq, and L0.

`Stator zero-sequence inductance, L0` - Индуктивность нулевой последовательности статора
`0.00016` `H` (по умолчанию) | скаляром

Индуктивность нулевой последовательности.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization равным Specify Ld, Lq, and L0.

`Stator self-inductance per phase, Ls` - Самоиндуктивность статора на фазу
`0.0002` `H` (по умолчанию) | скаляром

Средняя индуктивность каждой из пяти обмоток статора.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization равным Specify Ls, Lm, and Ms.

`Stator inductance fluctuation, Lm` - Колебания индуктивности статора
`-0.00002` `H` (по умолчанию) | скаляром

Колебания самоиндуктивности и взаимной индуктивности обмоток статора с углом ротора.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization равным Specify Ls, Lm, and Ms.

`Stator mutual inductance, Ms` - Взаимная индуктивность статора
`0.00002` `H` (по умолчанию) | скаляром

Средняя взаимная индуктивность между обмотками статора.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization равным Specify Ls, Lm, and Ms.

`Stator resistance per phase, Rs` - Сопротивление статора на фазу
`0.013` `Ohm` (по умолчанию) | скаляром

Сопротивление каждой из обмоток статора.

`Zero sequence` - Опция нулевой последовательности
`Include` (по умолчанию) | `Exclude`

Следует ли включать или исключать условия нулевой последовательности.

Include - Включите условия нулевой последовательности. Чтобы расставить приоритеты для точности модели, используйте эту настройку по умолчанию. Использование этой опции приводит к ошибке для симуляций, которые используют решатель Секционирования. Для получения дополнительной информации смотрите Увеличение скорости симуляции с помощью решателя секционирования.
Exclude - Исключить условия нулевой последовательности. Чтобы определить приоритеты скорости симуляции для симуляции рабочего стола или развертывания приложений, выберите эту опцию.

`Rotor angle definition` - Контрольная точка для измерения угла ротора
`Angle between the a-phase magnetic axis and the d-axis` (по умолчанию) | `Angle between the a-phase magnetic axis and the q-axis`

Контрольная точка для измерения угла ротора. Значение по умолчанию Angle between the a-phase magnetic axis and the d-axis. Это определение показано на рисунке Конструкции. Когда вы выбираете это значение, потоки ротора и a-фазы выравниваются, когда угол ротора равен нулю.

Другое значение, которое вы можете выбрать Angle between the a-phase magnetic axis and the q-axis. Когда вы выбираете это значение, ток a-фазы генерирует максимальный крутящий момент, когда угол ротора равен нулю.

Механический

`Rotor inertia` - Инерция ротора
`0.01` `kg*m^2` (по умолчанию) | скаляром

Инерция ротора, присоединенного к механическому поступательному порту R. Значение может быть нулем.

`Rotor damping` - Демпфирование ротора
`0` `N*m/(rad/s)` (по умолчанию) | скаляром

Вращательное демпфирование.

Примеры моделей

Шестифазное управление крутящим моментом PMSM

Управляйте крутящим моментом в тяговом приводе на основе шестифазной синхронной машины с постоянными магнитами (PMSM). Источник постоянного напряжения питает PMSM через два управляемых трехфазных преобразователя. PMSM работает как в моторном, так и в генерирующем режимах в соответствии с нагрузкой. Идеальный источник скорости вращения обеспечивает нагрузку. Подсистема управления использует разомкнутый подход для управления крутящим моментом и замкнутый подход для управления током. В каждый момент выборки запрос крутящего момента преобразуется в соответствующую ссылка тока. Текущее управление основано на ПИ. В симуляции используется несколько шагов крутящего момента как в режиме двигателя, так и в режиме генератора. Подсистема Возможностей содержит возможности, которые позволяют вам видеть результаты симуляции.

Шестифазное управление скоростью PMSM

Управляйте скоростью вращения ротора в тяговом электроприводе, основанном на шестифазной синхронной машине с постоянными магнитами (PMSM). Источник постоянного напряжения питает PMSM через два управляемых трехфазных преобразователя. PMSM работает как в моторном, так и в генерирующем режимах в соответствии с нагрузкой. Идеальный источник крутящего момента обеспечивает нагрузку. Подсистема Возможностей содержит возможности, которые позволяют вам видеть результаты симуляции. Подсистема управления включает основанную на ПИ структуру каскадного регулирования, которая имеет внешний цикл угловой скорости и четыре внутренних контура управления током. В течение одной секунды симуляции уставка по скорости вращения составляет 0 об/мин, 500 об/мин, 2000 об/мин и затем 3000 об/мин.

Ссылки

[1] Krause, Paul, Oleg Wasynczuk, Scott Sudhoff, and Steven Pekarek, eds. Анализ электрических машин и приводных систем. Хобокен, Нью-Джерси, США: John Wiley & Sons, Inc., 2013. https://doi.org/10.1002/9781118524336.

[2] Су, Цзянь Ён, Цзинь Бо Ян и Гуи Цзе Ян. Исследования в области управления векторами и методы шестифазного PMSM. Перспективные исследования материалов 516-517 (май 2012): 1626-31. https://doi.org/10.4028/www.scientific.net/AMR.516-517.1626.

Документация

PMSM (Six-Phase)

Описание

Уравнения

Упрощенные электрические уравнения

Переменные

Порты

Сохранение

~ABC - Обмотки ABC статора электрический

~XYZ - Обмотки XYZ статора электрический

n1 - нейтральная точка обмотки ABC электрический

Зависимости

n2 - нейтральная точка обмотки XYZ электрический

Зависимости

R - Ротор мотора механический вращательный

C - Корпус мотора механический вращательный

Параметры

Главный

Number of pole pairs - Количество пар полюсов 6 (по умолчанию) | скаляром

Permanent magnet flux linkage parameterization - Параметризация потокосцепления с постоянными магнитами Specify flux linkage (по умолчанию) | Specify torque constant | Specify back EMF constant

Permanent magnet flux linkage - редактирование с постоянными магнитами 0.03 Wb (по умолчанию) | скаляром

Зависимости

Torque constant - Крутящий момент константа 0.18 N*m/A (по умолчанию) | скаляром

Зависимости

Back EMF constant - Коэффициент противо-ЭДС, постоянная 0.18 V/(rad/s) (по умолчанию) | скаляром

Зависимости

Stator parameterization - Параметризация статора Specify Ld, Lq, and L0 (по умолчанию) | Specify Ls, Lm, and Ms

Stator d-axis inductance, Ld - Индуктивность d статора 0.00019 H (по умолчанию) | скаляром

Зависимости

Stator q-axis inductance, Lq - Индуктивность q статора 0.00025 H (по умолчанию) | скаляром

Зависимости

Stator zero-sequence inductance, L0 - Индуктивность нулевой последовательности статора 0.00016 H (по умолчанию) | скаляром

Зависимости

Stator self-inductance per phase, Ls - Самоиндуктивность статора на фазу 0.0002 H (по умолчанию) | скаляром

Зависимости

Stator inductance fluctuation, Lm - Колебания индуктивности статора -0.00002 H (по умолчанию) | скаляром

Зависимости

Stator mutual inductance, Ms - Взаимная индуктивность статора 0.00002 H (по умолчанию) | скаляром

Зависимости

Stator resistance per phase, Rs - Сопротивление статора на фазу 0.013 Ohm (по умолчанию) | скаляром

Zero sequence - Опция нулевой последовательности Include (по умолчанию) | Exclude

Rotor angle definition - Контрольная точка для измерения угла ротора Angle between the a-phase magnetic axis and the d-axis (по умолчанию) | Angle between the a-phase magnetic axis and the q-axis

Механический

Rotor inertia - Инерция ротора 0.01 kg*m^2 (по умолчанию) | скаляром

Rotor damping - Демпфирование ротора 0 N*m/(rad/s) (по умолчанию) | скаляром

Примеры моделей

Шестифазное управление крутящим моментом PMSM

Шестифазное управление скоростью PMSM

Ссылки

Расширенные возможности

Генерация кода C/C + + Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

См. также

Simscape Electrical документация

Поддержка

`~ABC` - Обмотки ABC статора
электрический

`~XYZ` - Обмотки XYZ статора
электрический

`n1` - нейтральная точка обмотки ABC
электрический

`n2` - нейтральная точка обмотки XYZ
электрический

`R` - Ротор мотора
механический вращательный

`C` - Корпус мотора
механический вращательный

`Number of pole pairs` - Количество пар полюсов
`6` (по умолчанию) | скаляром

`Permanent magnet flux linkage parameterization` - Параметризация потокосцепления с постоянными магнитами
`Specify flux linkage` (по умолчанию) | `Specify torque constant` | `Specify back EMF constant`

`Permanent magnet flux linkage` - редактирование с постоянными магнитами
`0.03` `Wb` (по умолчанию) | скаляром

`Torque constant` - Крутящий момент константа
`0.18` `N*m/A` (по умолчанию) | скаляром

`Back EMF constant` - Коэффициент противо-ЭДС, постоянная
`0.18` `V/(rad/s)` (по умолчанию) | скаляром

`Stator parameterization` - Параметризация статора
`Specify Ld, Lq, and L0` (по умолчанию) | `Specify Ls, Lm, and Ms`

`Stator d-axis inductance, Ld` - Индуктивность d статора
`0.00019` `H` (по умолчанию) | скаляром

`Stator q-axis inductance, Lq` - Индуктивность q статора
`0.00025` `H` (по умолчанию) | скаляром

`Stator zero-sequence inductance, L0` - Индуктивность нулевой последовательности статора
`0.00016` `H` (по умолчанию) | скаляром

`Stator self-inductance per phase, Ls` - Самоиндуктивность статора на фазу
`0.0002` `H` (по умолчанию) | скаляром

`Stator inductance fluctuation, Lm` - Колебания индуктивности статора
`-0.00002` `H` (по умолчанию) | скаляром

`Stator mutual inductance, Ms` - Взаимная индуктивность статора
`0.00002` `H` (по умолчанию) | скаляром

`Stator resistance per phase, Rs` - Сопротивление статора на фазу
`0.013` `Ohm` (по умолчанию) | скаляром

`Zero sequence` - Опция нулевой последовательности
`Include` (по умолчанию) | `Exclude`

`Rotor angle definition` - Контрольная точка для измерения угла ротора
`Angle between the a-phase magnetic axis and the d-axis` (по умолчанию) | `Angle between the a-phase magnetic axis and the q-axis`

`Rotor inertia` - Инерция ротора
`0.01` `kg*m^2` (по умолчанию) | скаляром

`Rotor damping` - Демпфирование ротора
`0` `N*m/(rad/s)` (по умолчанию) | скаляром

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®