RST Controller

Прогнозирующее управление с использованием полиномиального представления

Библиотека:
Simscape/Электрический/Управление/Общее управление

Описание

Блок RST Controller реализует обобщенный прогнозирующий контроллер, используя опорный сигнал отслеживающее полиномиальное представление. Схема показывает эквивалентную схему для алгоритма управления.

Уравнения

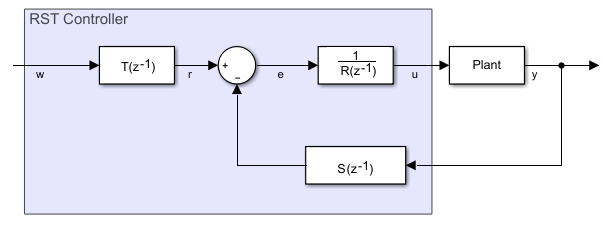
Управляемая авторегрессионная интегрированная модель скользящего среднего значения (CARIMA) описывает объект:

$A (z^{- 1}) y (k) = z^{- d} B (z^{- 1}) u (k - 1) + \frac{e (k) C (z^{- 1})}{D (z^{- 1})}$

$A (z^{- 1}) = 1 + a_{1} z^{- 1} + \dots + a_{n_{A}} z^{- n_{A}}$

$B (z^{- 1}) = b_{0} + b_{1} z^{- 1} + \dots + b_{n_{B}} z^{- n_{B}}$

$C (z^{- 1}) = 1$

$D (z^{- 1}) = 1 - z^{- 1},$

где:

d является системой с потерей времени.
y(k) - выход объекта управления.
u(k) - контроллер выход.
e(k) - белый шум с нулевым средним значением.
A (z^-1) и B (z^-1) являются полиномами системы.
_nA и _nB являются полиномами степеней.
C (z^-1) и D (z^-1) являются полиномами нарушения порядка для получения установившейся ошибки.

Модель предсказания задается как

$\hat{y} (k + j | k) = G_{j - d} (z^{- 1}) D (z^{- 1}) z^{- d - 1} u (k + j) + \frac{H_{j - d} (z^{- 1}) D (z^{- 1})}{C (z^{- 1})} u (k - 1) + \frac{F_{j - d} (z^{- 1})}{C (z^{- 1})} y (k)$

$j = \bar{h i, h p}$

где:

hi - это минимальное предсказание.
hp - горизонт предсказания.

Будущая последовательность управления, вычисленная в момент k,

$u (k + j - 1 | k),$

где

$j = \bar{1, h c}$

а hc - горизонт управления.

Предсказанные значения выхода

$\hat{y} (k + j | k) .$

Чтобы определить полиномы системы, $F_{j - d} (z^{- 1})$ , $G_{j - d} (z^{- 1})$ , и $H_{j - d} (z^{- 1})$ , блок использует два диофантовых уравнения. Первое диофантово уравнение

$\frac{C (z^{- 1})}{A (z^{- 1}) D (z^{- 1})} = E_{j - d} (z^{- 1}) + z^{- j + d} \frac{F_{j - d} (z^{- 1})}{A (z^{- 1}) D (z^{- 1})},$

где:

$E_{j - d} (z^{- 1}) = 1 + 1 + e_{1} z^{- 1} + \dots + e_{n_{E}} z^{- n_{E}}$

$F_{j - d} (z^{- 1}) = f_{0} + f_{1} z^{- 1} + \dots + f_{n_{F}} z^{- n_{F}}$

$n_{E} = j - d - 1$

$n_{F} = max (n_{A} + n_{D} - 1, n_{C} - j + d)$

Второе диофантово уравнение

$E_{j - d} (z^{- 1}) B (z^{- 1}) = C (z^{- 1}) G_{j - d} (z^{- 1}) + z^{- j + d} H_{j - d} (z^{- 1}),$

где:

$G_{j - d} (z^{- 1}) = g_{0} + g_{1} z^{- 1} + \dots + g_{n_{G}} z^{- n_{G}}$

$H_{j - d} (z^{- 1}) = h_{0} + h_{1} z^{- 1} + \dots + h_{n_{H}} z^{- n_{H}}$

$n_{G} = j - d - 1$

$n_{H} = max (n_{C}, n_{B} + d) - 1$

Получившаяся модель предсказания

$\hat{y} (k + j | k) = G_{j - d} (z^{- 1}) D (z^{- 1}) z^{- d - 1} u (k + j) + {\hat{y}}_{0} (k + j | k),$

где

${\hat{y}}_{0} (k + j | k) = \frac{H_{j - d} (z^{- 1}) D (z^{- 1})}{C (z^{- 1})} u (k - 1) + \frac{F_{j - d} (z^{- 1})}{C (z^{- 1})} y (k)$

представляет свободный ответ системы.

Используя матричное обозначение, модель предсказания может быть записана как

$\hat{y} = {Gu}_{d} + {\hat{y}}_{0},$

где:

$\hat{y} = {[\hat{y} (k + h i | k), \hat{y} (k + h i + 1 | k), \dots, \hat{y} (k + h p | k)]}^{T}$

$G = [\begin{matrix} g_{h i - d - 1} & \dots & g_{0} & 0 & \dots & 0 \\ g_{h i - d} & \dots & g_{1} & g_{0} & \dots & 0 \\ \dots & \dots & \dots & \dots & \dots & \dots \\ g_{h c - 1} & \dots & \dots & \dots & \dots & g_{0} \\ g_{h p - d - 1} & \dots & \dots & \dots & \dots & g_{h p - h c - 1} \end{matrix}]$

$u_{d} = {[D (z^{- 1}) u (k), \dots, D (z^{- 1}) u (k + h c - 1)]}^{T}$

${\hat{y}}_{0} = {[{\hat{y}}_{0} (k + h i | k), {\hat{y}}_{0} (k + h i + 1 | k), \dots, {\hat{y}}_{0} (k + h p | k)]}^{T}$

Чтобы минимизировать ошибку отслеживания и контроллер выход, блок использует функцию затрат. Чтобы компромиссировать между минимизацией ошибки отслеживания и минимизацией контроллер выхода, блок использует весовой коэффициент

$J = {({Gu}_{d} + {\hat{y}}_{0} - w)}^{T} ({Gu}_{d} + {\hat{y}}_{0} - w) + λ u_{d}^{T} u_{d}$

для

$D (z^{- 1}) u (k + i) = 0$

$i \in [h c, h p - d - 1],$

где w - ссылка траектории. Минимизация функции стоимости приводит к уравнению для оптимальной последовательности управления:

$u_{d}^{*} = (G^{T} G + λ Я_{h c}) G^{T} [w - {\hat{y}}_{0}] .$

Как _γj и $j = \bar{h i, h p}$ являются элементами в первой строке матрицы ${(G^{T} G + λ Я_{h c})}^{- 1} G^{T}$ , применение принципа отступающего горизонта приводит к уравнению алгоритма управления как

$D (z^{- 1}) u (k) = \sum_{j = h i}^{h p} γ_{j} [w (k + j | k) - {\hat{y}}_{0} (k + j | k)] .$

Замена с использованием ${\hat{y}}_{0} (k + j | k) = \frac{H_{j - d} (z^{- 1}) D (z^{- 1})}{C (z^{- 1})} u (k - 1) + \frac{F_{j - d} (z^{- 1})}{C (z^{- 1})} y (k)$ приводит к такой форме уравнения алгоритма управления:

$C (z^{- 1}) D (z^{- 1}) u (k) = - \sum_{j = h i}^{h p} γ_{j} H_{j - d} (z^{- 1}) D (z^{- 1}) u (k - 1) - \sum_{j = h i}^{h p} γ_{j} F_{j - d} (z^{- 1}) y (k) + \sum_{j = h i}^{h p} γ_{j} C (z^{- 1}) w (k + j) .$

Полиномиальная форма алгоритма управления следующая как

$R (z^{- 1}) u (k) + S (z^{- 1}) y (k) = T (z^{- 1}) w (k + h p),$

где:

$R (z^{- 1}) = (C (z^{- 1}) + \sum_{j = h i}^{h p} γ_{j} z^{- 1} H_{j - d} (z^{- 1})) D (z^{- 1}),$

$S (z^{- 1}) = \sum_{j = h i}^{h p} γ_{j} F_{j - d} (z^{- 1}),$

$T (z^{- 1}) = C (z^{- 1}) \sum_{j = h i}^{h p} γ_{j} z^{- h p + j} .$

Ограничения

Чтобы получить R, R и T полиномы, используйте дискретное время вместо передаточной функции в непрерывном времени.

Порты

Вход

расширить все

`r` - Ссылка на объект
скаляр

Опорный сигнал системы объекта.

Типы данных: single | double

`y` - Производительность объекта
скаляр

Выходной сигнал системы объекта.

Типы данных: single | double

Выход

расширить все

`u` - Контроллер выход
скаляр

Выходной сигнал системы управления.

Типы данных: single | double

Параметры

расширить все

`Controller parameterization` - Метод параметризации
`Controller polynomials` (по умолчанию) | `Generate polynomials`

Метод параметризации контроллера. Если вы знаете R, S и T полиномиальные значения в дискретном времени, выберите Controller polynomials. В противном случае выберите Generate polynomials.

Зависимости

Выбор метода параметризации включает другие параметры.

`R polynomial` - R полиномиальные значения
`1` (по умолчанию) | положительный, скалярный или вектор

Вектор R полиномов для управления RST.

Зависимости

Выбор Controller polynomials для параметра Controller parameterization включает этот параметр.

`S polynomial` - S полиномиальные значения
`1` (по умолчанию) | положительный, скалярный или вектор

Вектор S полиномов для управления RST.

Зависимости

Выбор Controller polynomials для параметра Controller parameterization включает этот параметр.

`T polynomial` - T полиномиальные значения
`1` (по умолчанию) | положительный, скалярный или вектор

Вектор T полиномов для управления RST.

Зависимости

Выбор Controller polynomials для параметра Controller parameterization включает этот параметр.

`Model discrete transfer function numerator` - Передаточный числитель функций
`1` (по умолчанию) | скаляром или вектором

Числитель дискретизированной передаточной функции системы. Чтобы определить дискретную передаточную функцию, если у вас есть лицензия для Control System Toolbox™, используйте c2d функция.