hinfgs

Синтез контроллеров H ∞ по расписанию усиления

Синтаксис

[gopt,pdK,R,S] = hinfgs(pdP,r,gmin,tol,tolred)

Описание

Учитывая аффинное зависящее от параметра объект

$P {\begin{matrix} \dot{x} = A (p) x + B_{1} (p) w + B_{2} u \\ z = C_{1} (p) x + D_{11} (p) w + D_{12} u \\ y = C_{2} x + D_{21} w + D_{22} u \end{matrix}$

где изменяющийся во времени вектор параметра p (t) колеблется в кубе и измеряется в реальном времени, hinfgs ищет аффинный зависящий от параметра контроллер

$K {\begin{matrix} \dot{ζ} = A_{K} (p) ζ + B_{K} (p) y \\ u = C_{K} (p) ζ + D_{K} (P) y \end{matrix}$

запланированный по измерениям p (t) и таким, что

K стабилизирует систему с обратной связью
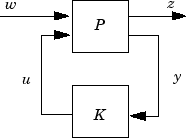
для всех допустимых траекторий параметров p (t)
K минимизирует квадратичную H с обратной связью ∞ эффективность от w до z.

Описание pdP зависящего от параметра объекта P задается как psys и вектор r задает количество входов и выходов контроллера (set r=[p2,m2] если y ∊ R^p² и u ∊ R^m²). Обратите внимание, что hinfgs также принимает политопическую модель возвращаемых P, например, aff2pol.

hinfgs возвращает оптимальную квадратичную эффективность с обратной связью gopt и политопическое описание контроллера, запланированного по усилению pdK. Чтобы проверить, достижима ли квадратичная γ эффективности с обратной связью, установите третий вход gmin к γ. Аргументы tol и tolred управляйте необходимой относительной точностью на gopt и порог для сокращения порядка. Наконец, hinfgs также возвращает решения R, S характеристической системы LMI.

Реализация контроллера

Контроллер, запланированный по усилению pdK параметризируется p (t) и характеризуется значениями _KΠj $(\begin{matrix} A_{K} (p) & B_{K} (p) \\ C_{K} (p) & D_{K} (p) \end{matrix})$ в углах ³ j поля параметра. Команда

Kj = psinfo(pdK,'sys',j)

возвращает j -й вершинный контроллер _K Πj в то время как

pv = psinfo(pdP,'par') 
vertx = polydec(pv) 
Pj = vertx(:,j)

задает соответствующий угол ³ j поля параметра (pv - описание вектора параметра).

Планирование контроллера должно выполняться следующим образом. Учитывая p (t) измерений параметров в t времени,

Экспресс- p (t) как выпуклая комбинация _³ j:
$p (t) = α_{1} {^{3}}_{1} + \dots + α_{N} {^{3}}_{N}, α_{j} \geq 0, \sum_{i = 1}^{N} α_{j} = 1$
Это выпуклое разложение вычисляется polydec.
Вычислите матрицы пространства состояний контроллера в то время t как выпуклая комбинация вершинных контроллеров _KΠj:
$(\begin{matrix} A_{K} (t) & B_{K} (t) \\ C_{K} (t) & D_{K} (t) \end{matrix}) = \sum_{i = 1}^{N} α_{j} K_{Π}_{_{ι}} .$
Используйте _AK (<reservedrangesplaceholder6>), B <reservedrangesplaceholder5> (<reservedrangesplaceholder4>), C <reservedrangesplaceholder3> (<reservedrangesplaceholder2>), D <reservedrangesplaceholder1> (<reservedrangesplaceholder0>), чтобы обновить уравнения пространства состояний контроллера.

Ссылки

Apkarian, P., P. Gahinet, and G. Becker, «Self-Scheduled H ∞ Control of Linear Parameter-Variing Systems», Automatica, 31 (1995), pp. 1251-1261.

Becker, G., Packard, P., «Робастная Эффективности линейно-параметрически изменяющихся систем с использованием параметрически-зависимой линейной обратной связи», Systems and Control Букв, 23 (1994), pp. 205-215.

Packard, A. «, Табличное управление через линейные дробные преобразования», System. Contr. Буквы, 22 (1994), стр. 79-92.

См. также

pdsimul | polydec | psys | pvec

Представлено до R2006a

Документация