Функция чувствительности и дополнительная функция чувствительности являются двумя передаточными функциями, связанными с робастностью и эффективностью системы с обратной связью. Рассмотрим общую многомерную структуру управления с обратной связью, как на следующем рисунке.
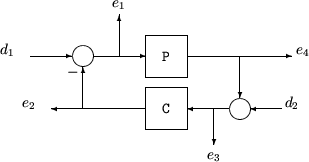
В следующей таблице приведены значения входных и выходных функций чувствительности для этой структуры управления.
Описание | Уравнение |
|---|---|
Входная Si чувствительности (передаточная функция с обратной связью от d 1 до e 1) | Si = (I + CP)–1 |
Входная дополнительная Ti чувствительности (передаточная функция с обратной связью от d 1 до e 2) | Ti = CP (I + CP)–1 |
Выходная So чувствительности (передаточная функция с обратной связью от d 2 до e 2) | So = (I + PC)–1 |
Выходная дополнительная To чувствительности (передаточная функция с обратной связью от d 2 до e 4) | To = PC (I + PC)–1 |
Передаточная функция входного цикла Li | Li = CP |
Передаточная функция выходного цикла Lo | Lo = PC |
Когда у вас есть неопределенная модель объекта управления и модели контроллеров, можно вычислить функции чувствительности и дополнительной чувствительности в худшем случае для анализа робастности. Для этого создайте передаточную функцию, которую необходимо вычислить и использовать wcgain найти возмущения, которые приводят к худшему усилению для этой передаточной функции. Затем используйте usubs вычислить передаточную функцию, соответствующую этому усилению в худшем случае.
В данном примере создайте SISO неопределенный объект P и ПИД-регулятора.
delta = ultidyn('delta',[1 1]); tau = ureal('tau',5,'range',[4 6]); P = tf(1,[tau 1])*(1+0.25*delta); C = pid(4,4);
Создайте неопределенную чувствительность и дополнительные передаточные функции чувствительности, и , соответственно. (Для этой системы SISO входная и выходная функции чувствительности равны.)
Si = feedback(1,C*P); Ti = 1 - Si;
Вычислите наихудшие пиковые усиления Si и Ti и соответствующие наихудшие возмущения с использованием wcgain.
[wcgS,wcuS] = wcgain(Si); [wcgT,wcuT] = wcgain(Ti);
Наконец, оцените функции чувствительности с этими худшими нарушениями.
Siwc = usubs(Si,wcuS); Tiwc = usubs(Ti,wcuT);
Siwc и Tiwc являются функциями чувствительности и дополнительной чувствительности в худшем случае для неопределенности, указанной на объекте. Исследуйте эффект неопределенности на функцию чувствительности Si путем построения графика частотной характеристики некоторых выборок. Фактический пик усиления в худшем случае wcgS может быть значительно выше, чем показывают случайные выборки.
rng(0); % for reproducibility
sigma(Si,Siwc)