В проекте устойчивого управления эффективность выражается и измеряется в терминах пикового усиления (H ∞ норма или пиковое сингулярное значение) системы. Чем меньше этот коэффициент усиления, тем выше производительность системы. Эффективность номинально стабильной неопределенной системы, как правило, ухудшается при увеличениях степени неопределенности. Используйте анализ робастности и анализ наихудшего случая, чтобы изучить, как количество неопределенности в вашей системе влияет на стабильность и пиковый коэффициент усиления системы.
Анализ робастности посвящен нахождению максимального количества неопределенности, совместимого со стабильностью или с заданным уровнем эффективности. Следующий рисунок показывает типовую кривую компромисса между эффективностью и робастностью. Здесь пиковое усиление (пиковая величина на диаграмме Боде или сингулярном графике) характеризует производительность системы.
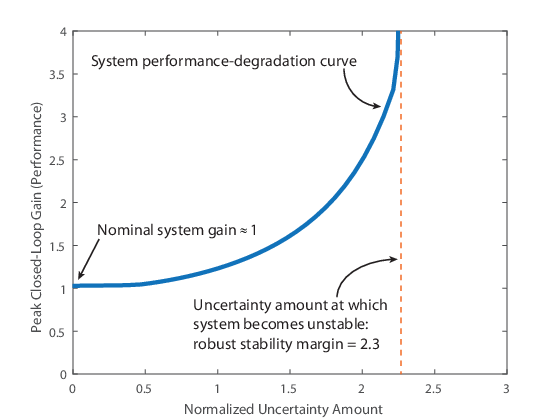
Ось x количественно определяет нормированное количество неопределенности. Значение x = 1 соответствует областям значений неопределенности, заданным в модели. x = 2 представляет систему с вдвое большей неопределенностью. x = 0 соответствует номинальной системе. ( См.actual2normalized для получения дополнительной информации о нормализованных областях значений неопределенности.) Ось y является эффективностью, измеренной как пиковое усиление некоторой передаточной функции с обратной связью. Для образца, если передаточная функция с обратной связью измеряет чувствительность сигнала ошибки к некоторому нарушению порядка, то более высокий коэффициент усиления пика соответствует более плохому подавлению помех.
Когда все неопределенные элементы установлены в свои номинальные значения (x = 0), коэффициент усиления системы является его номинальным значением. На рисунке номинальный коэффициент усиления системы составляет около 1. Когда область значений значений, которые могут принимать неопределенные элементы, увеличивается, пиковый коэффициент усиления в области значений неопределенностей увеличивается. Тяжелая синяя линия представляет пиковое усиление и называется system performance degradation curve. Он увеличивается монотонно как функция от величины неопределенности.
Кривая ухудшения производительности системы обычно имеет вертикальную асимптоту, соответствующую robust stability margin. Этот запас является максимальной степенью неопределенности, которую система может терпеть, оставаясь стабильной. Для системы предыдущего рисунка пиковое усиление становится бесконечным около x = 2,3. Другими словами, система становится нестабильной, когда область значений неопределенности в 2,3 раза превышает заданный в модели (в нормализованных модулях). Поэтому устойчивый запас устойчивости составляет 2,3. Чтобы вычислить устойчивый запас устойчивости для неопределенной системной модели, используйте robstab функция.
robust performance margin для данного усиления, γ, является максимальной величиной неопределенности, которую система может терпеть, имея пиковый коэффициент усиления меньше γ. Для примера на следующем рисунке предположим, что вы хотите сохранить пик усиления в замкнутом цикле ниже 1,8. Для этого пикового усиления устойчивый запас эффективности составляет около 1,7. Это значение означает, что пиковый коэффициент усиления системы остается ниже 1,8, пока неопределенность остается в пределах 1,7 раза выше заданной неопределенности (в нормализованных модулях).
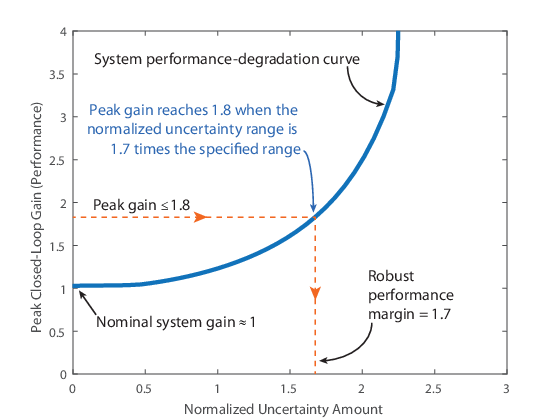
Чтобы вычислить устойчивый запас по эффективности для неопределенной системной модели, используйте robgain функция.
Это worst-case gain является самым большим значением, которое пиковое усиление может взять на себя определенную область значений неопределенности. Это значение является аналогом надежного запаса по эффективности. В то время как устойчивый запас эффективности измеряет максимальное количество неопределенности, совместимое с конкретным пиковым уровнем усиления, в худшем случае коэффициент усиления измеряет максимальное усиление, связанное с конкретной величиной неопределенности. Для образца на следующем рисунке наихудший коэффициент усиления для величины неопределенности, указанной в модели, составляет около 1,20. Если эта сумма неопределенности удвоена, усиление в худшем случае увеличивается до 2,5.
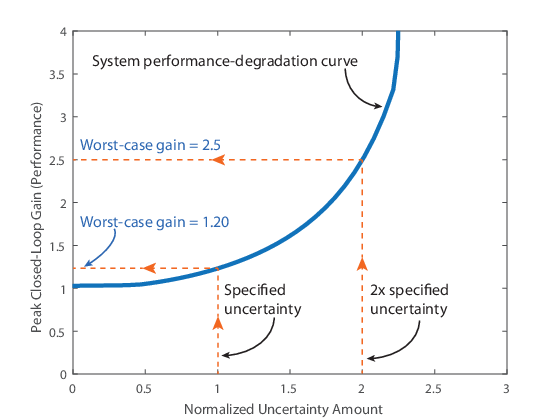
Чтобы вычислить коэффициент усиления в худшем случае для неопределенной системной модели, используйте wcgain функция. The ULevel опция wcOptions команда позволяет вам вычислить коэффициент усиления в худшем случае для различных величин неопределенности.