Как алгоритм оптимизации формулирует задачи минимизации

Когда вы оптимизируете параметры Simulink^® Модель для удовлетворения проекта требований программное обеспечение Simulink Design Optimization™ автоматически преобразует требования в ограниченную задачу оптимизации, а затем решает проблему с помощью методов оптимизации. Ограниченная задача оптимизации итеративно моделирует модель Simulink, сравнивает результаты симуляций с целями ограничений и использует методы оптимизации, чтобы настроить настроенные параметры, чтобы лучше соответствовать целям.

В этом разделе описывается, как программное обеспечение формулирует ограниченную задачу оптимизации, используемую алгоритмами оптимизации. Для каждого алгоритма оптимизации программное обеспечение формулирует один из следующих типов задач минимизации:

Выполнимость
Отслеживание
Смешанная осуществимость и отслеживание

Для получения дополнительной информации о том, как каждый алгоритм оптимизации формулирует эти проблемы, смотрите:

Задача выполнимости и формулировка ограничений

Feasibility означает, что алгоритм оптимизации находит значения параметров, которые удовлетворяют всем ограничениям в пределах заданных допусков, но не минимизирует при этом какую-либо цель или функцию затрат.

На следующем рисунке x 1, _x 3 и xn представляют комбинацию значений параметров P 1 и P 2 и являются допустимыми решениями, потому что они не нарушают ограничение нижней границы.

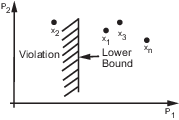
В модели Simulink вы ограничиваете сигнал, задавая нижнюю и верхнюю границы в блоке Check (Check Step Response Characteristics,...) или объекте требования (sdo.requirements.StepResponseEnvelope,...), как показано на следующем рисунке.

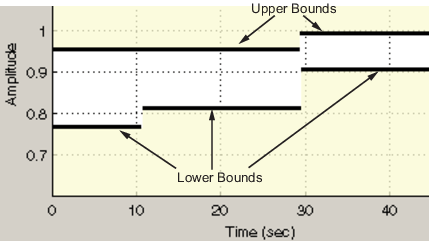
Эти ограничения piecewise linear bounds. Кусочно-линейная связанная _ybnd с n ребрами может быть представлена как:

$y_{b n d} (t) = {\begin{matrix} y_{1} (t) & t_{1} \leq t \leq t_{2} \\ y_{2} (t) & t_{2} \leq t \leq t_{3} \\ ⋮ & ⋮ \\ y_{n} (t) & t_{n} \leq t \leq t_{n + 1} \end{matrix},$

Программа вычисляет расстояние со знаком между симулированным откликом и ребром. Расстояние со знаком для нижних границ:

$\begin{array}{l} c = [\begin{array}{l} \max_{t_{1} \leq t \leq t_{2}} y_{b n d} - y_{s i m} \\ \max_{t_{2} \leq t \leq t_{3}} y_{b n d} - y_{s i m} \\ \max_{t_{n} \leq t \leq t_{n + 1}} y_{b n d} - y_{s i m} \end{array}], \end{array}$

где _ysim является симулированным откликом и является функцией оптимизируемых параметров.

Расстояние со знаком для верхних границ:

$c = [\begin{matrix} \max_{t_{1} \leq t \leq t_{2}} y_{s i m} - y_{b n d} \\ \max_{t_{2} \leq t \leq t_{3}} y_{s i m} - y_{b n d} \\ \max_{t_{n} \leq t \leq t_{n + 1}} y_{s i m} - y_{b n d} \end{matrix}] .$

В командной строке optimFcn поставляет c непосредственно от Cleq область vals.

Если все ограничения удовлетворены (c ≤ 0) для некоторой комбинации значений параметров, то это решение, как говорят, является допустимым. На следующем рисунке x 1 и _x 3 являются допустимыми решениями.

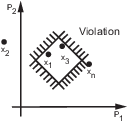
Когда ваша модель имеет несколько требований или векторных сигналов, питающих требование, вектор ограничений расширяется с нарушениями ограничений для каждого сигнала и связан:

$C = [c_{1}; c_{2}; \dots; c_{n}] .$

Задача отслеживания

В сложение к нижней и верхней границам можно задать опорный сигнал в блоке Check Against Reference или sdo.requirements.SignalTracking объект, который может отслеживать выходы модели Simulink. Цель отслеживания является целью отслеживания суммарной квадратной ошибки.

Вы задаете опорный сигнал как последовательность пар временной амплитуды:

$y_{r e f} (t_{r e f}), t_{r e f} \in {T_{r e f 0}, T_{r e f 1}, \dots, T_{r e f N}} .$

Программа вычисляет симулированный отклик как последовательность пар временной амплитуды:

$y_{s i m} (t_{s i m}), t_{s i m} \in {T_{s i m 0}, T_{s i m 1}, \dots, T_{s i m N}},$

где некоторые значения _tsim могут совпадать со значениями _tref.

Новая временная основа, _tnew, формируется из объединения элементов _tref и _tsim. Элементы, которые не находятся в пределах минимально-максимальной области значений как _tref, так и _tsim, опущены:

$t_{n e w} = {t : t_{s i m} \cup t_{r e f}}$

Используя линейную интерполяцию, программа вычисляет значения _yref и _ysim в то время, точки в _tnew, а затем вычисляет масштабированную ошибку:

$e (t_{n e w}) = \frac{(y_{s i m} (t_{n e w}) - y_{r e f} (t_{n e w}))}{\max_{t_{n e w}} | y_{r e f} |} .$

Наконец, программа вычисляет взвешенную, интегральную квадратную ошибку:

$f = \int w (t) e {(t)}^{2} d t .$

Примечание

По умолчанию w веса (t) равен 1. Задавать разное значение веса можно только в командной строке.

Когда ваша модель имеет требования или векторные сигналы, подающие требование, цель отслеживания равняется сумме отдельных интегральных ошибок отслеживания для каждого сигнала:

$F = \sum f_{i} .$

Формулировки задачи метода градиентного спуска

Метод Градиентного спуска использует функцию fmincon оптимизировать параметры модели для удовлетворения проектных требований.

Тип задачи	Формулировка задачи
Задача выполнимости	Программа формулирует C ограничений (x), как описано в «Задача выполнимости» и «Формулировка ограничений». Если вы выбираете максимально возможное решение опции (т.е. оптимизация продолжается после нахождения начального возможного решения), программное обеспечение использует следующую формулировку задачи: $\begin{array}{l} \min_{[x, γ]} γ \\ s . t . C (x) \leq γ \\ \underline{x} \leq x \leq \bar{x} \\ γ \leq 0 \end{array}$ y является переменной slack, которая допускает возможное решение с C (x) ≤ β, а не C (x) ≤ 0. Если вы не выбираете максимально возможное решение опции (т.е. оптимизация прекращается, как только возможное решение найдено), программное обеспечение использует следующую формулировку задачи: $\begin{array}{l} \min_{x} 0 \\ s . t . C (x) \leq 0 \\ \underline{x} \leq x \leq \bar{x} \end{array}$
Задача отслеживания	Программное обеспечение формулирует F (x) цели слежения, как описано в Задаче слежения и минимизирует цель слежения: $\begin{array}{l} \min_{x} F (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$
Смешанная задача выполнимости и отслеживания	Программное обеспечение минимизирует следующую формулировку задачи: $\begin{array}{l} \min_{x} F (x) \\ s . t . C (x) \leq 0 \\ \underline{x} \leq x \leq \bar{x} \end{array}$ Примечание При отслеживании опорного сигнала программное обеспечение игнорирует максимально возможное решение опции.

Тип задачи

Формулировка задачи

Задача выполнимости

Программа формулирует C ограничений (x), как описано в «Задача выполнимости» и «Формулировка ограничений».

Если вы выбираете максимально возможное решение опции (т.е. оптимизация продолжается после нахождения начального возможного решения), программное обеспечение использует следующую формулировку задачи:
$\begin{array}{l} \min_{[x, γ]} γ \\ s . t . C (x) \leq γ \\ \underline{x} \leq x \leq \bar{x} \\ γ \leq 0 \end{array}$
y является переменной slack, которая допускает возможное решение с C (x) ≤ β, а не C (x) ≤ 0.
Если вы не выбираете максимально возможное решение опции (т.е. оптимизация прекращается, как только возможное решение найдено), программное обеспечение использует следующую формулировку задачи:
$\begin{array}{l} \min_{x} 0 \\ s . t . C (x) \leq 0 \\ \underline{x} \leq x \leq \bar{x} \end{array}$

Задача отслеживания

Программное обеспечение формулирует F (x) цели слежения, как описано в Задаче слежения и минимизирует цель слежения:

$\begin{array}{l} \min_{x} F (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$

Смешанная задача выполнимости и отслеживания

Программное обеспечение минимизирует следующую формулировку задачи:

$\begin{array}{l} \min_{x} F (x) \\ s . t . C (x) \leq 0 \\ \underline{x} \leq x \leq \bar{x} \end{array}$

Примечание

При отслеживании опорного сигнала программное обеспечение игнорирует максимально возможное решение опции.

Simplex Search Метод Формулировок задачи

Метод Simplex Search использует функцию fminsearch и fminbnd оптимизировать параметры модели для удовлетворения проектных требований. fminbnd используется, если оптимизируется один скалярный параметр, в противном случае fminsearch используется. Вы не можете использовать ограничения параметров $\underline{x} \leq x \leq \bar{x}$ с fminsearch.

Тип задачи	Формулировка задачи
Задача выполнимости	Программа формулирует C ограничений (x), как описано в «Задача выполнимости и формулировка ограничений», а затем минимизирует максимальное нарушение ограничений: $\min_{x} макс. (C (x))$
Задача отслеживания	Программное обеспечение формулирует F (x) цели слежения, как описано в Задаче слежения, а затем минимизирует цель слежения: $\min_{x} F (x)$
Смешанная задача выполнимости и отслеживания	Программа формулирует задачу в два этапа: Находит возможное решение. $\min_{x} макс. (C (x))$ Минимизирует цель отслеживания. Программное обеспечение использует результаты шага 1 в качестве начальных догадок и поддерживает выполнимость путем введения прерывистого барьера в цель оптимизации. $\begin{array}{l} \min_{x} Γ (x) \\ где \\ Γ (x) = {\begin{array}{l} \infty & если \max (C (x)) > 0 \\ F (x) & иначе . \end{array} \end{array}$

Тип задачи

Формулировка задачи

Задача выполнимости

Программа формулирует C ограничений (x), как описано в «Задача выполнимости и формулировка ограничений», а затем минимизирует максимальное нарушение ограничений:

$\min_{x} макс. (C (x))$

Задача отслеживания

Программное обеспечение формулирует F (x) цели слежения, как описано в Задаче слежения, а затем минимизирует цель слежения:

$\min_{x} F (x)$

Смешанная задача выполнимости и отслеживания

Программа формулирует задачу в два этапа:

Находит возможное решение.
$\min_{x} макс. (C (x))$
Минимизирует цель отслеживания. Программное обеспечение использует результаты шага 1 в качестве начальных догадок и поддерживает выполнимость путем введения прерывистого барьера в цель оптимизации.
$\begin{array}{l} \min_{x} Γ (x) \\ где \\ Γ (x) = {\begin{array}{l} \infty & если \max (C (x)) > 0 \\ F (x) & иначе . \end{array} \end{array}$

Метод Поиска Шаблона Формулировки задачи

Метод Pattern Search использует функцию patternsearch (Global Optimization Toolbox) для оптимизации параметров модели в соответствии с требованиями проекта.

Тип задачи	Формулировка задачи
Задача выполнимости	Программа формулирует C ограничений (x), как описано в «Задача выполнимости и формулировка ограничений», а затем минимизирует максимальное нарушение ограничений: $\begin{array}{l} \min_{x} макс. (C (x)) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$
Задача отслеживания	Программное обеспечение формулирует F (x) цели слежения, как описано в Задаче слежения, а затем минимизирует цель слежения: $\begin{array}{l} \min_{x} F (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$
Смешанная задача выполнимости и отслеживания	Программа формулирует задачу в два этапа: Находит возможное решение. $\begin{array}{l} \min_{x} макс. (C (x)) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$ Минимизирует цель отслеживания. Программное обеспечение использует результаты шага 1 в качестве начальных догадок и поддерживает выполнимость путем введения прерывистого барьера в цель оптимизации. $\begin{array}{l} \min_{x} Γ (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \\ где \\ Γ (x) = {\begin{array}{l} \infty & если \max (C (x)) > 0 \\ F (x) & иначе . \end{array} \end{array}$

Тип задачи

Формулировка задачи

Задача выполнимости

$\begin{array}{l} \min_{x} макс. (C (x)) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$

Задача отслеживания

$\begin{array}{l} \min_{x} F (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$

Смешанная задача выполнимости и отслеживания

Программа формулирует задачу в два этапа:

Находит возможное решение.
$\begin{array}{l} \min_{x} макс. (C (x)) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$
Минимизирует цель отслеживания. Программное обеспечение использует результаты шага 1 в качестве начальных догадок и поддерживает выполнимость путем введения прерывистого барьера в цель оптимизации.
$\begin{array}{l} \min_{x} Γ (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \\ где \\ Γ (x) = {\begin{array}{l} \infty & если \max (C (x)) > 0 \\ F (x) & иначе . \end{array} \end{array}$

Градиентные расчеты

Для Gradient descent (fmincon) решатель оптимизации, градиенты вычисляются с помощью численного возмущения:

$\begin{array}{l} d x = \sqrt[3]{e p s} \times \max (| x |, \frac{1}{10} x_{t y p i c a l}) \\ d L = \max (x - d x, x_{\min}) \\ d R = \min (x + d x, x_{\max}) \\ F_{L} = o p t_f c n (d L) \\ F_{R} = o p t_f c n (d R) \\ \frac{d F}{d x} = \frac{(F_{L} - F_{R})}{(d L - d R)} \end{array}$

x является скалярной конструктивной переменной.
_xmin - нижняя граница x.
_xmax - верхняя граница x.
_xtypical - масштабированное значение x.
opt_fcn является целевой функцией.

dx относительно велик, чтобы учитывать допустимые отклонения решателя симуляции.

Если вы хотите вычислить градиенты любым другим способом, вы можете сделать это в функции затрат, которую вы записываете для программного выполнения оптимизации проекта. Посмотрите sdo.optimize и GradFcn от sdo.OptimizeOptions для получения дополнительной информации.

Документация