Документация

Загрузите выборочные данные.

Загрузите образец данных панели.

load panelData

Массив набора данных, panelData, содержит ежегодные наблюдения по восьми городам в течение 6 лет. Это моделируемые данные.

Задайте переменные.

Первая переменная, Growth, измеряет экономический рост (переменная отклика). Вторая и третья переменные - индикаторы города и года, соответственно. Последняя переменная, Employ, измеряет занятость (переменная предиктора).

y = panelData.Growth;
city = panelData.City;
year = panelData.Year;
x = panelData.Employ;

Постройте графики данных, сгруппированных по категориям.

Чтобы искать потенциальные фиксированные эффекты конкретного города, создайте прямоугольный график отклика, сгруппированного по городу.

figure()
boxplot(y,city)
xlabel('City')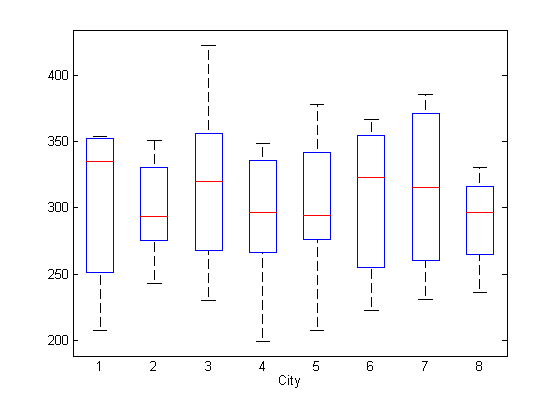

По-видимому, нет никаких систематических различий в среднем ответе между городами.

Отобразите данные, сгруппированные по другой категории.

Чтобы искать потенциальные фиксированные эффекты для конкретного года, создайте прямоугольный график отклика, сгруппированного по годам.

figure()
boxplot(y,year)
xlabel('Year')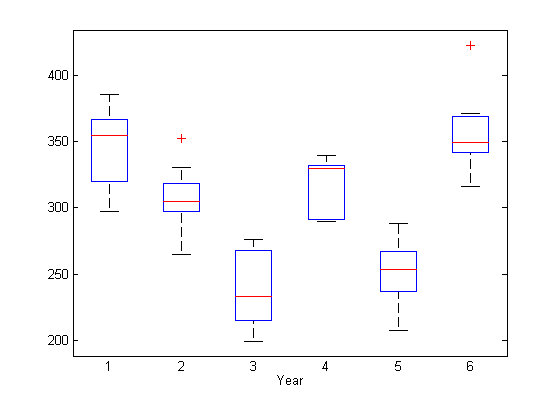

Некоторые доказательства систематических различий в среднем ответе между годами, по-видимому, существуют.

Форматируйте данные отклика.

Позвольте _yij обозначить ответ для city j = 1,..., d, в году i = 1,..., n. Точно так _xij соответствующее значение переменной предиктора. В этом примере n = 6 и d = 8.

Рассмотрите подбор кривой модели фиксированных эффектов для конкретного года с постоянным наклоном и параллельной корреляцией среди городов в том же году,

где $${\epsilon }_i=({\epsilon }_{i1},\dots ,{\epsilon }_{id}{)}^{\prime }\sim MVN(0,\Sigma )$$. Параллельная корреляция учитывает любые неизмеренные, временно-статические факторы, которые могут повлиять на рост аналогично для некоторых городов. Например, города с близкой пространственной близостью могут с большей вероятностью иметь аналогичный экономический рост.

Чтобы подогнать эту модель используя mvregress, измените форму данных отклика на n -by d матрицу.

n = 6; d = 8;
Y = reshape(y,n,d);

Форматы проекта.

Создайте массив ячеек n длины из матриц d -by K design. Для этой модели существует K = 7 параметров (d = 6 членов точки пересечения и наклон).

Предположим, что вектор параметров расположен следующим образом

В этом случае первая матрица проекта для года 1 выглядит как

и вторая матрица проекта для года 2 выглядит как

Матрицы проекта для остальных 4 лет аналогичны.

K = 7; N = n*d;
X = cell(n,1);
for i = 1:n
    x0 = zeros(d,K-1);
    x0(:,i) = 1;
    X{i} = [x0,x(i:n:N)];
end

Подгонка модели.

Подгонка модели с помощью обыкновенных наименьших квадратов (OLS).

[b,sig,E,V] = mvregress(X,Y,'algorithm','cwls');
b

b =

   41.6878
   26.1864
  -64.5107
   11.0924
  -59.1872
   71.3313
    4.9525

Постройте график подобранной модели.

xx = linspace(min(x),max(x));
axx = repmat(b(1:K-1),1,length(xx));
bxx = repmat(b(K)*xx,n,1);
yhat =  axx + bxx;

figure()
hPoints = gscatter(x,y,year);
hold on
hLines = plot(xx,yhat);
for i=1:n  
   set(hLines(i),'color',get(hPoints(i),'color'));
end
hold off

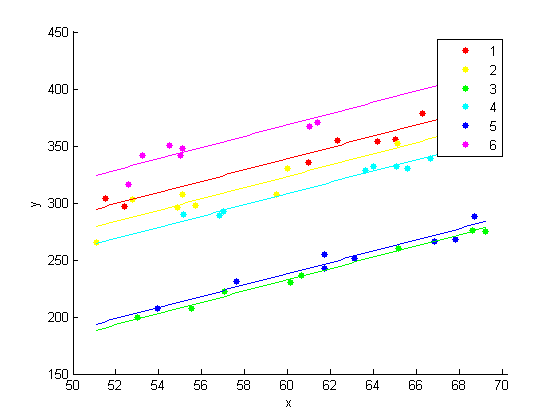
Модель с специфическими для года точками пересечения и общим наклоном, по-видимому, вполне соответствует данным.

Остаточная корреляция.

Постройте график невязок, сгруппированных по годам.

figure()
gscatter(year,E(:),city)
ylabel('Residuals')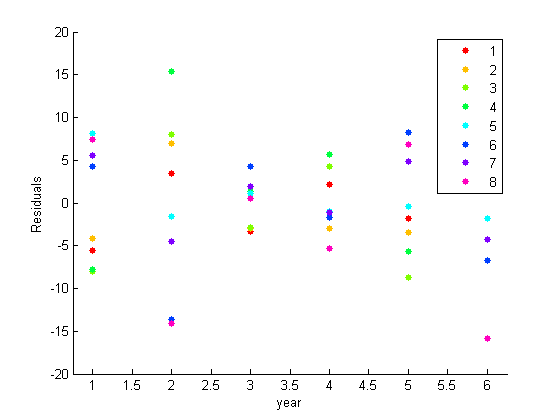

Остаточный график предполагает наличие параллельной корреляции. Для примеров города 1, 2, 3 и 4 постоянно выше или ниже среднего значения как группа в любой данный год. То же самое относится и к набору городов 5, 6, 7 и 8. Как видно из исследовательских графиков, нет никаких систематических специфических для города эффектов.

Панель исправила стандартные ошибки.

Используйте предполагаемую дисперсионно-ковариационную матрицу ошибок, чтобы вычислить стандартные ошибки, исправленные панелью, для коэффициентов регрессии.

XX = cell2mat(X);
S = kron(eye(n),sig);
Vpcse = inv(XX'*XX)*XX'*S*XX*inv(XX'*XX);
se = sqrt(diag(Vpcse))

se =

    9.3750
    8.6698
    9.3406
    9.4286
    9.5729
    8.8207
    0.1527