Для подгонки многомерной линейной регрессионой модели с использованием mvregressнеобходимо настроить матрицу отклика и разработать матрицы определенным способом. Учитывая правильно отформатированные входы, mvregress может справиться с множеством многомерных регрессионных задач.
mvregress ожидает, что n наблюдения потенциально коррелированных d -мерных откликов будут в матрице n -by- d с именем Y, для примера. То есть настройте свои ответы так, чтобы структура зависимостей была между наблюдениями в одной строке. Если вы задаете Y как вектор длины n (строка или вектор-столбец), затем mvregress принимает, что d = 1, и рассматривает элементы как n независимые наблюдения. Он не моделирует вектор как одну реализацию коррелированного ряда (такие как временные ряды).
Чтобы проиллюстрировать, как настроить матрицу отклика, предположим, что ваши многомерные отклики являются повторными измерениями, выполненными на субъектах в нескольких временных точках, как на следующем рисунке.
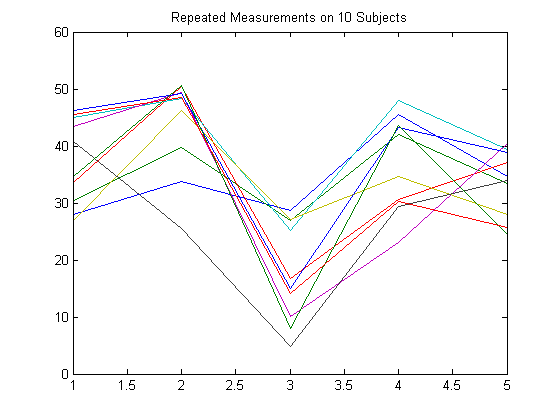
Предположим, что наблюдения внутри субъекта коррелируют.
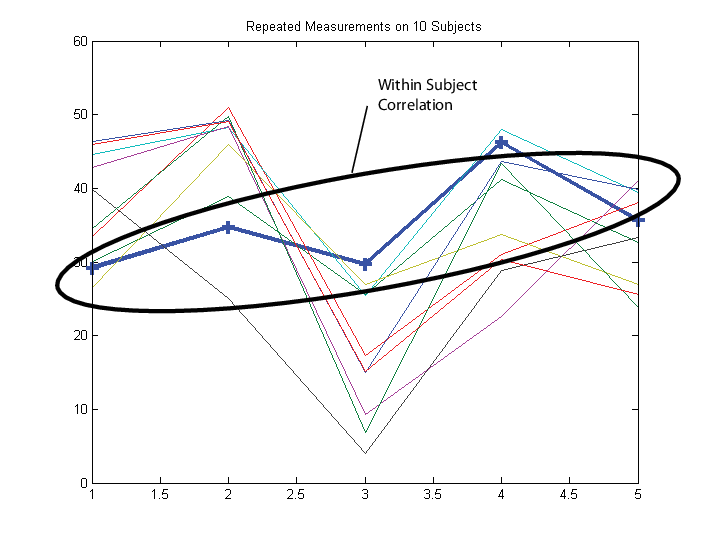
В этом случае настройте матрицу отклика Y таким образом, каждая строка соответствует субъекту, а каждый столбец соответствует временной точке.

Затем снова предположим, что наблюдения, сделанные на субъектах в то же время, коррелируются (параллельная корреляция).
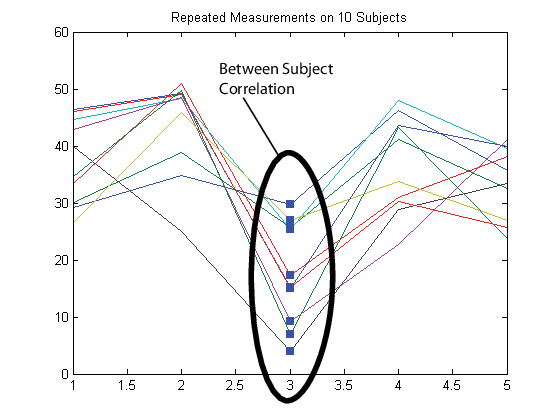
В этом случае настройте матрицу отклика Y таким образом, каждая строка соответствует временной точке, и каждый столбец соответствует субъекту.
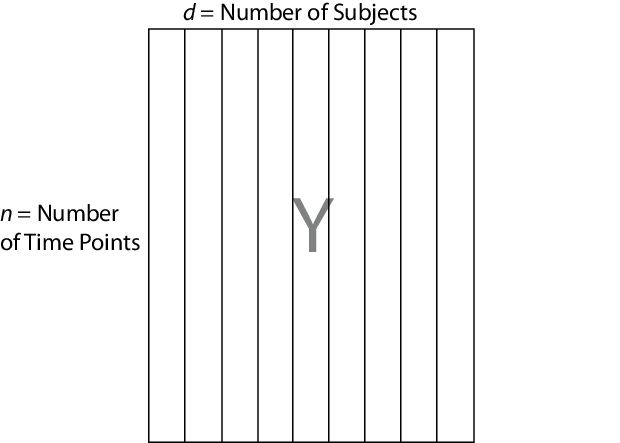
В многомерной линейной регрессионной модели каждая d -мерная характеристика имеет соответствующую матрицу проекта. В зависимости от модели матрица проекта может состоять из переменных экзогенного предиктора, фиктивных переменных, отстающих ответов или комбинации этих и других ковариационных терминов.
Если d > 1 и все d размерности имеют одинаковую матрицу проекта, задайте одну матрицу n -by p design, где p количество переменных предиктора. Чтобы определить точку пересечения для каждой размерности, добавьте столбец с таковыми в матрицу проекта. В этом случае,mvregress применяет матрицу проекта ко всем d размерностям.
Если d > 1 и все d размерности не имеют одинаковой матрицы проекта, задайте матрицы проекта с помощью массива ячеек n d -by K arrays с именем X, для примера. K - общее количество коэффициентов регрессии в модели. Обратите внимание, что строки массивов в X соответствуют столбцам матрицы отклика, Y.
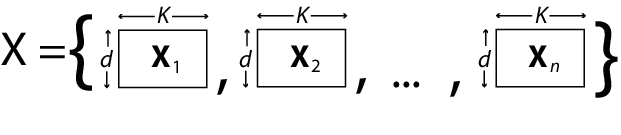
Если все n наблюдения имеют одну и ту же матрицу проекта, можно задать массив ячеек, содержащий одну матрицу d -by K design. В этом случае mvregress применяет матрицу проекта ко всем n наблюдениям. Для примера эта ситуация может возникнуть, если предикторы являются функциями времени, и все наблюдения были измерены одновременно точки.
В частном случае, когда d = 1, можно задать одну матрицу n -by K проекта (не в массиве ячеек). Тем не менее, вы должны рассмотреть использование fitlm для подгонки регрессионных моделей к одномерным, непрерывным реакциям.
Следующие разделы иллюстрируют, как настроить некоторые общие многомерные регрессионые задачи для оценки с помощью mvregress.
Многомерная общая линейная модель имеет вид
В расширенном виде,
То есть каждый d -мерный ответ имеет переменные точки пересечения и p предиктора, и каждая размерность имеет свой собственный набор коэффициентов регрессии. В этой форме решение методом наименьших квадратов B = X\Y. Чтобы оценить эту модель с помощью mvregress, используйте n -by - d матрицу ответов, как описано выше.
Если все d размерности имеют одинаковую матрицу проекта, используйте n матрицу проекта -by- (p + 1), как выше. Добавление столбца таковых к переменным предиктора p вычисляет точку пересечения для каждой размерности.
Если все d размерности не имеют той же матрицы проекта, переформатировали n (p + 1), проектируют матрицу в длину - n массив ячеек d K матрицами. Здесь K = (p + 1) d для точки пересечения и склонов для каждой размерности.
Для примера предположим, что n = 4, d = 3 и p = 2 (два предиктора в сложение к точке пересечения). Этот рисунок показывает, как форматировать i-й элемент массива ячеек.
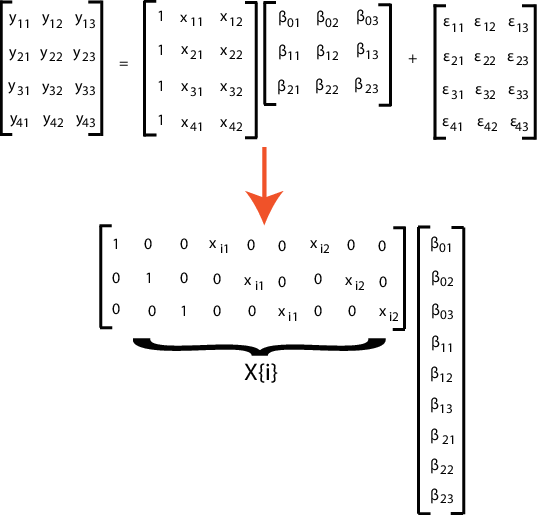
Если вы предпочитаете, можно перестроить вектор коэффициентов K -на-1 назад в (p + 1) -by - d матрицу после оценки.
Чтобы наложить ограничения на параметры модели, скорректируйте матрицу проекта соответственно. Например, предположим, что три размерности в предыдущем примере имеют общий уклон. То есть, и В этом случае каждая матрица проекта является 3 на 5, как показано на следующем рисунке.
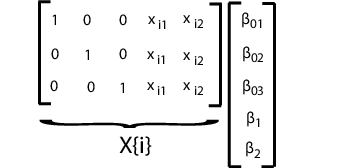
В продольном анализе можно измерить ответы на n субъекты в d временных точек с корреляцией между наблюдениями, сделанными по той же теме. Для примера предположим, что вы измеряете ответы yij в моменты времени tij, i = 1,..., n и j = 1,..., d. Кроме сложения, предположим, что каждый субъект находится в одной из двух групп (таких как мужчина или женщина), заданных переменной показателя Gi. Можно смоделировать yij как функцию Gi и tij с групповыми точками пересечения и склонами следующим образом:
где
Большинство продольных моделей включают время как явный предиктор.
Чтобы подогнать эту модель используя mvregress, расположите ответы в матрице n -by d, где n - количество субъектов и d - количество временных точек. Задайте матрицы проекта в n массиве ячеек -length из d -by - K матриц, где здесь K = 4 для четырех коэффициентов регрессии.
Для примера предположим d = 5 (пять наблюдений на субъекта). i матрица проекта и соответствующий вектор параметра для указанной модели показаны на следующем рисунке.
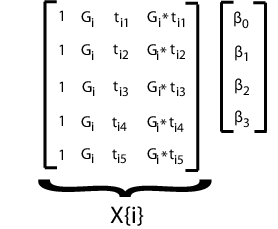
В панель анализе можно измерить ответы и ковариаты по d субъектам (таким как индивидуумы или страны) в n времени точек. Для примера предположим, что вы измеряете ответы ytj и ковариаты, xtj на субъектах j = 1,..., d временами t = 1,..., n. Модель панели фиксированных эффектов с специфическими для субъекта фиксированными эффектами и параллельной корреляцией может выглядеть следующим образом:
где
В отличие от продольных моделей, модель панельного анализа обычно включает ковариаты, измеренные в каждой временной точке, вместо использования времени в качестве явного предиктора.
Чтобы подогнать эту модель используя mvregress, расположите ответы в n -by - d матрице, так что каждый столбец соответствует субъекту. Задайте матрицы проекта в n массиве ячеек -length из d K матриц, где here K = d + 1 для перехвата d и члена наклона.
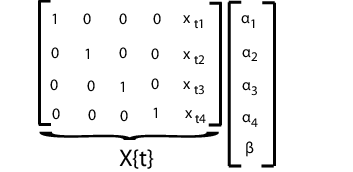
Например, предположим d = 4 (четыре субъекта). t матрица проекта и соответствующий вектор параметра показаны на следующем рисунке.
В, казалось бы, несвязанной регрессии (SUR), вы моделируете d отдельные регрессии, каждый со своими собственными точками пересечения и наклоном, но общей дисперсионно-ковариационной матрицей ошибок. Для примера предположим, что вы измеряете ответы yij и ковариаты, xij для регрессионых моделей j = 1,..., d, с i = 1,..., n наблюдениями, чтобы соответствовать каждой регрессии. Модель SUR может выглядеть следующим образом:
где
Эта модель очень похожа на многомерную общую линейную модель, за исключением того, что она имеет различные ковариаты для каждой размерности.
Чтобы подогнать эту модель используя mvregress, расположите ответы в матрице n -by d, так что каждый столбец имеет данные для j-й регрессионой модели. Задайте матрицы проекта в n массиве ячеек -length из d K матриц, где здесь K = 2 d для d перехватов и d склонов.
Например, предположим d = 3 (три регрессии). i матрица проекта и соответствующий вектор параметра показаны на следующем рисунке.
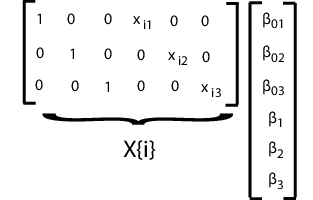
Векторная авторегрессионная модель VAR (p) выражает d -мерные отклики временных рядов как линейную функцию p отстающих d -мерных откликов от предыдущих раз. Для примера предположим, что вы измеряете ответы, ytj для временных рядов j = 1,..., d временами t = 1,..., n. Модель VAR (p) может выглядеть следующим образом:
где
При оценке векторных авторегрессивных моделей вам обычно нужно использовать первые p наблюдения, чтобы инициировать модель или предоставить некоторые другие предварительные значения отклика.
Чтобы подогнать эту модель используя mvregress, расположите отклики в матрице n -by d, так что каждый столбец соответствует временному ряду. Задайте матрицы проекта в n массиве ячеек -length из d -by- K матриц, где here K = d + pd2.
Для примера предположим, что d = 2 (два временных рядов) и p = 1 (одна задержка). t матрица проекта и соответствующий вектор параметра показаны на следующем рисунке.
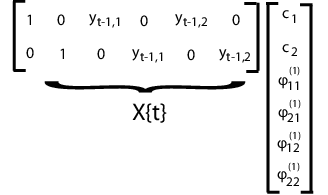
Кроме того, Econometrics Toolbox™ имеет функции для подбора кривой и прогнозирования моделей VAR (p), включая опцию для задания переменных экзогенного предиктора.