Решение дифференциальных уравнений с использованием преобразования Лапласа

Решить дифференциальные уравнения при помощи преобразований Лапласа в Symbolic Math Toolbox™ с этим рабочим процессом. Для простых примеров преобразования Лапласа см. laplace и ilaplace.

Определение: Преобразование Лапласа

Преобразование Лапласа функции f (t) является

$F (s) = \int_{0}^{\infty} f (t) e^{- t s} d t .$

Концепция: Использование символьных рабочих процессов

Символьные рабочие процессы сохраняют вычисления в естественной символьной форме вместо числовой формы. Этот подход помогает вам понять свойства вашего решения и использовать точные символические значения. Вы подставляете числа вместо символьных переменных только тогда, когда вам требуется числовой результат или вы не можете продолжать символьно. Для получения дополнительной информации смотрите Выбрать числовую или символьную арифметику. Как правило, шаги следующие:

Объявить уравнения.
Решить уравнения.
Подстановочные значения.
Постройте график результатов.
Анализ результатов.

Рабочий процесс: Решение схемы RLC с использованием преобразования Лапласа

Объявить уравнения

Можно использовать преобразование Лапласа, чтобы решить дифференциальные уравнения с начальными условиями. Для примера можно решить цепи сопротивление-индуктор-конденсатор (RLC), такие как эта схема.

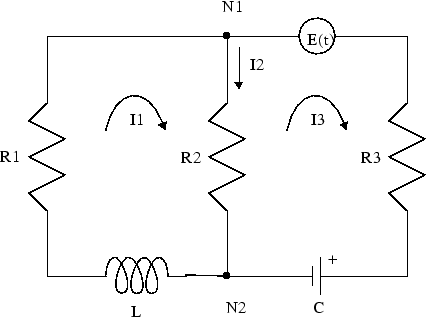
Сопротивления в оме: _R1, _R2, _R3
Токи в ампере: _I1, _I2, _I3
Индуктивность в Генри: L
Емкость в фараде: C
Электродвижущая сила в вольтах: E (t)
Заряд в кулоне: Q (t)

Примените законы напряжения и тока Кирхгофа, чтобы получить дифференциальные уравнения для схемы RLC.

$\frac{d I_{1}}{d t} + \frac{R_{2}}{L} \frac{d Q}{d t} = \frac{R_{2} - R_{1}}{L} I_{1} .$

$\frac{d Q}{d t} = \frac{1}{R_{3} + R_{2}} (E (t) - \frac{1}{C} Q (t)) + \frac{R_{2}}{R_{3} + R_{2}} I_{1} .$

Объявите переменные. Поскольку физические величины имеют положительные значения, задайте соответствующие допущения для переменных. Предположим, E (t) будет переменным напряжением 1 В.

syms L C I1(t) Q(t) s
R = sym('R%d',[1 3]);
assume([t L C R] > 0)
E(t) = 1*sin(t);        % Voltage = 1 V

Объявить дифференциальные уравнения.

dI1 = diff(I1,t);
dQ = diff(Q,t);
eqn1 = dI1 + (R(2)/L)*dQ == (R(2)-R(1))/L*I1
eqn2 = dQ == (1/(R(2)+R(3))*(E-Q/C)) + R(2)/(R(2)+R(3))*I1

eqn1(t) =
diff(I1(t), t) + (R2*diff(Q(t), t))/L == -(I1(t)*(R1 - R2))/L
eqn2(t) =
diff(Q(t), t) == (sin(t) - Q(t)/C)/(R2 + R3) + (R2*I1(t))/(R2 + R3)

Предположим, что начальный ток и заряд, _I0 и _Q0, являются 0. Объявите эти начальные условия.

cond1 = I1(0) == 0
cond2 = Q(0) == 0

cond1 =
I1(0) == 0
cond2 =
Q(0) == 0

Решение уравнений

Вычислите преобразование Лапласа eqn1 и eqn2.

eqn1LT = laplace(eqn1,t,s)
eqn2LT = laplace(eqn2,t,s)

eqn1LT =
s*laplace(I1(t), t, s) - I1(0) - (R2*(Q(0) - s*laplace(Q(t), t, s)))/L == ...
-((R1 - R2)*laplace(I1(t), t, s))/L
eqn2LT =
s*laplace(Q(t), t, s) - Q(0) == (R2*laplace(I1(t), t, s))/(R2 + R3) + ...
(C/(s^2 + 1) - laplace(Q(t), t, s))/(C*(R2 + R3))

Функция solve решает только для символьных переменных. Поэтому использовать solve, первая замена laplace(I1(t),t,s) и laplace(Q(t),t,s) с переменными I1_LT и Q_LT.

syms I1_LT Q_LT
eqn1LT = subs(eqn1LT,[laplace(I1,t,s) laplace(Q,t,s)],[I1_LT Q_LT])

eqn1LT =
I1_LT*s - I1(0) - (R2*(Q(0) - Q_LT*s))/L == -(I1_LT*(R1 - R2))/L

eqn2LT = subs(eqn2LT,[laplace(I1,t,s) laplace(Q,t,s)],[I1_LT Q_LT])

eqn2LT =
Q_LT*s - Q(0) == (I1_LT*R2)/(R2 + R3) - (Q_LT - C/(s^2 + 1))/(C*(R2 + R3))

Решите уравнения для I1_LT и Q_LT.

eqns = [eqn1LT eqn2LT];
vars = [I1_LT Q_LT];
[I1_LT, Q_LT] = solve(eqns,vars)

I1_LT =
(R2*Q(0) + L*I1(0) - C*R2*s + L*s^2*I1(0) + R2*s^2*Q(0) + C*L*R2*s^3*I1(0) + ...
C*L*R3*s^3*I1(0) + C*L*R2*s*I1(0) + C*L*R3*s*I1(0))/((s^2 + 1)*(R1 - R2 + L*s + ...
C*L*R2*s^2 + C*L*R3*s^2 + C*R1*R2*s + C*R1*R3*s - C*R2*R3*s))
Q_LT =
(C*(R1 - R2 + L*s + L*R2*I1(0) + R1*R2*Q(0) + R1*R3*Q(0) - R2*R3*Q(0) + ...
L*R2*s^2*I1(0) + L*R2*s^3*Q(0) + L*R3*s^3*Q(0) + R1*R2*s^2*Q(0) + R1*R3*s^2*Q(0) - ...
R2*R3*s^2*Q(0) + L*R2*s*Q(0) + ...
L*R3*s*Q(0)))/((s^2 + 1)*(R1 - R2 + L*s + C*L*R2*s^2 + C*L*R3*s^2 + ...
                C*R1*R2*s + C*R1*R3*s - C*R2*R3*s))

Вычислите _I1 и Q путем вычисления обратного преобразования Лапласа I1_LT и Q_LT. Упростите результат. Подавить выход, потому что он длинный.

I1sol = ilaplace(I1_LT,s,t);
Qsol = ilaplace(Q_LT,s,t);
I1sol = simplify(I1sol);
Qsol = simplify(Qsol);

Подстановочные значения

Перед построением графика результатов замените символьные переменные числовыми значениями элементов схемы. Предположим R 1 = 4 , R2 = 2 , R3 = 3 , C = 1/4 F, L = 1,6 H, I1 (0) = 15 A и Q (0) = 2 C.

vars = [R L C I1(0) Q(0)];
values = [4 2 3 1.6 1/4 15 2];
I1sol = subs(I1sol,vars,values)
Qsol = subs(Qsol,vars,values)

I1sol =
15*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) - ...
        (293*1001^(1/2)*sinh((1001^(1/2)*t)/40))/21879) - (5*sin(t))/51
Qsol =
(4*sin(t))/51 - (5*cos(t))/51 + (107*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) + ...
        (2039*1001^(1/2)*sinh((1001^(1/2)*t)/40))/15301))/51

Графическое изображение результатов

Постройте график текущей I1sol и заряжать Qsol. Покажите как переходное, так и статическое поведение с помощью двух различных временных интервалов: 0 ≤ t ≤ 10 и 5 ≤ t ≤ 25.

subplot(2,2,1)
fplot(I1sol,[0 10])                      
title('Current')
ylabel('I1(t)')
xlabel('t')

subplot(2,2,2)
fplot(Qsol,[0 10])                        
title('Charge')
ylabel('Q(t)')
xlabel('t')

subplot(2,2,3)
fplot(I1sol,[5 25])                  
title('Current')
ylabel('I1(t)')
xlabel('t')
text(7,0.25,'Transient')
text(16,0.125,'Steady State')

subplot(2,2,4)
fplot(Qsol,[5 25])                        
title('Charge')
ylabel('Q(t)')
xlabel('t')
text(7,0.25,'Transient')
text(15,0.16,'Steady State')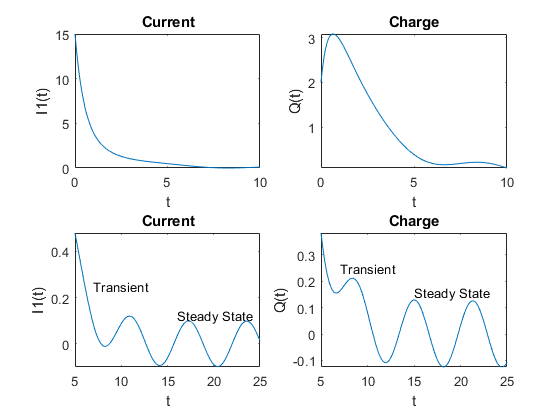

Анализ результатов

Первоначально ток и заряд уменьшаются экспоненциально. Однако в долгосрочной перспективе они являются колебательными. Это поведение называется «переходным» и «устойчивым состоянием», соответственно. С помощью символического результата можно проанализировать свойства результата, что невозможно с числовыми результатами.

Визуальный осмотр I1sol и Qsol. Они являются суммой терминов. Найти условия при помощи children. Затем найдите вклады терминов, построив их над [0 15]. Графики показывают переходные и устойчивые состояния условия.

I1terms = children(I1sol);
Qterms = children(Qsol);

subplot(1,2,1)
fplot(I1terms,[0 15])
ylim([-2 2])
title('Current terms')

subplot(1,2,2)
fplot(Qterms,[0 15])
ylim([-2 2])
title('Charge terms')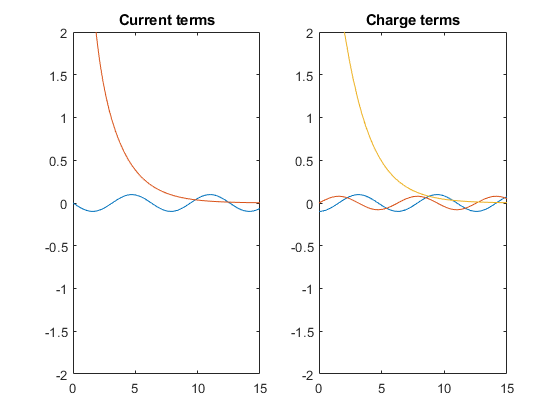

Графики показывают, что I1sol имеет переходный и установившийся термин, в то время как Qsol имеет переходный и два устойчивых состояния срока. При визуальном осмотре заметьте I1sol и Qsol иметь термин, содержащий exp функция. Предположим, что этот термин вызывает переходный экспоненциальный распад. Разделите переходные и устойчивые состояния условия в I1sol и Qsol проверяя условия для exp использование has.

I1transient = I1terms(has(I1terms,'exp'))
I1steadystate = I1terms(~has(I1terms,'exp'))

I1transient =
15*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) - (293*1001^(1/2)*sinh((1001^(1/2)*t)/40))/21879)
I1steadystate =
-(5*sin(t))/51

Точно так же разделите Qsol в переходные и установившиеся состояния. Этот результат демонстрирует, как символические вычисления помогают вам анализировать свою задачу.

Qtransient = Qterms(has(Qterms,'exp'))
Qsteadystate = Qterms(~has(Qterms,'exp'))

Qtransient =
(107*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) + (2039*1001^(1/2)*sinh((1001^(1/2)*t)/40))/15301))/51
Qsteadystate =
[ -(5*cos(t))/51, (4*sin(t))/51]

Документация