Поскольку CWT является избыточным преобразованием, и коэффициенты CWT зависят от вейвлета, может быть трудно интерпретировать результаты.
Чтобы помочь вам в интерпретации коэффициентов CWT, лучше всего начать с простого сигнала для анализа и анализирующего вейвлета с простой структурой.
Сигнальной функцией, что вейвлеты очень хороши в обнаружении, является разрыв или особенность. Резкие переходы в сигналах результата в коэффициентах вейвлета с большими абсолютными значениями.
Для сигнала создайте сдвинутый импульс. Импульс происходит в точке 500.
x = zeros(1000,1); x(500) = 1;
Для вейвлета выберите вейвлет Haar.
[~,psi,xval] = wavefun('haar',10);
plot(xval,psi); axis([0 1 -1.5 1.5]);
title('Haar Wavelet');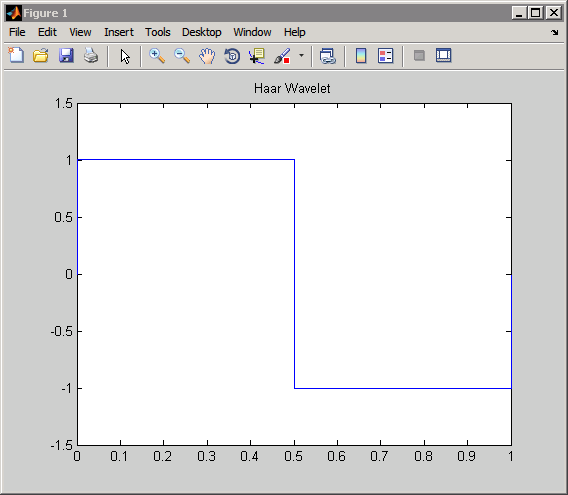
Чтобы вычислить CWT с помощью вейвлета Haar в шкалах от 1 до 128, введите:
CWTcoeffs = cwt(x,1:128,'haar');
CWTcoeffs является 128 на 1000 матрицей. Каждая строка матрицы содержит коэффициенты CWT для одной шкалы. Существует 128 строк, потому что SCALES вход в cwt является 1:128. Размерность столбца матрицы соответствует длине входного сигнала.
Напомним, что CWT сигнала 1D является функцией от параметров шкалы и положения. Чтобы создать график коэффициентов CWT, постройте график положения вдоль оси x, масштабируйте вдоль оси y и закодируйте величину или размер коэффициентов CWT как цвет в каждой точке x-y или плоскости шкалы времени.
Вы можете создать этот график, используя cwt с необязательным входным параметром 'plot'.
cwt(x,1:128,'haar','plot'); colormap jet; colorbar;
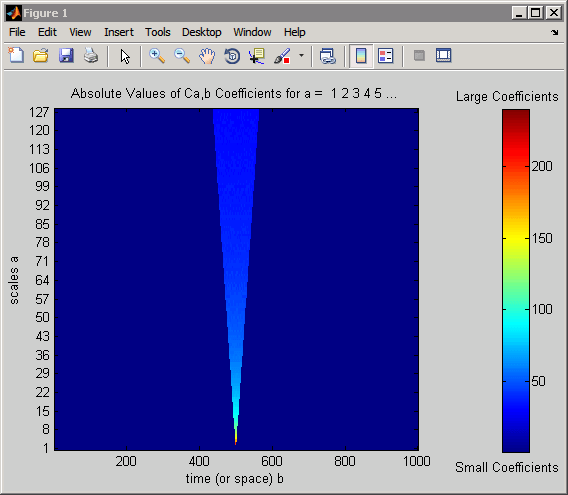
Предыдущий рисунок был изменен текстовыми метками, чтобы явным образом показать, какие цвета указывают на большие и маленькие коэффициенты CWT.
Можно также построить график размера коэффициентов CWT в 3D с
cwt(x,1:64,'haar','3Dplot'); colormap jet;
Исследуя CWT сдвинутого импульсного сигнала, можно увидеть, что набор больших коэффициентов CWT сконцентрирован в узкой области во временной плоскости в малых шкалах с центром вокруг точки 500. Когда шкала увеличивается, набор больших коэффициентов CWT становится шире, но остается с центром вокруг точки 500. Если проследить границу этой области, она напоминает следующий рисунок.
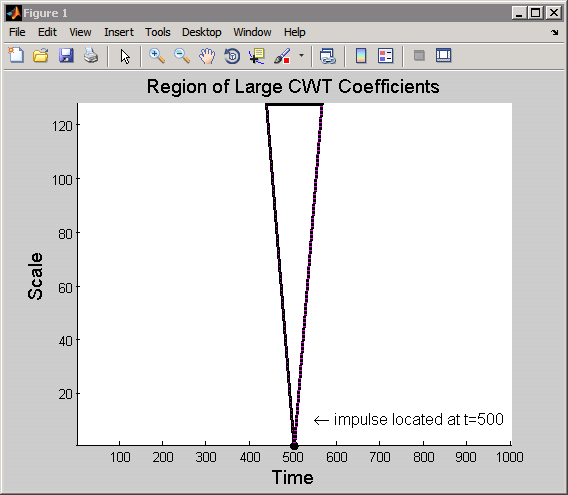
Эта область упоминается как конус влияния точки t = 500 для вейвлета Хаара. Для заданной точки конус влияния показывает вам, на какие коэффициенты CWT влияет значение сигналов в этой точке.
Чтобы понять конус влияния, предположим, что у вас есть вейвлет, поддерживаемый [- C, C]. Смещение вейвлета по b и масштабирование по a приводит к вейвлету, поддерживаемому [- Ca+b, Ca+b]. Для простого случая сдвинутого импульса,Коэффициенты CWT являются только ненулевыми в интервале вокруг и равны поддержке вейвлета в каждой шкале. Вы можете увидеть это, рассматривая формальное выражение CWT сдвинутого импульса.
Для импульса коэффициенты CWT равны сопряженному, обращенному во времени и масштабированному вейвлету как функции параметра shift, b. Вы можете увидеть это, построив график коэффициентов CWT для нескольких выбранных шкал.
subplot(311)
plot(CWTcoeffs(10,:)); title('Scale 10');
subplot(312)
plot(CWTcoeffs(50,:)); title('Scale 50');
subplot(313)
plot(CWTcoeffs(90,:)); title('Scale 90');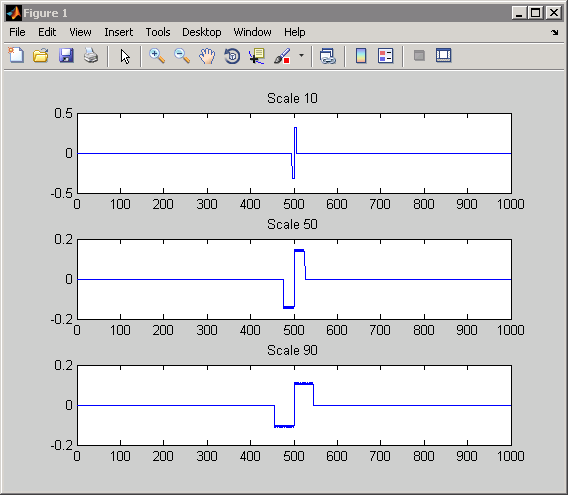
Конус влияния зависит от вейвлета. Вы можете найти и построить график конуса влияния для определенного вейвлета с conofinf.
Следующий пример показывает суперпозицию двух сдвинутых импульсов, . В этом случае используйте экстремальный вейвлет фазы Daubechies с четырьмя моментами исчезновения db4. Следующий рисунок показывает конус влияния для точек 300 и 500, используя db4 вейвлет.
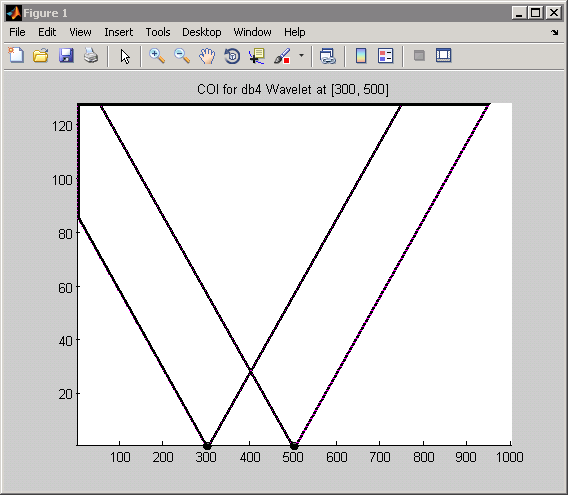
Посмотрите на точку 400 для шкалы 20. В этой шкале можно увидеть, что ни один из конусов влияния не перекрывает точку 400. Поэтому можно ожидать, что коэффициент CWT будет нулем в этой точке и шкале. Сигнал является только ненулевым при двух значениях, 300 и 500, и ни один из конусов влияния для этих значений не включает точку 400 в шкале 20. Подтвердить это можно путем ввода:
x = zeros(1000,1); x([300 500]) = 1; CWTcoeffs = cwt(x,1:128,'db4'); plot(CWTcoeffs(20,:)); grid on;
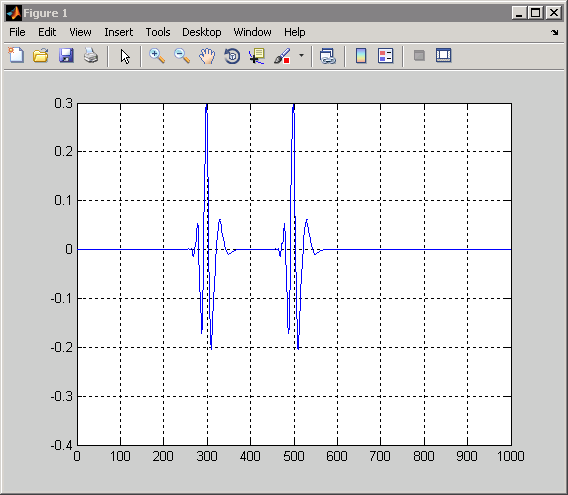
Далее рассмотрим точку 400 по шкале 80. В шкале 80 конусы влияния для обеих точек 300 и 500 включают точку 400. Даже если сигнал равен нулю в точке 400, вы получаете ненулевой коэффициент CWT в этой шкале. Коэффициент CWT ненулевый, потому что поддержка вейвлет стала достаточно большой в этой шкале, чтобы позволить значениям сигналов на 100 баллов выше и ниже влиять на коэффициент CWT. Подтвердить это можно путем ввода:
plot(CWTcoeffs(80,:)); grid on;
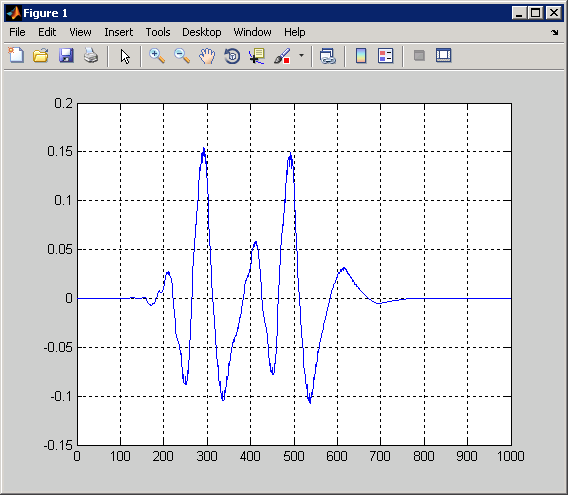
В предыдущем примере коэффициенты CWT стали большими вблизи резкого изменения сигнала. Эта способность обнаруживать разрывы является силой вейвлет. Предыдущий пример также продемонстрировал, что коэффициенты CWT локализуют разрыв лучше всего в малых шкалах. В малых шкалах небольшая поддержка вейвлета гарантирует, что особенность влияет только на небольшой набор вейвлет-коэффициентов.
Чтобы продемонстрировать, почему вейвлет преобразования настолько опытна в обнаружении резких изменений в сигнале, рассмотрим сдвинутый сигнал Heaviside, или модуль шаговый сигнал.
x = [zeros(500,1); ones(500,1)]; CWTcoeffs = cwt(x,1:64,'haar','plot'); colormap jet;
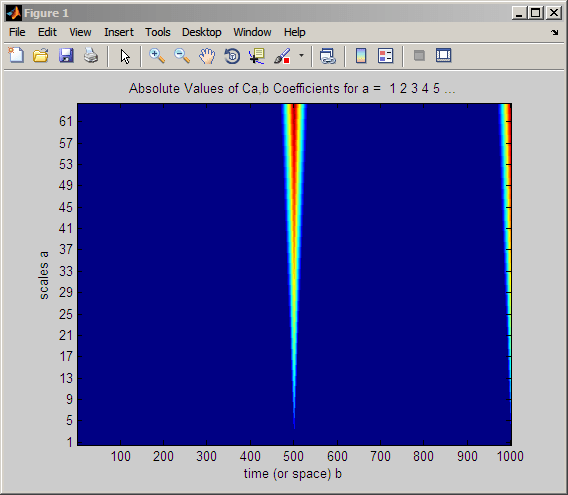
Подобно примеру сдвинутого импульса, резкий переход в функции сдвинутого шага приводит к большим коэффициентам CWT с разрывом. Следующий рисунок иллюстрирует, почему это происходит.
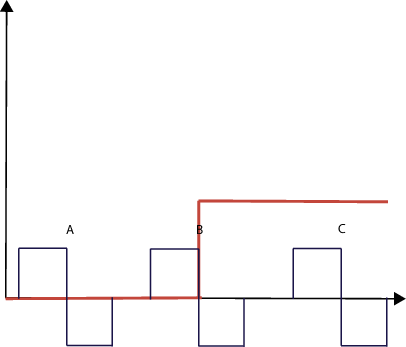
На предыдущем рисунке красная функция является функцией сдвинутого единичного шага. Черные функции, обозначенные A, B и C, изображают вейвлеты Хаара в той же шкале, но в разных положениях. Можно увидеть, что коэффициенты CWT вокруг положения A равны нулю. Сигнал равен нулю в этой окрестности, и, следовательно, преобразование также равняется нулю, потому что любой вейвлет интегрируется в ноль.
Обратите внимание, что вейвлет Haar с центром вокруг положения B. Отрицательная часть вейвлета Haar перекрывается с областью функции шага, которая равна 1. Коэффициенты CWT отрицательны, потому что продукт вейвлета Haar и единичного шага является отрицательной константой. Интегрирование по этой области приводит к отрицательному числу.
Обратите внимание на вейвлет Haar, центрированный вокруг положения C. Здесь коэффициенты CWT равны нулю. Шаговая функция равна единице. Продукт вейвлета с функцией шага равен вейвлет. Интеграция любого вейвлета над его поддержкой равна нулю. Это свойство нулевого момента вейвлетов.
В положении B вейвлет Haar уже сместился в ненулевой фрагмент шаговой функции на 1/2 ее поддержки. Как только поддержка вейвлета пересекается с фрагментом единицы функции шага, коэффициенты CWT являются ненулевыми. Фактически, ситуация, проиллюстрированная на предыдущем рисунке, совпадает с коэффициентами CWT, достигающими своего наибольшего абсолютного значения. Это связано с тем, что все отрицательное отклонение колебаний вейвлета перекрывается с фрагментом единства единичного шага, в то время как ни одно из положительных отклонений вейвлета не происходит. Когда вейвлет переключается на точку, в которой положительное отклонение перекрывается с модулем шагом, будет некоторый положительный вклад в интеграл. Вейвлет все еще отрицательны (отрицательный фрагмент интеграла больше по площади), но они меньше по абсолютному значению, чем те, что получают в положении B.
Следующий рисунок иллюстрирует два других положения, где вейвлет пересекает фрагмент единства единичного шага.
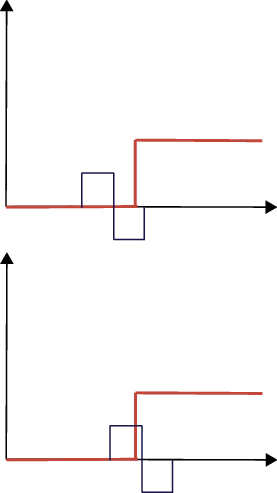
На верхнем рисунке вейвлет только начал перекрываться с фрагментом единицы модуля единичного шага. В этом случае коэффициенты CWT отрицательны, но не такие большие по абсолютному значению, как коэффициенты, полученные в положении B. На нижнем рисунке вейвлет сдвинулся прошлое положение B и положительное отклонение вейвлета начинает вносить вклад в интеграл. Коэффициенты CWT все еще отрицательны, но не такие большие по абсолютному значению, как коэффициенты, полученные в положении B.
Теперь можно визуализировать, как вейвлет преобразования способен обнаруживать разрывы. Можно также визуализировать в этом простом примере, почему коэффициенты CWT отрицательны в CWT сдвинутого шага модуля, используя вейвлет Haar. Обратите внимание, что это поведение отличается для других вейвлетов.
x = [zeros(500,1); ones(500,1)];
CWTcoeffs = cwt(x,1:64,'haar','plot'); colormap jet;
% plot a few scales for visualization
subplot(311);
plot(CWTcoeffs(5,:)); title('Scale 5');
subplot(312);
plot(CWTcoeffs(10,:)); title('Scale 10');
subplot(313);
plot(CWTcoeffs(50,:)); title('Scale 50');Затем рассмотрим, как CWT представляет гладкие сигналы. Поскольку синусоидальные колебания являются общим явлением, в этом разделе рассматривается, как синусоидальные колебания в сигнале влияют на коэффициенты CWT. Для начала рассмотрим sym4 вейвлет в определенной шкале, наложенной на синусоиду.
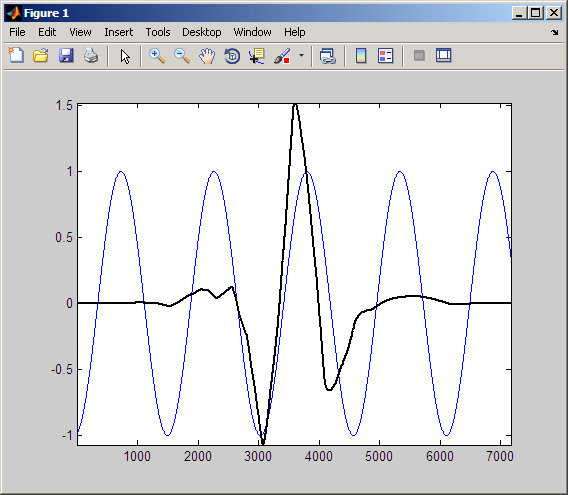
Напомним, что коэффициенты CWT получаются путем вычисления продукта сигнала со сдвинутым и масштабированным анализирующим вейвлетом и интегрирования результата. Следующие рисунки показывают продукт вейвлета и синусоиды с предыдущего рисунка.
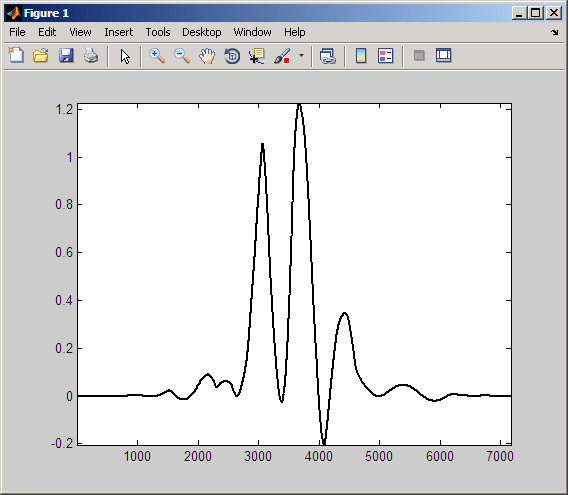
Можно видеть, что интеграция по этому продукту создает положительный коэффициент CWT. Это происходит потому, что колебание в вейвлете приблизительно совпадает с периодом синусоиды. Вейвлет находится в фазе с синусоидой. Отрицательные отклонения вейвлета примерно совпадают с отрицательными отклонениями синусоиды. То же самое относится и к положительным отклонениям как вейвлет, так и синусоида.
Следующий рисунок смещает вейвлет на 1/2 периода синусоиды.
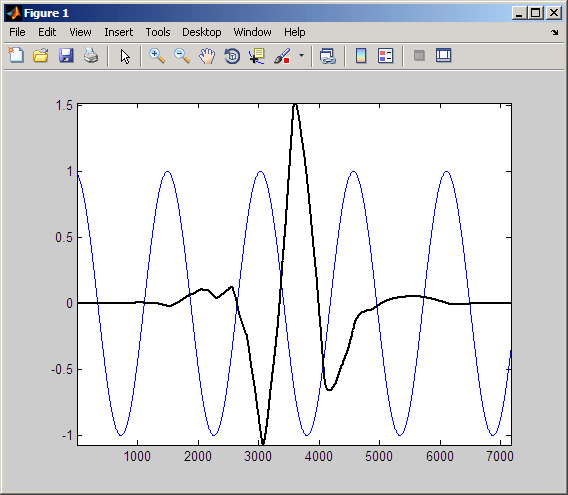
Исследуйте продукт сдвинутого вейвлета и синусоиды.
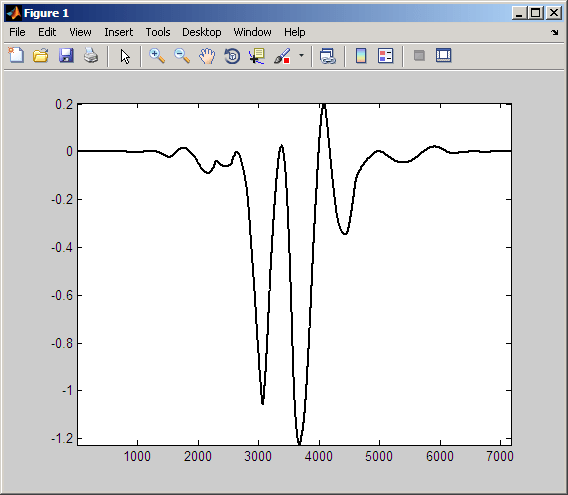
Можно увидеть, что интеграция по этому продукту создает отрицательный коэффициент CWT. Это происходит, потому что вейвлет находится в 1/2 цикла вне фазы с синусоидой. Отрицательные отклонения вейвлета примерно совпадают с положительными отклонениями синусоиды. Положительные отклонения вейвлета примерно совпадают с отрицательными отклонениями синусоиды.
Наконец, сдвиньте вейвлет приблизительно на одну четверть цикла синусоиды.
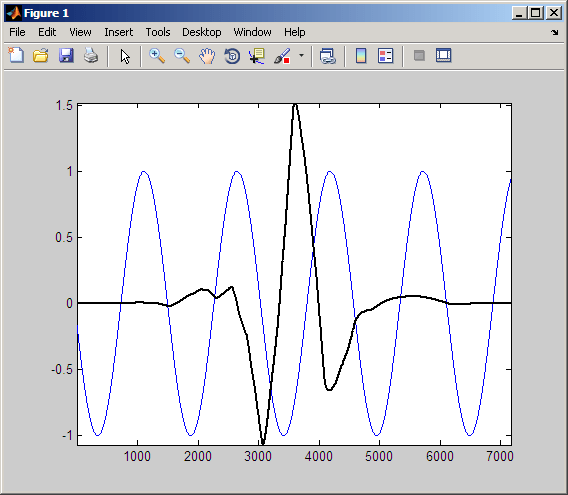
Следующий рисунок показывает продукт сдвинутого вейвлета и синусоиды.
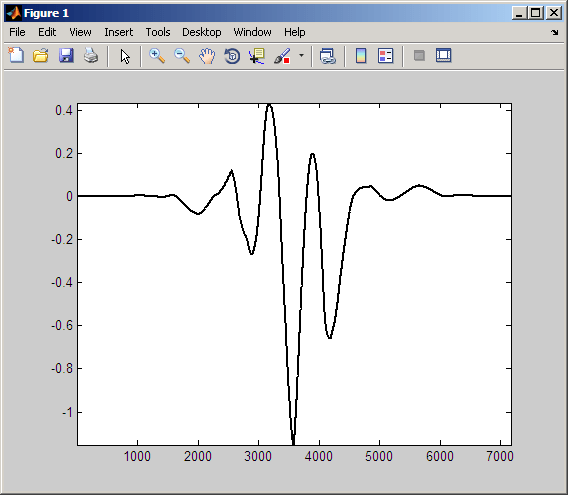
Интеграция по этому продукту создает коэффициент CWT, намного меньший по абсолютному значению, чем в любом из двух предыдущих примеров. Это происходит потому, что отрицательное отклонение вейвлета приблизительно выравнивается с положительным отклонением синусоиды. Кроме того, основное положительное отклонение вейвлета приблизительно совпадает с положительным отклонением синусоиды. Полученный продукт выглядит гораздо больше как вейвлет, чем два других продукта. Если бы это выглядело точно как вейвлет, интеграл был бы нулем.
В шкалы, где колебание в вейвлете происходит на намного большей или меньшей шкале, чем период синусоиды, вы получаете коэффициенты CWT около нуля. Следующий рисунок иллюстрирует случай, когда вейвлет колеблется в гораздо меньшей шкале, чем синусоида.
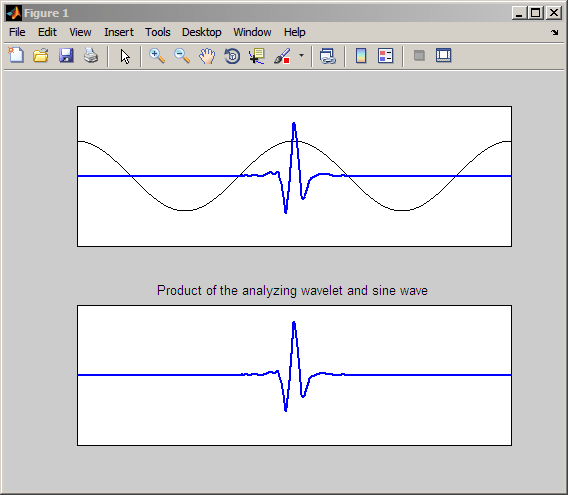
Продукт, показанный на нижней панели, тесно напоминает анализирующий вейвлет. Интеграция этого продукта приводит к коэффициенту CWT около нуля.
Следующий пример создает 60-Hz синусоиду и получает CWT с помощью sym8 вейвлет.
t = linspace(0,1,1000); x = cos(2*pi*60*t); CWTcoeffs = cwt(x,1:64,'sym8','plot'); colormap jet;
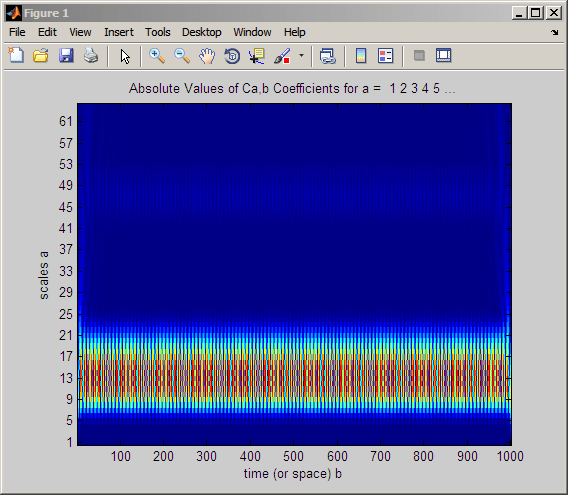
Обратите внимание, что коэффициенты CWT большие по абсолютному значению вокруг шкал с 9 по 21. Псевдочастоты, соответствующие этим шкалам, можно найти с помощью команды:
freq = scal2frq(9:21,'sym8',1/1000);
Обратите внимание, что коэффициенты CWT большие на шкалы около частоты синусоиды. Вы можете четко увидеть синусоидальный шаблон в коэффициентах CWT в этих шкалах со следующим кодом.
surf(CWTcoeffs); colormap jet;
shading('interp'); view(-60,12);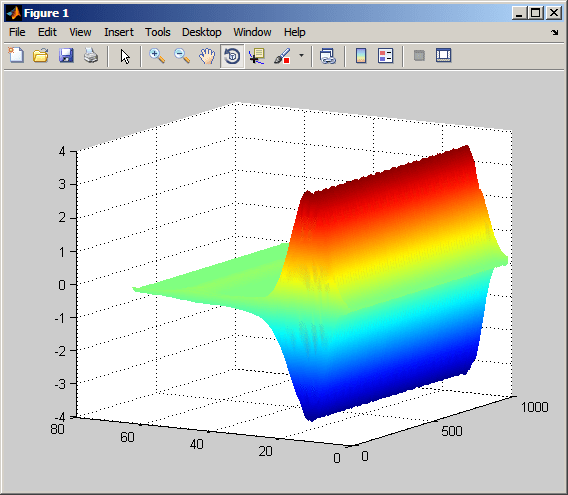
Конечный пример создает сигнал, состоящий как из резких переходов, так и из плавных колебаний. Сигнал является 2-Hz синусоидой с двумя введенными разрывами.
N = 1024;
t = linspace(0,1,1024);
x = 4*sin(4*pi*t);
x = x - sign(t - .3) - sign(.72 - t);
plot(t,x); xlabel('t'); ylabel('x');
grid on;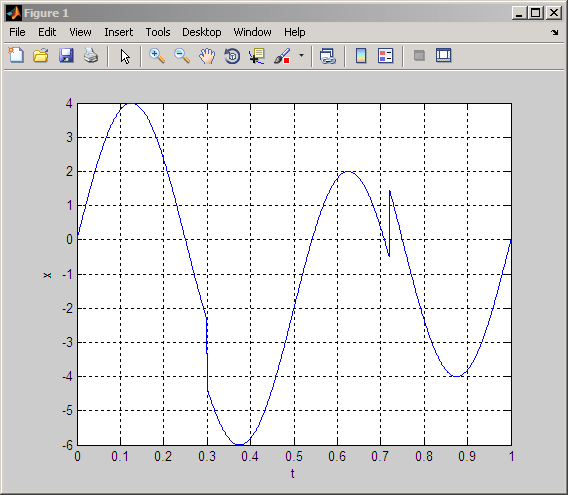
Обратите внимание на разрывы вблизи t = 0,3 и t = 0,7.
Получите и постройте график CWT с помощью sym4 вейвлет.
CWTcoeffs = cwt(x,1:180,'sym4');
imagesc(t,1:180,abs(CWTcoeffs));
colormap jet; axis xy;
xlabel('t'); ylabel('Scales');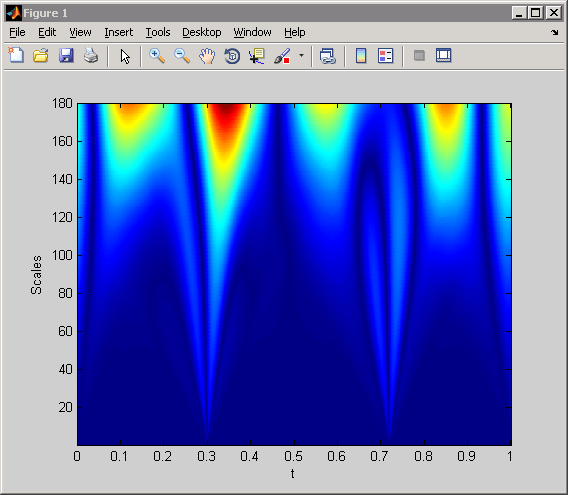
Обратите внимание, что CWT обнаруживает как резкие переходы, так и колебания в сигнале. Резкие переходы влияют на коэффициенты CWT во всех шкалах и четко отделяются от более плавных функций в малых шкалах. С другой стороны, максимумы и минимумы 2-Hz синусоиды заметны в коэффициентах CWT в больших шкалах и не видны в малых шкалах.
Следующие общие принципы важно иметь в виду при интерпретации коэффициентов CWT.
Конус влияния - В зависимости от шкалы, коэффициент CWT в точке может быть затронут значениями сигналов в точках, удаленных далеко. Необходимо учитывать поддержку вейвлета в определенных шкалах. Использоватьconofinf определить конус влияния. Не все вейвлеты равны в своей поддержке. Например, вейвлет Haar имеет меньшую поддержку во всех шкалах, чем sym4 вейвлет.
Обнаружение резких переходов - Вейвлеты очень полезны для обнаружения резких изменений в сигнале. Резкие изменения в сигнале производят относительно большие коэффициенты вейвлета (в абсолютном значении) с центром вокруг разрыва во всех шкалах. Из-за поддержки вейвлета набор коэффициентов CWT, на которые влияет особенность, увеличивается с увеличением шкалы. Напомним, это определение конуса влияния. Наиболее точная локализация разрыва на основе коэффициентов CWT получена в наименьших шкалах.
Обнаружение функций сглаживания сигнала - функции сглаживания сигнала генерируют относительно большие коэффициенты вейвлета в шкалах, где колебание в вейвлете лучше всего коррелирует с функцией сигнала. Для синусоидальных колебаний коэффициенты CWT отображают колебательный шаблон в шкалах, где колебание в вейвлете аппроксимирует период синусоиды .
Основной алгоритм непрерывного вейвлет (CWT):
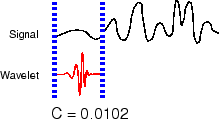
Возьмите вейвлет и сравните его с секцией в начале исходного сигнала.
Вычислим число, C, что представляет, насколько тесно коррелирован вейвлет с этой секцией сигнала. Чем больше число C в абсолютном значении, чем больше сходство. Это следует из того факта, что коэффициенты CWT вычисляются скалярным произведением. Смотрите Скалярные произведения для получения дополнительной информации о том, как скалярные произведения измеряют сходство. Если энергия сигнала и энергия вейвлета равны единице, C может быть интерпретирован как коэффициент корреляции. Обратите внимание, что в целом энергия сигнала не равна единице, и коэффициенты CWT не интерпретируются непосредственно как коэффициенты корреляции.
Как описано в Непрерывном и Дискретном Вейвлет Преобразовании, коэффициенты CWT явно зависят от анализирующего Вейвлета. Поэтому коэффициенты CWT различаются, когда вы вычисляете CWT для того же сигнала, используя различные вейвлеты.
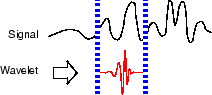
Сдвиньте вейвлет вправо и повторите шаги 1 и 2, пока вы не закроете весь сигнал.
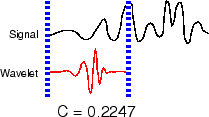
Масштабируйте (растягивайте) вейвлет и повторяйте шаги с 1 по 3.
Повторите шаги с 1 по 4 для всех шкал.