Daubechies вейвлета фильтрация расчета
The dbaux функция генерирует коэффициенты масштабирующего фильтра для вейвлетов «экстремальной фазы» Daubechies.
W = dbaux(N)N Масштабирующий фильтр Daubechies такой, что sum(W) = 1.
Примечание
Нестабильность может возникнуть, когда N слишком велик. Начиная со значений N в области значений 30-х годов выход функции больше не будет точно представлять коэффициенты масштабирующего фильтра.
Для N = 1, 2 и 3, порядок N Фильтры Symlet и упорядочивайте N Фильтры Daubechies идентичны. См. Экстремальная фаза.
Область расчета dbN Масштабирующий фильтр Daubechies требует извлечения корней полинома порядка 4N. Нестабильность может возникнуть, начиная со значений N в 30-е годы.
Используемый алгоритм основан на результате, полученном Shensa [3], показывающем соответствие между фильтрами «Lagrange а trous» и сверточными квадратами вейвлет Daubechies.
Расчет порядка <reservedrangesplaceholder2> масштабирующего фильтра Daubechies w протекает в два шага: вычислите P фильтра Lagrange, и извлеките квадратный корень. Точнее:
P связанный фильтр «Lagrange а trous» является симметричным фильтром 4N-1 длины. P определяется как
P = [a (<reservedrangesplaceholder7>) 0 <reservedrangesplaceholder6> (N-1) 0... 0 <reservedrangesplaceholder4> (1) 1 a (1) 0 <reservedrangesplaceholder2> (2) 0... 0 <reservedrangesplaceholder1> (<reservedrangesplaceholder0>)]
где
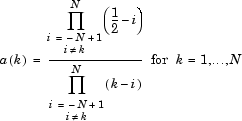
Затем, если w обозначает db N масштабирующий фильтр Daubechies из суммы![]() , w является квадратным корнем из P:
, w является квадратным корнем из P:
P = conv(wrev(w), w) где w является фильтром длины 2 N.
Соответствующий полином имеет N нули, расположенные в − 1, и N−1 нули менее 1 по модулю .
Обратите внимание, что могут использоваться другие методы; см. различные решения задачи спектрального факторизации в Strang-Nguyen [4] (стр. 157).
[1] Daubechies, I. Десять лекций по вейвлетам, серия региональных конференций CBMS-NSF по прикладной математике. Филадельфия, Пенсильвания: СИАМ Эд, 1992.
[2] Oppenheim, Alan V., and Ronald W. Schafer. Обработка сигнала в дискретном времени. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1989.
[3] Shensa, M.J. (1992), «The discrete wavelet transform: wedding the trous and Mallat Algorithms», IEEE Trans. on Signal Processing, vol. 40, 10, pp. 2464-2482.
[4] Strang, G., and T. Nguyen.Wavelets and Filter Banks. Wellesley, MA: Wellesley-Cambridge Press, 1996.