2-D вейвлет
[ возвращает вейвлет матрицы C,S] = wavedec2(X,N,wname)X на уровне N использование вейвлет- wname. Выход разложения состоит из вектора вейвлет C и матрицу бухгалтерии S, который содержит количество коэффициентов по уровню и ориентации.
Примечание
Для gpuArray входы, поддерживаемые режимы 'symh' ('sym') и 'per'. Если вход является gpuArray, дискретный режим расширения вейвлет, используемый в wavedec2 по умолчанию является 'symh' если текущий режим расширения не 'per'. Смотрите пример Многоуровневый 2 -D Дискретный Вейвлет преобразование на графическом процессоре.
Для изображений возможен алгоритм, подобный одномерному случаю, для двумерных вейвлетов и функций масштабирования, полученных из одномерных векторов тензорным продуктом. Этот вид двумерного DWT приводит к разложению коэффициентов аппроксимации на уровне j в четырёх компонентах: приближение на уровне j + 1 и детали в трех ориентациях (горизонтальной, вертикальной и диагональной).
График описывает основной шаг разложения для изображений:
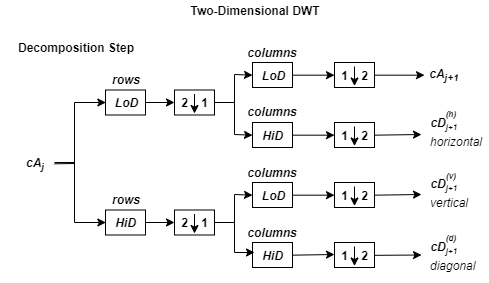
где
![]() - Downsample columns: сохраните четные индексированные столбцы.
- Downsample columns: сохраните четные индексированные столбцы.
![]() - Понижающие строки: сохраните четные индексированные строки.
- Понижающие строки: сохраните четные индексированные строки.
![]() - Свертка с фильтром X строки записи.
- Свертка с фильтром X строки записи.
![]() - Свертка с фильтром X столбцы записи.
- Свертка с фильтром X столбцы записи.
и
Инициализация: cA 0 = s.
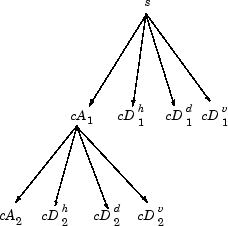
Таким образом, для J = 2 двумерное дерево вейвлет имеет вид
[1] Daubechies, Ингрид. Десять лекций по вейвлетам. Серия региональных конференций CBMS-NSF по прикладной математике 61. Филадельфия, Pa: Общество промышленной и прикладной математики, 1992.
[2] Mallat, S.G. «A Theory for Multirresolution Signal Decomposition: The Wavelet Representation». Транзакции IEEE по анализу шаблонов и машинной разведке 11, № 7 (июль 1989): 674-93. https://doi.org/10.1109/34.192463.
[3] Meyer, Y. Wavelets and Operators. Перевод Д. Х. Сэлинджера. Кембридж, Великобритания: Cambridge University Press, 1995.