dwt2
Одноуровневое дискретное 2-D вейвлет
Синтаксис
Описание
[ вычисляет одноуровневый 2-D DWT с режимом расширения cA,cH,cV,cD] = dwt2(___,'mode',extmode)extmode. Включите этот аргумент после всех других аргументов.
Примечание
Для gpuArray входы, поддерживаемые режимы 'symh' ('sym') и 'per'. Все 'mode' опции, кроме 'per' преобразуются в 'symh'. Смотрите пример Одноуровневый 2 -D Дискретный Вейвлет Преобразование на графическом процессоре.
Примеры
Одноуровневое 2-D дискретное вейвлет изображения
Загрузка и отображение изображения.
load woman
imagesc(X)
colormap(map)
Получите одноуровневое 2-D дискретное вейвлет изображения с помощью симлета порядка 4 и периодического расширения.
[cA,cH,cV,cD] = dwt2(X,'sym4','mode','per');
Отобразите вертикальные коэффициенты детализации и коэффициенты приближения.
imagesc(cV)
title('Vertical Detail Coefficients')
imagesc(cA)
title('Approximation Coefficients')
Одноуровневое 2-D дискретное преобразование Вейвлета с использованием фильтров
Загрузка и отображение изображения.
load sculpture imagesc(X) colormap gray
Сгенерируйте lowpass и highpass фильтры разложения для вейвлета Haar.
[LoD,HiD] = wfilters('haar','d');
Используйте фильтры для выполнения одноуровневого 2-D вейвлет. Используйте симметричное расширение с полуточкой. Отобразите приближения и детализации.
[cA,cH,cV,cD] = dwt2(X,LoD,HiD,'mode','symh'); subplot(2,2,1) imagesc(cA) colormap gray title('Approximation') subplot(2,2,2) imagesc(cH) colormap gray title('Horizontal') subplot(2,2,3) imagesc(cV) colormap gray title('Vertical') subplot(2,2,4) imagesc(cD) colormap gray title('Diagonal')
Одноуровневый 2 -D дискретный Вейвлет преобразование на графическом процессоре
Обратитесь к разделу Поддержка GPU по версии (Parallel Computing Toolbox), чтобы узнать, какие графические процессоры поддерживаются.
Загрузка изображения. Поместите изображение на графический процессор с помощью gpuArray. Сохраните текущий режим расширения.
load mask imgg = gpuArray(X); origMode = dwtmode('status','nodisp');
Использование dwtmode для изменения режима внутреннего абонента на нулевое заполнение. Получите одноуровневый 2-D DWT изображения на графическом процессоре с помощью db2 вейвлет.
dwtmode('zpd','nodisp') [cA,cH,cV,cD] = dwt2(imgg,'db2');
Текущий режим расширения zpd не поддерживается для gpuArray вход. Поэтому DWT выполняется вместо этого с помощью sym режим расширения. Подтвердите это, взяв DWT imgg с установленным на sym режимом расширения и сравните с предыдущим результатом.
[cAsym,cHsym,cVsym,cDsym] = dwt2(imgg,'db2','mode','sym'); [max(abs(cA(:)-cAsym(:))) max(abs(cH(:)-cHsym(:))) ... max(abs(cV(:)-cVsym(:))) max(abs(cD(:)-cDsym(:)))]
ans =
0 0 0 0
Неподдерживаемый режим расширения, заданный в качестве входного параметра, преобразуется в 'sym'. Подтвердите, что взятие DWT imgg с 'mode' set в неподдерживаемом режиме также по умолчанию задает значение sym режим расширения.
[cA,cH,cV,cD] = dwt2(imgg,'db2','mode','spd'); [max(abs(cA(:)-cAsym(:))) max(abs(cH(:)-cHsym(:))) ... max(abs(cV(:)-cVsym(:))) max(abs(cD(:)-cDsym(:)))]
ans =
0 0 0 0
Измените текущий режим внутреннего абонента на периодический. Получите одноуровневый DWT изображения на графическом процессоре с помощью db2 вейвлет.
dwtmode('per','nodisp') [cA,cH,cV,cD] = dwt2(imgg,'db2');
Подтвердите текущий режим расширения per поддерживается для gpuArray вход.
[cAper,cHper,cVper,cDper] = dwt2(imgg,'db2','mode','per'); [max(abs(cA(:)-cAper(:))) max(abs(cH(:)-cHper(:))) ... max(abs(cV(:)-cVper(:))) max(abs(cD(:)-cDper(:)))]
ans =
0 0 0 0
Восстановите режим расширения к исходной настройке.
dwtmode(origMode,'nodisp')Входные параметры
Выходные аргументы
Алгоритмы
Алгоритм 2-D вейвлетов разложения для изображений похож на одномерный случай. Двумерные функции вейвлета и масштабирования получаются путем взятия тензорных продуктов одномерных функций вейвлета и масштабирования. Этот вид двумерного DWT приводит к разложению коэффициентов аппроксимации на уровне j в четырёх компонентах: приближение на уровне j + 1 и детали в трех ориентациях (горизонтальной, вертикальной и диагональной). Следующий график описывает основные шаги разложения для изображений.
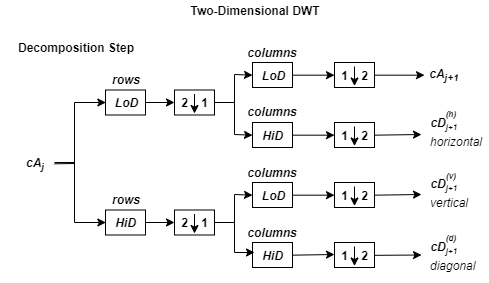
где
- Понижающий отсчет столбцов: сохраните четные индексированные столбцы
- Понижающие строки: сохраните четные индексированные строки
- Свернуть с фильтром X строки записи
- Свертка с фильтром X столбцов записи
Разложение инициализируется путем установки коэффициентов приближений, равных s изображения: cA 0 = s.
Примечание
Чтобы справиться с эффектами конца сигнала, введенными основанным на свертке алгоритмом, 1-D и 2-D DWT используют глобальную переменную, управляемую dwtmode. Эта переменная определяет тип используемого режима расширения сигнала. Возможные опции включают заполнение нулями и симметричное расширение, которое является режимом по умолчанию.
Ссылки
[1] Daubechies, Ингрид. Десять лекций по вейвлетам. Серия региональных конференций CBMS-NSF по прикладной математике 61. Филадельфия, Pa: Общество промышленной и прикладной математики, 1992.
[2] Mallat, S.G. «A Theory for Multirresolution Signal Decomposition: The Wavelet Representation». Транзакции IEEE по анализу шаблонов и машинной разведке 11, № 7 (июль 1989): 674-93. https://doi.org/10.1109/34.192463.
[3] Meyer, Y. Wavelets and Operators. Перевод Д. Х. Сэлинджера. Кембридж, Великобритания: Cambridge University Press, 1995.