Метод подъема для построения вейвлетов

Так называемые вейвлеты первой генерации и функции масштабирования являются диадическими расширениями и переводами одной функции. Методы Фурье играют ключевую роль в проекте этих вейвлеты. Однако требование, чтобы вейвлет базиса состоял из переводов и расширений одной функции, накладывает некоторые ограничения, которые ограничивают утилиту мультиразрешения идеи в основе вейвлета анализа.

Утилита вейвлет-методов расширяется за счет проекта вейвлеты второй генерации посредством подъема.

Типичные настройки, где перевод и расширение одной функции не могут использоваться, включают:

Разработка вейвлетов на ограниченных областях - это включает конструкцию вейвлетов на интервале или ограниченной области в высокомерном евклидовом пространстве.
Взвешенные вейвлеты - В некоторых приложениях, таких как решение дифференциальных уравнений с частными производными, требуются вейвлеты биортогональные относительно взвешенного скалярного произведения.
Нерегулярно разнесенные данные - Во многих реальных приложениях интервал дискретизации между выборками данных не равен.

Разработка новых вейвлеты первой генерации требует экспертизы в анализе Фурье. Метод подъема, предложенный Sweldens (см. [Swe98] в ссылки), устраняет необходимость экспертизы в анализе Фурье и позволяет вам сгенерировать бесконечное число дискретных биортогональных вейвлеты, начиная с начального. В дополнение к генерации вейвлетов первого поколения с подъемом, метод подъема также позволяет вам проектировать вейвлеты второго поколения, которые не могут быть разработаны с помощью методов, основанных на Фурье. С помощью лифтинга можно проектировать вейвлеты, которые устраняют недостатки вейвлетов первой генерации.

Для получения дополнительной информации о подъеме см. [Swe98], [Mal98], [StrN96] и [MisMOP03] в ссылках.

Фон подъема

Открыть Live Script

DWT, реализованный набором фильтров, определяется четырьмя фильтрами, как описано в Алгоритме быстрого Преобразования Вейвлет (FWT). Два основных свойства интереса:

Идеальное свойство реконструкции
Ссылка с «истинными» вейвлетами (как сгенерировать, начиная с фильтров, ортогональные или биортогональные основания пространства функций конечной энергии)

Чтобы проиллюстрировать идеальное свойство реконструкции, следующая группа фильтров содержит два фильтра разложения и два фильтра синтеза. Фильтры разложения и синтеза могут составлять пару биортогональных основ или ортогональный базис. Заглавные буквы обозначают Z-преобразования фильтров.

Это приводит к следующим двум условиям для идеальной реконструкции (PR) банка фильтров:

$H_{}^{\sim} (z) H (z) + G_{}^{\sim} (z) G (z) = 2 z^{- L + 1}$

$H_{}^{\sim} (- z) H (z) + G_{}^{\sim} (- z) G (z) = 0$

Первое условие обычно (неправильно) называется идеальным условием реконструкции, а второе - условием сглаживания.

$z^{- L + 1}$ термин подразумевает, что совершенная реконструкция достигается до задержки на один образец меньше, чем длина фильтра, L. Это приводит, если фильтры анализа сдвинуты, чтобы быть причинными.

Лифтинг проектирует идеальные восстановительные фильтрующие банки, начиная с основной природы вейвлет. Вейвлет строят разреженные представления, используя корреляцию, присущую большинству данных реального мира. Например, постройте пример потребления электроэнергии в течение 3-дневного периода.

load leleccum
plot(leleccum)
grid on
axis tight
title('Electricity Consumption')

Figure contains an axes. The axes with title Electricity Consumption contains an object of type line.

Представление полифазы

Полифазное представление сигнала является важной концепцией в подъёме. Можно рассматривать каждый сигнал как состоящий из фаз, которые состоят из взятия каждой N -й выборки, начиная с некоторого индекса. Для примера, если вы индексируете временные ряды от n = 0 и берете каждую другую выборку, начиная с n = 0, вы извлекаете четные выборки. Если вы берете каждую другую выборку, начиная с n = 1, вы извлекаете нечетные выборки. Это четные и нечетные полифазные компоненты данных. Поскольку ваш шаг между выборками равен 2, существует только две фазы. Если вы увеличили шаг до 4, можно извлечь 4 фазы. Для подъема достаточно сконцентрироваться на четных и нечетных полифазных компонентах. Следующая схема иллюстрирует эту операцию для входного сигнала.

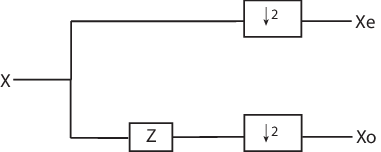
где Z обозначает оператор опережающего модуля, а стрела вниз с числом 2 представляет собой понижающую дискретизацию на две. На языке подъема операция разделения входного сигнала на четные и нечетные компоненты известна как операция разделения или ленивый вейвлет.

Чтобы понять лифтинг математически, необходимо понять представление z-области четных и нечетных полифазных компонентов.

Z-преобразование четного полифазного компонента

$X_{0} (z) = \sum_{n} x (2 n) z^{- n}$

Z-преобразование нечетного полифазного компонента

$X_{1} (z) = \sum_{n} x (2 n + 1) z^{- n}$

Можно записать z-преобразование входного сигнала как сумму расширенных версий z-преобразований полифазных компонентов.

$X (z) = \sum_{n} x (2 n) z^{- 2 n} + \sum_{n} x (2 n + 1) z^{- 2 n + 1} = X_{0} (z^{2}) + z^{- 1} X_{1} (z^{2})$

Разделение, предсказание и обновление

Один этап подъема может быть описан следующими тремя основными операциями:

Разделение - сигнал на несвязанные компоненты. Общим способом сделать это является извлечение четных и нечетных полифазных компонентов, объясненных в Polyphase Representation. Это также известно как ленивый вейвлет.
Предсказать - нечетный полифазный компонент, основанный на линейной комбинации выборок четного полифазного компонента. Выборки нечетного полифазного компонента заменяются различием между нечетным полифазным компонентом и предсказанным значением.
Обновление - четный полифазный компонент, основанный на линейной комбинации различий выборок, полученных на этапе предсказания.

На практике нормализация включена как для операций прогнозирования, так и для операций обновления.

Следующая схема иллюстрирует один шаг подъема.

Haar Wavelet через лифтинг

Открыть Live Script

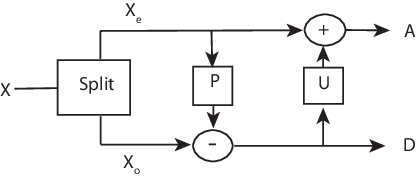
Используя операции в Split, Predict и Update, можно реализовать вейвлет Haar через подъем.

Разделение - Разделите сигнал на четные и нечетные полифазные компоненты
Предсказать - Заменить $x (2 n + 1)$ с $d (n) = x (2 n + 1) - x (2 n)$ . Оператор предсказания просто $x (2 n)$ .
Обновление - Замена $x (2 n)$ с $x (2 n) + d (n) / 2$ . Это равно $(x (2 n) + x (2 n + 1)) / 2$ .

Оператор предсказания в Z-области может быть записан в следующей матричной форме:

$[\begin{array}{c} 1 & 0 \\ - P (z) & 1 \end{array}] [\begin{array}{c} X_{0} (z) \\ X_{1} (z) \end{array}]$

с $P (z) = 1$ .

Оператор обновления может быть записан в следующей матричной форме:

$[\begin{array}{c} 1 & S (z) \\ 0 & 1 \end{array}] [\begin{array}{c} 1 & 0 \\ - P (z) & 1 \end{array}] [\begin{array}{c} X_{0} (z) \\ X_{1} (z) \end{array}]$

с $S (z) = 1 / 2$ .

Наконец, обновление и прогнозирование нормализации могут быть включены следующим образом:

$[\begin{array}{c} \sqrt{2} & 0 \\ 0 & \frac{1}{\sqrt{2}} \end{array}] [\begin{array}{c} 1 & S (z) \\ 0 & 1 \end{array}] [\begin{array}{c} 1 & 0 \\ - P (z) & 1 \end{array}] [\begin{array}{c} X_{0} (z) \\ X_{1} (z) \end{array}]$

Можно использовать liftingScheme чтобы создать схему подъема, связанную с вейвлет Haar.

lscHaar = liftingScheme('Wavelet','haar');
disp(lscHaar)

 	 Wavelet              : 'haar' 
 	 LiftingSteps         : [2 × 1] liftingStep 
 	 NormalizationFactors : [1.4142 0.7071] 
 	 CustomLowpassFilter  : [] 


 Details of LiftingSteps :
            Type: 'predict'
    Coefficients: -1
        MaxOrder: 0

            Type: 'update'
    Coefficients: 0.5000
        MaxOrder: 0

Обратите внимание, что для удобства отрицательный знак включен в predict этап подъема. Элементы NormalizationFactors, 1.4142 и 0.7071, являются факторами нормализации прогноза и обновления, соответственно. MaxOrder приводит наивысшую степень полинома Лорана, которая описывает соответствующий шаг подъема. В этом случае оба являются нулем, потому что прогнозирующие и обновляющие лифты оба описаны скалярами.

Bior2.2 вейвлет через подъем

Открыть Live Script

Этот пример представляет схему подъема для bior2.2 биортогональное масштабирование и вейвлет.

В схеме подъема Haar оператор предсказания дифференцировал нечетные и четные выборки. В этом примере задайте новый оператор предсказания, который вычисляет среднее значение двух соседних четных выборок. Вычесть среднее значение из промежуточной нечетной выборки.

$d (n) = x (2 n + 1) - \frac{1}{2} [x (2 n) + x (2 n + 2)]$

В Z-домене можно записать оператор предсказания как

$[\begin{array}{c} 1 & 0 \\ - \frac{1}{2} (1 - z) & 1 \end{array}] [\begin{array}{c} X_{0} (z) \\ X_{1} (z) \end{array}]$

Для получения оператора обновления исследуйте оператор обновления в Haar Wavelet Via Lifting. Обновление задано таким образом, что сумма коэффициентов приближения пропорциональна среднему значению вектора входных данных.

$\sum_{n} x (n) = \frac{1}{2} \sum_{n} a (n)$

Чтобы получить тот же результат на этом шаге подъема, задайте обновление как

$[\begin{array}{c} 1 & \frac{1}{4} (z^{- 1} + 1) \\ 0 & 1 \end{array}] [\begin{array}{c} 1 & 0 \\ - \frac{1}{2} (1 + z) & 1 \end{array}] [\begin{array}{c} X_{0} (z) \\ X_{1} (z) \end{array}]$

Можно использовать liftingScheme для получения схемы подъема.

lscBior = liftingScheme('Wavelet','bior2.2');
disp(lscBior)

 	 Wavelet              : 'bior2.2' 
 	 LiftingSteps         : [2 × 1] liftingStep 
 	 NormalizationFactors : [1.4142 0.7071] 
 	 CustomLowpassFilter  : [] 


 Details of LiftingSteps :
            Type: 'predict'
    Coefficients: [-0.5000 -0.5000]
        MaxOrder: 1

            Type: 'update'
    Coefficients: [0.2500 0.2500]
        MaxOrder: 0

Добавьте шаг подъема к схеме подъема Haar

Открыть Live Script

В этом примере показано, как добавить элементарный шаг подъема к схеме подъема.

Создайте схему подъема, связанную с вейвлетом Haar.

lsc = liftingScheme('Wavelet','haar');
disp(lsc)

 	 Wavelet              : 'haar' 
 	 LiftingSteps         : [2 × 1] liftingStep 
 	 NormalizationFactors : [1.4142 0.7071] 
 	 CustomLowpassFilter  : [] 


 Details of LiftingSteps :
            Type: 'predict'
    Coefficients: -1
        MaxOrder: 0

            Type: 'update'
    Coefficients: 0.5000
        MaxOrder: 0

Создайте update этап элементарного подъема. Добавьте шаг к схеме подъема.

els = liftingStep('Type','update','Coefficients',[-1/8 1/8],'MaxOrder',0);
lscNew = addlift(lsc,els);
disp(lscNew)

 	 Wavelet              : 'custom' 
 	 LiftingSteps         : [3 × 1] liftingStep 
 	 NormalizationFactors : [1.4142 0.7071] 
 	 CustomLowpassFilter  : [] 


 Details of LiftingSteps :
            Type: 'predict'
    Coefficients: -1
        MaxOrder: 0

            Type: 'update'
    Coefficients: 0.5000
        MaxOrder: 0

            Type: 'update'
    Coefficients: [-0.1250 0.1250]
        MaxOrder: 0

Получите фильтры разложения и реконструкции из новой схемы подъема.

[lod,hid,lor,hir] = ls2filt(lscNew);

Использование bswfun для построения графика полученной функции масштабирования и фильтра.

bswfun(lod,hid,lor,hir,'plot');

Figure contains 4 axes. Axes 1 with title Analysis scaling function (phiA) contains an object of type line. Axes 2 with title Analysis wavelet function (psiA) contains an object of type line. Axes 3 with title Synthesis scaling function (phiS) contains an object of type line. Axes 4 with title Synthesis wavelet function (psiS) contains an object of type line.

Целочисленное целочисленное преобразование вейвлета

Открыть Live Script

В нескольких приложениях желательно иметь вейвлет преобразование, которое преобразует целое число входов в целочисленные коэффициенты масштабирования и вейвлета. Вы можете выполнить легко используя лифтинг.

Создайте схему подъема, связанную с вейвлетом Haar. Добавьте элементарный шаг подъема к схеме подъема.

lsc = liftingScheme('Wavelet','haar');
els = liftingStep('Type','update','Coefficients',[-1/8 1/8],'MaxOrder',0);
lscNew = lsc.addlift(els);

Создайте целочисленный сигнал. Получите целочисленное вейвлет сигнала от LWT, используя схему подъема, с 'Int2Int' установлено на true.

rng default
sig = randi(20,16,1);
[ca,cd] = lwt(sig,'LiftingScheme',lscNew,'Int2Int',true);

Подтвердите, что коэффициенты приближения все целые числа.

max(abs(ca-floor(ca)))

ans = 0

Подтвердите, что коэффициенты детализации все целые числа.

len = length(cd);
for k=1:len
    disp([k, max(abs(cd{k}-floor(cd{k})))]);
end

Инвертируйте преобразование и демонстрируйте идеальную реконструкцию.

xrec = ilwt(ca,cd,'LiftingScheme',lscNew,'Int2Int',true);
max(abs(xrec-sig))

ans = 0

Документация