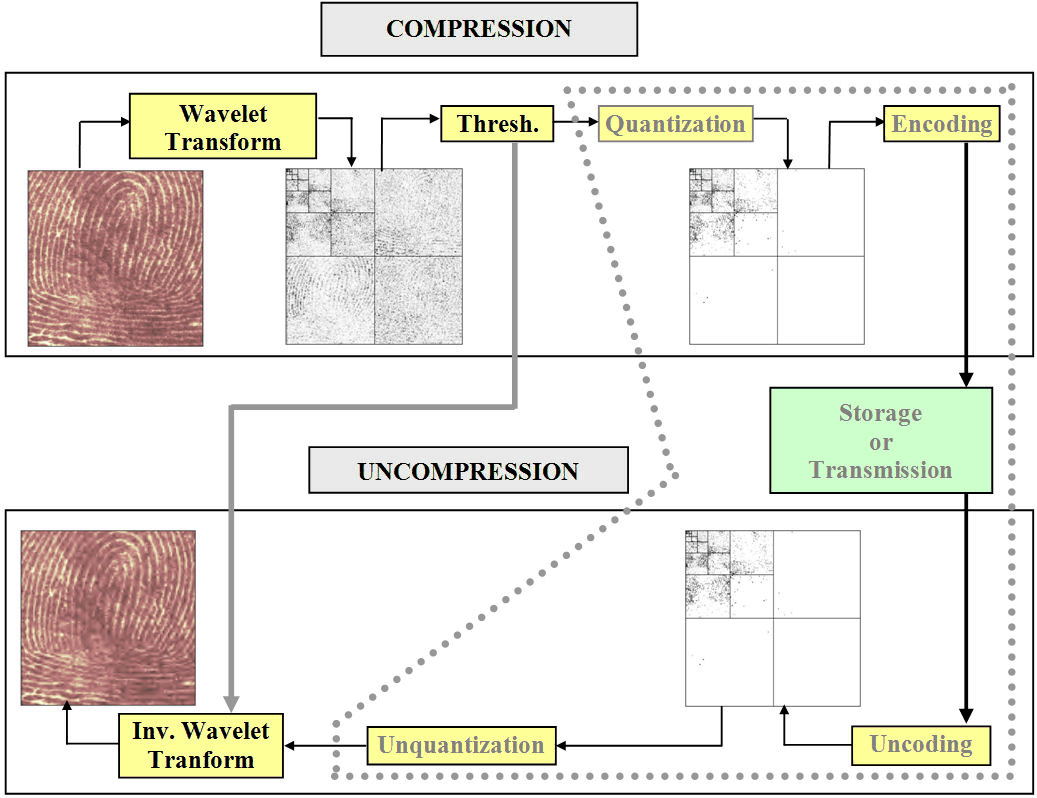
В Wavelet Data Compression мы рассмотрели аспекты, конкретно связанные со сжатием с помощью вейвлетов. Однако в сложение с алгоритмами, связанными с вейвлетами, такими как DWT и IDWT, необходимо использовать другие ингредиенты, относящиеся к режиму квантования и типу кодирования в порядок с истинным сжатием.
Этот более сложный процесс может быть представлен следующим рисунком.
Покажем эффекты квантования на визуализации изображения отпечатка пальца. Это индексированное изображение соответствует матрице целых чисел в диапазоне от 0 до 255. Посредством квантования мы можем уменьшить количество цветов, которое здесь равно 256.
Следующий рисунок иллюстрирует, как уменьшить с 256 до 16 цветов путем работы со значениями оригинального изображения.
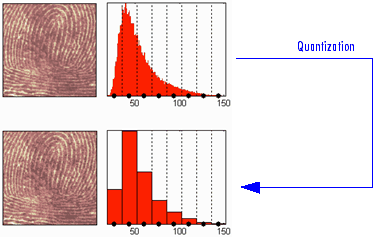
Мы видим на этом рисунке:
В верхней части
Слева: оригинальное изображение
Справа: соответствующая гистограмма значений
Внизу
Слева: реконструированное изображение
Справа: соответствующая гистограмма квантованных значений
Это квантование приводит к сжатию изображения. Действительно, с двоичным кодом фиксированной длины необходимо 8 бит на пиксель, чтобы кодировать 256 цветов и 4 бита на пиксель, чтобы кодировать 16 цветов. Мы замечаем, что изображение, полученное после квантования, имеет хорошее качество. Однако в среду истинного сжатия квантование используется не на оригинальное изображение, а на его вейвлет разложении.
Давайте разложим изображение отпечатка пальца на уровне 4 с помощью вейвлета Haar. Гистограмма вейвлет-коэффициентов и квантованная гистограмма нормированы так, что значения варьируются между -1 и + 1. 15 интервалов квантования не имеют одинаковой длины.
Следующий рисунок иллюстрирует, как уменьшить информацию путем раскладывания на значениях коэффициентов вейвлета оригинального изображения.
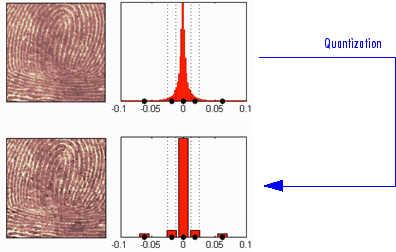
Мы видим на этом рисунке:
В верхней части
Слева: оригинальное изображение
Справа: соответствующая гистограмма (центральная часть) значений коэффициентов
Внизу
Слева: реконструированное изображение
Справа: соответствующая гистограмма (центральная часть) квантованных значений коэффициентов
Ключевой точкой является то, что гистограмма квантованных коэффициентов массово концентрируется в классе с центром в 0. Отметим, что еще раз полученное изображение хорошего качества.
Основные идеи, представленные выше, используются тремя методами, которые каскадируют за один шаг, пороговое значение коэффициента (глобальное или по уровню) и кодирование квантованием. Фиксированное или кодирование Хаффмана может использоваться для квантования в зависимости от метода.
В следующей таблице представлены эти методы, часто называемые методами порогового удержания коэффициентов (CTM), и дается MATLAB® имя, используемое истинными инструментами сжатия для каждого из них.
Имя MATLAB | Имя метода сжатия |
|---|---|
'gbl_mmc_f' | Глобальное пороговое значение коэффициентов и фиксированное кодирование |
'gbl_mmc_h' | Глобальное пороговое значение коэффициентов и кодирование Хаффмана |
'lvl_mmc' | Поддиапазонное пороговое значение коэффициентов и кодирование Хаффмана |
Доступны более сложные методы, которые объединяют вейвлет разложение и квантование. Это основной принцип прогрессивных методов.
С одной стороны, прогрессивность делает возможным во время декодирования получить изображение, разрешение которого увеличивается постепенно. В сложение возможно получить набор коэффициентов сжатия на основе длины сохраненного кода. Это сжатие обычно приводит к потере информации, но этот вид алгоритма включает также сжатие без потерь.
Такие методы основаны на трех идеях. Двумя первыми, уже упомянутыми, являются использование вейвлет для обеспечения разреженности (большое количество нулевых коэффициентов) и классические методы кодирования. Третья идея, решающая для использования вейвлетов при сжатии изображений, заключается в том, чтобы в корне использовать древовидную структуру вейвлет-разложения. Некоторые коды, разработанные с 1993 по 2000 год, используют эту идею, в частности, алгоритм кодирования EZW, введённый Шапиро. См. раздел [Sha93] в ссылках».
EZW объединяет пошаговое пороговое и прогрессивное квантование, фокусируясь на более эффективном способе кодирования коэффициентов изображения, порядка минимизировать степень сжатия. Два варианта SPIHT и STW (см. следующую таблицу) являются уточненными версиями семенного алгоритма EZW.
Следуя несколько другой цели, WDR (и ASWDR уточнения) фокусируется на том, что в целом некоторые фрагменты данного изображения требуют более точного кодирования, что приводит к лучшему восприятию результата, даже если обычно существует небольшая цена для оплаты с точки зрения степени сжатия.
Полный обзор этих прогрессивных методов приведен в ссылке Walker [Wal99] в ссылки.
Следующая таблица суммирует эти методы, часто называемые Прогрессивными Методами Значимости Коэффициентов (PCSM), и дает кодированное имя MATLAB, используемое истинными инструментами сжатия для каждого из них.
Имя MATLAB | Имя метода сжатия |
|---|---|
'ezw' | Встраиваемый Zerotree Wavelet |
'spiht' | Установите секционирование в иерархических деревьях |
'stw' | Древовидный вейвлет пространственной ориентации |
'wdr' | Уменьшение различия вейвлетов |
'aswdr' | Адаптивно сканированное уменьшение различия вейвлет |
'spiht_3d' | Установите разбиение на иерархические деревья 3D для изображений truecolor |
Следующие количественные измерения и показатели перцептивного качества полезны для анализа вейвлет и изображений.
M S E - Средняя квадратная ошибка (MSE) является квадратной нормой различия между данными и приближением сигнала или изображения, разделенным на количество элементов. MSE определяется:
Max Error - Максимальная ошибка - это максимальное абсолютное квадратное отклонение в приближении сигнала или изображения.
L2-Norm Ratio - L2-norm отношение является отношением квадратов L2-norm сигнала или приближения изображения к входному сигналу или изображению. Для изображений изображение изменяется как вектор-столбец перед принятием L2-norm
P S N R - отношение пикового сигнала к шуму (PSNR) является мерой пиковой ошибки в децибелах. PSNR имеет значение только для данных, закодированных с точки зрения бит на выборку или биты на пиксель. Чем выше PSNR, тем лучше качество сжатого или восстановленного изображения. Типичные значения для сжатия изображения с потерями составляют от 30 до 50 дБ. Когда PSNR больше 40 дБ, тогда эти два изображения неразличимы. PSNR определяется:
B P P - Биты на пиксель (BPP) - количество бит, требуемых для хранения одного пикселя изображения. BPP является степенью сжатия, умноженной на 8, принимая один байт на пиксель (8 биты).
Comp Ratio - Коэффициент сжатия - это отношение количества элементов в сжатом изображении, разделенное на количество элементов в оригинальное изображение, выраженное в процентах.
Можно найти примеры, иллюстрирующие режим командной строки и инструменты приложения для истинного сжатия в Wavelet Compression for Images и странице с описанием для wcompress.
Более подробная информация об истинном сжатии для изображений и более точно о способах сжатия содержится в [Wal99], [Sha93], [Sai96], [StrN96] и [Chr06]. См. Ссылки.