Что такое Прогнозирующее Управление Модели?

Прогнозирующее управление модели (MPC) является методом оптимального управления, в котором расчетные действия управления минимизируют функцию стоимости для ограниченной динамической системы по конечному, возвращению захваченного, горизонту.

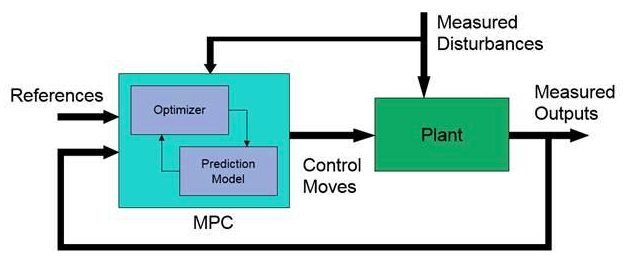
На каждом временном шаге контроллер MPC получает или оценивает текущее состояние объекта. Это затем вычисляет последовательность действий управления, которая минимизирует стоимость по горизонту путем решения ограниченной задачи оптимизации, которая использует внутреннюю модель объекта управления и зависит от состояния существующей системы. Контроллер затем обращается к объекту только первое вычисленное действие управления, игнорируя следующие единицы. В следующем временном шаге повторения процесса.

MPC основной цикл управления

Feedback loop with an MPC controller (consisting of an optimizer and a prediction model) connected to a plant. The controller receives a reference signal and the plant output, and outputs plant control moves.

Когда функция стоимости квадратична, объект линеен и без ограничений, и горизонт стремится к бесконечности, MPC эквивалентен управлению линейно-квадратичного регулятора (LQR) или управлению линейно-квадратичным гауссовым (LQG), если Фильтр Калмана оценивает состояние объекта от своих вводов и выводов.

На практике, несмотря на конечный горизонт, MPC часто наследовал много полезных характеристик традиционного оптимального управления, таких как способность естественно обработать объекты мультивхода мультивыводится (MIMO), возможность контакта с задержками (возможно различной длительности в различных каналах), и встроенные свойства робастности против моделирования ошибок. Номинальная устойчивость может также быть гарантирована при помощи определенных терминальных ограничений. Другими дополнительными важными функциями MPC является его способность явным образом обработать ограничения и возможность использования информации о будущей ссылке и сигналах воздействия, когда доступно.

Решение ограниченного оптимального управления онлайн на каждом временном шаге может потребовать существенных вычислительных ресурсов. Однако в некоторых случаях, такой что касается линейных ограниченных объектов, можно предварительно вычислить и сохранить закон о надзоре через целое пространство состояний, а не решить оптимизацию в режиме реального времени. Этот подход известен как явный MPC.

Рабочий процесс проекта MPC

В самом простом случае (также известный как традиционный, или линейный, MPC), в котором и объект и ограничения линейны и функция стоимости квадратична, общий рабочий процесс, чтобы разработать контроллер MPC включает следующие шаги.

MPC design workflow with 7 steps: Specify Plant, Define Signal Type, Create MPC Object, Simulate Closed Loop, Refine Design, Speed up Execution, and Deploy Controller

  1. Укажите, что объект — Задает внутреннюю модель объекта управления что контроллер MPC использование, чтобы предсказать поведение объекта через горизонт предсказания. Как правило, вы получаете эту модель объекта управления путем линеаризации нелинейного объекта в данной рабочей точке и определения его как объекта LTI, такой как ss, tf, и zpk. Можно также идентифицировать объект с помощью программного обеспечения System Identification Toolbox™. Обратите внимание на то, что одно ограничение - то, что объект не может иметь прямого сквозного соединения между своим входом управления и любым выходом. Для получения дополнительной информации об этом шаге смотрите Построение Линейные Независимые от времени Модели, Задайте Мультивход Мультивыходные Объекты, Линеаризуйте Модели Simulink, Линеаризуйте Модели Simulink Используя MPC Designer и Идентифицируйте Объект из Данных.

  2. Задайте типы сигнала — В целях проекта MPC, сигналы объекта обычно категоризируются в различные типы ввода и вывода. Вы обычно используете setmpcsignals задавать, в объекте объекта, заданном на предыдущем шаге, измеряется ли каждый объект выход или не измерен, и является ли каждый вход объекта переменной, которой управляют (то есть, вход управления) или измеренное или неизмеренное воздействие. В качестве альтернативы можно задать типы сигнала в MPC Designer. Для получения дополнительной информации смотрите Типы Сигнала MPC.

  3. Создайте объект MPC — После определения типов сигнала в объекте объекта, вы создаете mpc объект в MATLAB® рабочая область (или в MPC Designer), и задает, в объекте, параметры контроллера, такие как шаг расчета, предсказание и управляет горизонтами, весами функции стоимости, ограничениями и возмущениями. Следующее является обзором самых важных параметров, которые необходимо выбрать.

    1. Шаг расчета — типичное начальное приближение состоит из установки шага расчета контроллера так, чтобы 10 - 20 выборок могли покрыть желаемое время нарастания системы.

    2. Горизонт предсказания — количество будущих выборок, по которым диспетчер пытается минимизировать стоимость. Это должно быть достаточно длинно, чтобы получить переходный процесс и покрыть значительную динамику системы. Более длинный горизонт увеличивает и эффективность и вычислительные требования. Типичный горизонт предсказания является 10 - 20 выборками.

    3. Управляйте горизонтом — количество свободных перемещений управления что использование контроллера, чтобы минимизировать стоимость по горизонту предсказания. Так же к горизонту предсказания, более длинный горизонт управления увеличивает и эффективность и вычислительные требования. Хорошее эмпирическое правило для горизонта управления должно установить его от 10% до 20% горизонта предсказания при наличии минимума двух - трех шагов. Для получения дополнительной информации о шаге расчета и горизонте, смотрите, Выбирают Sample Time и Horizons.

    4. Номинальная стоимость — Если ваш объект выведен из линеаризации нелинейной модели вокруг рабочей точки, хорошая практика, должна установить номинальные значения для входа, состояния, утвердить производную (если ненулевой), и вывести. Выполнение так позволяет вам задавать ограничения на фактические вводы и выводы (вместо того, чтобы делать так на отклонениях от их номинальной стоимости) и позволяет вам симулировать замкнутый цикл и визуализировать сигналы более легко при использовании Simulink® или sim команда.

    5. Масштабные коэффициенты — Хорошая практика должна задать масштабные коэффициенты для каждого ввода и вывода объекта, особенно когда их область значений и величина очень отличаются. Соответствующие масштабные коэффициенты улучшают числовое условие базовой задачи оптимизации и делают вес, настраивающийся легче. Хорошая рекомендация состоит в том, чтобы установить масштабный коэффициент, приблизительно равняются промежутку (различие между максимальным и минимальным значением в технических модулях) связанного сигнала. Для получения дополнительной информации смотрите, Задают Масштабные коэффициенты.

    6. Ограничения — Ограничения обычно отражают физические пределы. Можно задать ограничения как любой трудно (не может быть нарушен в оптимизации), или мягкий (может быть нарушен до маленькой степени). Хорошая рекомендация состоит в том, чтобы установить трудные ограничения, при необходимости, на входных параметрах или их скорости изменения, в то время как установка выходные ограничения, при необходимости, как мягкие. Установка трудных ограничений и на вход и на выходные параметры может привести к недопустимости и в целом не рекомендуется. Для получения дополнительной информации смотрите, Задают Ограничения.

    7. Веса — можно приоритизировать цели эффективности контроллера путем корректировки настраивающих весов функции стоимости. Как правило, большие выходные веса обеспечивают агрессивную эффективность отслеживания уставки, в то время как большие веса на плавающих курсах, которыми управляют, способствуют более сглаженным перемещениям управления, которые улучшают робастность. Для получения дополнительной информации смотрите Веса Мелодии.

    8. Воздействие и шумовые модели — внутренняя модель предсказания, что использование контроллера, чтобы вычислить действие управления обычно состоит из модели объекта управления, увеличенной с моделями для воздействий и шума измерения влияние на объект. Возмущения задают динамические характеристики неизмеренных воздействий на вводах и выводах, соответственно, таким образом, они могут быть лучше отклонены. По умолчанию эти возмущения приняты, чтобы быть интеграторами (поэтому разрешающий контроллеру отклонить подобные шагу воздействия), если вы не задаете их в противном случае. Шум измерения обычно принимается, чтобы быть белым. Для получения дополнительной информации об объекте и возмущениях видят Модели Предсказания MPC и Настраивают Воздействие и Шумовые Модели.

    После создания mpc объект, хорошая практика должна использовать функции такой как cloffset вычислить устойчивое состояние замкнутого цикла выходная чувствительность, поэтому проверяя, может ли контроллер отклонить постоянные выходные воздействия. Более общее review также смотрит объект для потенциальных проблем. Чтобы выполнить более глубокую чувствительность и анализ робастности в течение периодов времени, в которые вы ожидаете, что никакое ограничение не будет активно, можно также преобразовать неограниченный контроллер в использование системного объекта LTI ss, zpk, или tf. Для связанных примеров см. Модель Анализа Прогнозирующий Контроллер для Проблем Устойчивости и Робастнесса, Тест диспетчер MPC Робастнесс, использующий MPC Designer, Вычислите Установившееся Усиление и Контроллер Извлечения.

    Обратите внимание на то, что многий из рекомендуемого выбора параметра включен в значения по умолчанию mpc объект; однако, начиная с каждого из них параметр обычно является результатом нескольких offs торговли проблемных зависимых, необходимо выбрать параметры, которые целесообразны для конкретного объекта и требований.

  4. Симулируйте замкнутый цикл — После того, как вы создаете контроллер MPC, вы обычно оцениваете эффективность своего контроллера путем симуляции его в замкнутом цикле с объектом с помощью одной из следующих опций.

    • Из командной строки MATLAB можно симулировать использование замкнутого цикла sim (более удобный для линейных моделей объекта управления) или mpcmove (более гибкий, допуская более общие объекты дискретного времени или сигналы воздействия).

    • От Simulink можно использовать блок MPC Controller (который берет mpc возразите в качестве параметра) в замкнутом цикле с вашей моделью объекта управления, созданной в Simulink. Эта опция допускает самую большую гибкость в симуляции более сложных систем и для легкой генерации производственного кода от вашего диспетчера.

    • MPC Designer позволяет вам симулировать ответ замкнутого цикла, одновременно настраивая параметры контроллера.

    Обратите внимание на то, что любая из этих опций позволяет вам также симулировать несоответствия модели (случаи, в которых фактический объект немного отличается от внутренней модели объекта управления, которую диспетчер использует для предсказания). Для связанного примера смотрите Симуляцию Контроллер MPC с Несоответствием Модели объекта управления. Когда ссылка и измеренные воздействия знаются заранее, MPC может использовать эту информацию (также известный как предвидение, или предварительно просматривающий), чтобы улучшать производительность контроллера. Смотрите Предварительный просмотр Сигнала для получения дополнительной информации и Улучшание Производительности Управления с Предвидением (Предварительный просмотр) для связанного примера. Точно так же можно задать настраивающиеся веса и ограничения, которые варьируются по горизонту предсказания. Для связанных примеров смотрите Ограничения Обновления во Время выполнения, Варьируйтесь Границы Ввода и вывода во Время выполнения, Веса Мелодии во Время выполнения, и Настройте Горизонты во Время выполнения.

  5. Совершенствуйте проект — После начальной оценки замкнутого цикла, обычно необходимо совершенствовать проект путем корректировки параметров контроллера и оценки различных сценариев симуляции. В дополнение к параметрам, описанным на шаге 3, можно рассмотреть:

  6. Убыстритесь выполнение — Смотрите диспетчера MPC Деплоймента.

  7. Развернитесь контроллер — Смотрите диспетчера MPC Деплоймента.

Управляйте нелинейными и изменяющимися во времени объектами

Часто объект, которым будут управлять, может быть точно аппроксимирован линейным объектом только локально вокруг данной рабочей точки. Это приближение больше не может быть точным как передачи времени и рабочая точка объекта (или параметры) изменения.

Можно использовать несколько подходов, чтобы иметь дело с этими случаями от более простого до более общего и сложного.

  1. Адаптивный MPC — Если порядок (и задержки) объекта не изменяется, можно спроектировать один контроллер MPC (например, для начальной рабочей точки), и затем во времени выполнения можно обновить модель предсказания контроллера на каждом временном шаге (в то время как контроллер все еще принимает, что модель предсказания остается постоянной в будущем через его горизонт предсказания).

    Обратите внимание на то, что, в то время как этот подход является самым простым, он требует, чтобы вы к постоянно (то есть, на каждом временном шаге) вычислили линеаризовавший объект, который должен быть предоставлен контроллеру. Можно сделать так тремя основными способами.

    1. Если у вас есть надежные нелинейные уравнения, описывающие объект, можно извлечь локальный линейный объект онлайн путем линеаризации уравнений, предположения, что этот процесс не является слишком в вычислительном отношении дорогим. Для примера с помощью этой стратегии смотрите Адаптивное MPC управление Нелинейным Химическим Реактором Используя Последовательную Линеаризацию

    2. В качестве альтернативы можно извлечь много линеаризовавших объектов оффлайн, покрыв соответствующие области входного пространства состояния, и затем онлайн можно использовать объект линейного варьирования параметра (LPV), который получает, интерполяцией, линейным объектом в текущей рабочей точке. Для примера с помощью этой стратегии смотрите Адаптивное MPC управление Нелинейным Химическим Реактором Используя Линейную Варьирующуюся по параметру Систему.

    3. Если объект точно не представлен математической моделью, но можно принять и устойчивость разомкнутого контура и минимальную сумму входного шума, можно использовать прошлые вводы и выводы объекта, чтобы оценить модель объекта онлайн, несмотря на то, что это может быть несколько в вычислительном отношении дорого. Для примера с помощью этой стратегии смотрите Адаптивное MPC управление Нелинейным Химическим Реактором Используя Онлайновую Оценку Модели.

    Этот подход требует mpc возразите и любой mpcmoveAdaptive функционируйте или блок Adaptive MPC Controller. Для получения дополнительной информации смотрите Адаптивный MPC и Модель, Обновляющую Стратегию.

  2. Линейное Время Различный MPC — Этим подходом является своего рода адаптивный MPC, в котором диспетчер знает заранее, как его внутренние изменения модели объекта управления в будущем, и поэтому используют эту информацию при вычислении оптимального управления через горизонт предсказания. Здесь, на каждом временном шаге, вы предоставляете контроллеру не только текущую модель объекта управления, но также и модели объекта управления для всех будущих шагов через целый горизонт предсказания. Чтобы вычислить модели объекта управления для будущих шагов, можно использовать переменные, которыми управляют, и состояния объекта, предсказанные контроллером MPC на каждом шаге как рабочие точки, вокруг которых может линеаризоваться нелинейная модель объекта управления.

    Этот подход особенно полезен, когда модель объекта управления значительно изменяется (но очевидно) в горизонте предсказания. Это требует mpc объект и использование mpcmoveAdaptive или блок Adaptive MPC Controller. Для получения дополнительной информации смотрите Изменяющийся во времени MPC.

  3. Запланированный на усиление MPC — В этом подходе вы проектируете несколько контроллеров MPC оффлайн, один для каждой соответствующей рабочей точки. Затем онлайн, вы переключаете активный контроллер, когда рабочая точка объекта изменяется. В то время как переключение контроллера в вычислительном отношении просто, этот подход требует более онлайновой памяти (и в общем больше конструкторской разработки), чем адаптивный MPC. Это должно быть зарезервировано для случаев, в которых линеаризовавшие модели объекта управления имеют различные порядки или задержки (и переключающаяся переменная медленно изменяется относительно динамики объекта). Использовать запланированный на усиление MPC. вы создаете массив mpc объекты и затем используют mpcmoveMultiple функционируйте или блок Multiple MPC Controllers для симуляции. Для получения дополнительной информации смотрите Запланированный на усиление MPC. Для примера смотрите Запланированное на усиление MPC управление Нелинейным Химическим Реактором.

  4. Нелинейный MPC — можно использовать эту стратегию управлять очень нелинейными объектами, когда все предыдущие подходы являются неподходящими, или когда необходимо использовать нелинейные ограничения или неквадратичные функции стоимости. Этот подход более в вычислительном отношении интенсивен, чем предыдущие единицы, и он также требует, чтобы вы спроектировали реализацию нелинейное средство оценки состояния, если состояние объекта не абсолютно доступно. Два нелинейных подхода MPC доступны.

    1. Многоступенчатый Нелинейный MPC — Для многоступенчатого контроллера MPC, каждый будущий шаг в горизонте (этап) имеет свои собственные переменные решения и параметры, а также свою собственную нелинейную стоимость и ограничения. Кардинально, стойте, и ограничительные функции на определенном этапе являются функциями только переменных решения и параметров на том этапе. В то время как определение нескольких затрат и ограничительных функций может потребовать большего количества времени проектирования, оно также допускает эффективную формулировку базовой задачи оптимизации и меньшей структуры данных, которая значительно уменьшает время вычисления по сравнению с типовым нелинейным MPC. Используйте этот подход, если ваша нелинейная проблема MPC стоила и ограничительные функции, которые не включают термины перекрестного этапа, как это часто бывает. Чтобы использовать многоступенчатый нелинейный MPC, необходимо создать nlmpcMultistage объект, и затем использует nlmpcmove функционируйте или блок Multistage Nonlinear MPC Controller для симуляции. Для получения дополнительной информации смотрите Многоступенчатый Нелинейный MPC.

    2. Типовой Нелинейный MPC — Этот метод является самым общим, и в вычислительном отношении дорогим, форма MPC. Когда это явным образом обеспечивает стандартные веса и линейные настройки границ, это может быть хорошая начальная точка для проекта, куда единственная нелинейность прибывает из модели объекта управления. Кроме того, можно использовать RunAsLinearMPC опция в nlmpc объект оценить, может ли линейный, время, варьируясь или адаптивный MPC достигнуть той же эффективности. Если так, используйте эти проектные решения, и возможно оцените усиление, запланированное MPC; в противном случае рассмотрите многоступенчатый нелинейный MPC. Используйте типовой нелинейный MPC только в качестве первоначального проекта, или когда все предыдущие проектные решения не будут жизнеспособны. Чтобы использовать типовой нелинейный MPC, необходимо создать nlmpc объект, и затем использует nlmpcmove функционируйте или блок Nonlinear MPC Controller для симуляции. Для получения дополнительной информации смотрите Типовой Нелинейный MPC.

Контроллер MPC развертывание

Когда вы удовлетворены эффективностью симуляции своего проектирования контроллера, вы обычно ищете способы ускорить выполнение, чтобы и оптимизировать проект для будущих симуляций и удовлетворять более строгие вычислительные требования встраиваемых приложений.

Можно использовать несколько стратегий улучшать вычислительную производительность контроллеров MPC.

  1. Попытайтесь увеличить шаг расчета — частота дискретизации должна быть достаточно высокой, чтобы покрыть значительную полосу пропускания системы. Однако, если шаг расчета слишком мал, мало того, что вы уменьшаете доступное время вычисления для контроллера, но необходимо также использовать больший горизонт предсказания, чтобы покрыть отклик системы, который увеличивает вычислительные требования.

  2. Попытайтесь сократить предсказание и горизонты управления — Поскольку и горизонты непосредственно влияют на общее количество переменных решения и ограничений в получившейся задаче оптимизации, они в большой степени влияют и на использование памяти и на количество необходимых вычислений. Поэтому проверяйте, можно ли получить подобные ответы отслеживания и робастность к неопределенности с более короткими горизонтами. Обратите внимание на то, что шаг расчета играет роль также. Частота дискретизации должна быть достаточно высокой (эквивалентно шаг расчета, достаточно маленький), чтобы покрыть значительную полосу пропускания системы. Однако, если шаг расчета слишком мал, не только у вас есть более короткое доступное время выполнения на оборудовании, но вам также нужно большее число шагов предсказания, чтобы покрыть отклик системы, который приводит к более в вычислительном отношении дорогой задаче оптимизации, которая будет решена на каждом временном шаге.

  3. Используйте различные параметры только при необходимости — Обычно, Model Predictive Control Toolbox™ позволяет вам варьироваться некоторые параметры (такие как веса или ограничительные коэффициенты) в инее запуска. В то время как эта возможность полезна в некоторых случаях, она значительно увеличивает сложность программного обеспечения. Поэтому, если в частности не необходимый, для развертывания, рассматривают явным образом определение таких параметров как константы, таким образом предотвращая возможность изменения их онлайн. Для связанных примеров смотрите Ограничения Обновления во Время выполнения, Варьируйтесь Границы Ввода и вывода во Время выполнения, Веса Мелодии во Время выполнения, и Настройте Горизонты во Время выполнения.

  4. Настройте решатель и его опции — решатель Model Predictive Control Toolbox по умолчанию является "плотным", "активный набор" решатель на основе алгоритма KWIK, и это обычно выполняет хорошо во многих случаях. Однако, если общее количество переменных, которыми управляют, выходных параметров и ограничений через целый горизонт является большим, вы можете рассмотреть использование решателя внутренней точки. Если внутренний объект является нестабильным очень разомкнутым контуром, рассмотрите использование разреженного решателя. Для обзора задачи оптимизации смотрите Задачу оптимизации. Для получения дополнительной информации о решателях см. Решатели QP и Сконфигурируйте Решатель Оптимизации для Нелинейного MPC. Для связанных примеров смотрите, Симулируют Контроллер MPC с Пользовательской Обработкой Туберкулеза Решателя и Оптимизации QP Используя Нелинейный MPC с Пользовательским Решателем.

Для приложения с чрезвычайно быстрым шагом расчета рассмотрите использование явного MPC. Можно доказать, что решение линейной проблемы MPC (квадратичная функция стоимости, линейный объект и ограничения) кусочно аффинный (PWA) на многогранниках. Другими словами, ограничения делят пространство состояний на многогранные "критические" области, в которых действие оптимального управления является аффинным (линейный плюс константа) функция состояния. Идея позади явного MPC состоит в том, чтобы предварительно вычислить, оффлайн и раз и навсегда, эти функции состояния для каждой области. Эти функции могут затем храниться в вашем контроллере. Во время выполнения контроллер затем выбирает и применяет соответствующий закон об обратной связи состояния, в зависимости от критической области, в которой находится текущая рабочая точка. Поскольку явные диспетчеры MPC не решают задачу оптимизации онлайн, они требуют намного меньшего количества расчетов и поэтому полезны для приложений, требующих времен небольшой выборки. С другой стороны, у них также есть намного больший объем потребляемой памяти. Действительно, чрезмерные требования к памяти могут представить этот подход, более не жизнеспособный для средних и крупных проблем. Кроме того, поскольку явный MPC предварительно вычисляет контроллер оффлайн, это не поддерживает обновления во время выполнения параметров, такие как веса, ограничения или горизонты.

Чтобы использовать явный MPC, необходимо сгенерировать explicitMPC объект от существующего mpc возразите и затем используйте mpcmoveExplicit функционируйте или блок Explicit MPC Controller для симуляции. Для получения дополнительной информации смотрите Явный MPC.

Итоговая опция, чтобы рассмотреть, чтобы улучшать вычислительную производительность и неявного и явного MPC должна упростить проблему. Некоторые параметры, такие как количество ограничений и переменных состояния номера, значительно увеличивают сложность получившейся задачи оптимизации. Поэтому, если предыдущие опции не удовлетворяют, рассматривают перенастройку этих параметров (и потенциально используйте более простую модель предсказания более низкой точности) упростить проблему.

Если вы удовлетворены вычислительной эффективностью своего проекта, можно сгенерировать код для развертывания на приложениях реального времени из MATLAB или Simulink. Для получения дополнительной информации смотрите, Генерируют Код и Развертывают Контроллер в Цели В реальном времени.

Документация Model Predictive Control Toolbox

Поддержка

Для просмотра документации необходимо авторизоваться на сайте