Вычислите оперативные индексы концентрации для портфеля
ci = concentrationIndices(PortfolioData)concentrationIndices функционируйте поддерживает следующие индексы:
CR — Отношение концентрации
Децили — Децили распределения весов портфеля
Gini — Коэффициент Gini
HH — индекс Херфиндаль-Хиршмана
HK — Индекс Ханны-Кея
HT — Индекс Холла-Тидемена
TE — индекс энтропии Theil
[ добавляют дополнительные аргументы пары "имя-значение". ci,Lorenz]
= concentrationIndices(___,Name,Value)
Вычислите индексы концентрации для кредитного портфеля с помощью портфеля, который описан его воздействиями. Воздействия в значении по умолчанию хранятся в EAD массив.
Загрузите CreditPortfolioData.mat файл, который содержит EAD используемый для PortfolioData входной параметр.
load CreditPortfolioData.mat
ci = concentrationIndices(EAD)ci=1×8 table
ID CR Deciles Gini HH HK HT TE
___________ ________ ___________ _______ ________ ________ ________ _______
"Portfolio" 0.058745 1x11 double 0.55751 0.023919 0.013363 0.022599 0.53485
Используйте CRIndex дополнительный вход, чтобы получить отношения концентрации для десятых и двадцатых по величине воздействий. В выходе, CR столбец становится вектором с одним значением для каждого требуемого индекса.
Загрузите CreditPortfolioData.mat файл, который содержит EAD используемый для PortfolioData входной параметр.
load CreditPortfolioData.mat ci = concentrationIndices(EAD,'CRIndex',[10 20])
ci=1×8 table
ID CR Deciles Gini HH HK HT TE
___________ __________________ ___________ _______ ________ ________ ________ _______
"Portfolio" 0.38942 0.58836 1x11 double 0.55751 0.023919 0.013363 0.022599 0.53485
Используйте HKAlpha дополнительный вход, чтобы установить альфа-параметр для Ханны-Кея (HK) индекс. Используйте вектор из альфа-значений, чтобы вычислить HK индексируйте для нескольких значений параметров. В выходе, HK столбец становится вектором с одним значением для каждого требуемого альфа-значения.
Загрузите CreditPortfolioData.mat файл, который содержит EAD используемый для PortfolioData входной параметр.
load CreditPortfolioData.mat ci = concentrationIndices(EAD,'HKAlpha',[0.5 3])
ci=1×8 table
ID CR Deciles Gini HH HK HT TE
___________ ________ ___________ _______ ________ ____________________ ________ _______
"Portfolio" 0.058745 1x11 double 0.55751 0.023919 0.013363 0.029344 0.022599 0.53485
Сравните меры по концентрации с помощью ID дополнительный аргумент для полностью разнообразного портфеля и полностью сконцентрированного портфеля.
ciD = concentrationIndices([1 1 1 1 1],'ID','Fully diversified'); ciC = concentrationIndices([0 0 0 0 5],'ID','Fully concentrated'); disp([ciD;ciC])
ID CR Deciles Gini HH HK HT TE
____________________ ___ ___________ ____ ___ ___ ___ ___________
"Fully diversified" 0.2 1x11 double 0 0.2 0.2 0.2 -2.2204e-16
"Fully concentrated" 1 1x11 double 0.8 1 1 1 1.6094
Используйте ScaleIndices дополнительный вход, чтобы масштабировать значения индекса Gini, HH, HK, HT, и TE. Область значений ScaleIndices от 0 через 1, независимый от количества кредитов.
ciDU = concentrationIndices([1 1 1 1 1],'ID','Diversified, unscaled'); ciDS = concentrationIndices([1 1 1 1 1],'ID','Diversified, scaled','ScaleIndices',true); ciCU = concentrationIndices([0 0 0 0 5],'ID','Concentrated, unscaled'); ciCS = concentrationIndices([0 0 0 0 5],'ID','Concentrated, scaled','ScaleIndices',true); disp([ciDU;ciDS;ciCU;ciCS])
ID CR Deciles Gini HH HK HT TE
________________________ ___ ___________ ____ __________ ___________ ___________ ___________
"Diversified, unscaled" 0.2 1x11 double 0 0.2 0.2 0.2 -2.2204e-16
"Diversified, scaled" 0.2 1x11 double 0 3.4694e-17 -3.4694e-17 -6.9389e-17 -1.3796e-16
"Concentrated, unscaled" 1 1x11 double 0.8 1 1 1 1.6094
"Concentrated, scaled" 1 1x11 double 1 1 1 1 1
Загрузите CreditPortfolioData.mat файл, который содержит EAD, используемый для PortfolioData входной параметр.
load CreditPortfolioData.mat
P = EAD;
ci = concentrationIndices(P);Визуализируйте аппроксимированную кривую Лоренца с помощью информации о децилях и также концентрации на уровне дециля.
Proportion = 0:0.1:1; figure; subplot(2,1,1) area(Proportion',[ci.Deciles' Proportion'-ci.Deciles']) axis([0 1 0 1]) title('Lorenz Curve (By Deciles)') xlabel('Proportion of Loans') ylabel('Proportion of Value') subplot(2,1,2) bar(diff(ci.Deciles)) axis([0 11 0 1]) title('Concentration by Decile') xlabel('Decile') ylabel('Weight')

Загрузите CreditPortfolioData.mat файл, который содержит EAD используемый для PortfolioData входной параметр. Дополнительный выход Lorenz содержит данные для точной кривой Лоренца.
load CreditPortfolioData.mat P = EAD; [~,Lorenz] = concentrationIndices(P); figure; area(Lorenz.ProportionLoans,[Lorenz.ProportionValue Lorenz.ProportionLoans-Lorenz.ProportionValue]) axis([0 1 0 1]) title('Lorenz Curve') xlabel('Proportion of Loans') ylabel('Proportion of Value')

PortfolioData — Неотрицательные положения портфеля в активах NНеотрицательные положения портфеля в активах N в виде N- 1 (или 1- N) числовой массив.
Типы данных: double
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
[ci,Lorenz] = concentrationIndices(PortfolioData,'CRIndex',100)CRIndex — Представляющий интерес индекс для отношения концентрацииПредставляющий интерес индекс для отношения концентрации в виде разделенной запятой пары, состоящей из 'CRIndex' и целочисленное значение между 1 и N, где N является количеством активов в портфеле. Значение по умолчанию для CRIndex 1 (CR по умолчанию самый большой вес портфеля). Если CRIndex вектор, отношение концентрации вычисляется для значения индекса в данном распоряжении.
Типы данных: double
HKAlpha — Альфа-параметр для индекса Ханны-КеяАльфа-параметр для Ханны-Кея индексирует в виде разделенной запятой пары, состоящей из 'HKAlpha', и положительное число, которое не может быть равно 1. Если HKAlpha вектор, индекс Ханны-Кея вычисляется для каждого альфа-значения в данном распоряжении.
Типы данных: double
ID — Пользовательский ID для портфеля"Portfolio" (значение по умолчанию) | вектор символов | представляет объект в виде строкиПользовательский ID для портфеля в виде разделенной запятой пары, состоящей из 'ID' и скалярный объект строки или вектор символов.
Типы данных: char | string
ScaleIndices — Отметьте, чтобы указать, масштабировать ли индексы концентрацииfalse (никакое масштабирование) (значение по умолчанию) | логический Отметьте, чтобы указать, масштабировать ли индексы концентрации в виде разделенной запятой пары, состоящей из 'ScaleIndices' и логический скаляр. Когда ScaleIndices установлен в истину, значение Gini, HH, HK, HT, и TE индексы масштабируются так, чтобы все эти индексы имели минимальное значение 0 (полная диверсификация) и максимальное значение 1 (полная концентрация).
Примечание
Масштабирование применяется только для портфелей по крайней мере с двумя активами. В противном случае масштабирующаяся возможность не определена.
Типы данных: логический
ci — Информация об индексах концентрации для данного портфеляИнформация об индексах концентрации для данного портфеля, возвращенного как таблица со следующими столбцами:
ID — Строка идентификатора портфеля. Используйте ID аргумент пары "имя-значение", чтобы установить его.
CR — Отношение концентрации. По умолчанию об отношении концентрации для первого индекса (самый большой вес портфеля) сообщают. Используйте CRIndex аргумент пары "имя-значение", чтобы выбрать различный индекс. Если CRIndex вектор из длины m, затем CR вектор-строка из размера 1- m. Для получения дополнительной информации смотрите Больше О.
Deciles — Децилями распределения весов портфеля является 1- 11 вектор-строка, содержащий значения 0, точки разделения на девять децилей и 1. Для получения дополнительной информации смотрите Больше О.
Gini — Коэффициент Gini. Для получения дополнительной информации смотрите Больше О.
HH — Индекс Херфиндаль-Хиршмана. Для получения дополнительной информации смотрите Больше О.
HK — Индекс Ханны-Кея (обратная величина). По умолчанию, 'alpha' параметр устанавливается на 0.5. Используйте HKAlpha аргумент пары "имя-значение", чтобы выбрать различное значение. Если HKAlpha вектор из lengthm, затем HK вектор-строка из размера 1- m. Для получения дополнительной информации смотрите Больше О.
HT — Индекс Холла-Тидемена. Для получения дополнительной информации смотрите Больше О.
TE — Индекс энтропии Theil. Для получения дополнительной информации смотрите Больше О.
Lorenz — Данные о кривой ЛоренцаДанные о кривой Лоренца, возвращенные как таблица со следующими столбцами:
ProportionLoans N+1)-by-1 числовой массив, содержащий значения 0, 1N, 2NNN= 1 . Это - данные для горизонтальной оси кривой Лоренца.
ProportionValue N+1)-by-1 числовой массив, содержащий пропорцию стоимости портфеля, накопленной до соответствующей пропорции кредитов в ProportionLoans столбец. Это - данные для вертикальной оси кривой Лоренца.
Все индексы концентрации для concentrationIndices примите кредитный портфель с воздействием контрагентов.
Позвольте P быть данным кредитным портфелем с воздействием контрагентов N. Позвольте x1... xN представляет подверженность каждому контрагенту с xi> = 0 для всего i = 1N. И, позвольте x быть общим воздействием портфеля
Примите тот x> 0, то есть, по крайней мере одно воздействие является ненулевым. Веса портфеля даны w1..., wN с
Веса сортируются в не уменьшающемся порядке. Следующее стандартное обозначение использует скобки вокруг индексов, чтобы обозначить упорядоченный значения.
concentration ratio (CR) отвечает на вопрос, “какая пропорция суммы обязательств накапливается в самых больших кредитах k?”
Формула для отношения концентрации (CR):
Например, если k =1, CR1 является суммой одного термина w[N-1+1] = w[N], то есть, это - самый большой вес. Для любого k индекс CR принимает значения от 0 через 1.
Lorenz curve является визуализацией совокупной пропорции стоимости портфеля (или совокупные веса портфеля) против совокупной пропорции кредитов.
Совокупная пропорция кредитов (p) задана:
Совокупная пропорция стоимости портфеля L задана как:
Кривая Лоренца является графиком L по сравнению с p или совокупной пропорцией стоимости портфеля по сравнению с совокупной пропорцией количества кредитов (отсортированный от самого маленького до самого большого).
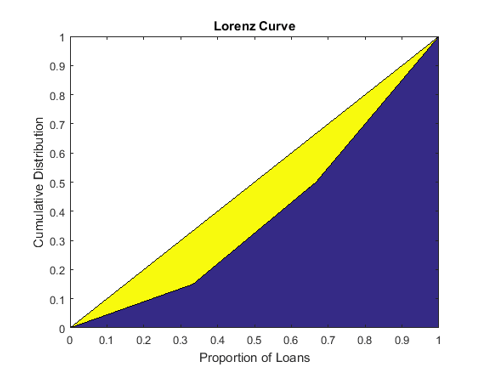
Диагональная линия обозначается в том же графике, потому что это представляет кривую для портфеля с наименее возможной концентрацией (все кредиты с тем же весом). Областью между диагональю и кривой Лоренца является визуальное представление коэффициента Gini, который является другой мерой по концентрации.
Deciles обычно используется в контексте неравенства доходов.
Если вы сортируете индивидуумов по их уровню дохода, какая пропорция совокупного дохода заработана на самые низкие 10% и самые низкие 20% населения? В кредитном портфеле кредиты могут быть отсортированы по воздействию. Первый дециль соответствует пропорции стоимости портфеля, которая накапливается самыми маленькими 10%-ми кредитами и так далее. Децили являются пропорциями, поэтому они всегда принимают значения от 0 через 1.
При определении совокупной пропорции кредитов (p) и совокупная пропорция значений L как в Лоренце Курве, децили являются подмножеством пропорции массива значения. Учитывая индексы d1, d2, …, d9, таким образом, что пропорция кредитов совпадает точно с этими значениями:
Децили D 0, D 1...., D 9, D 10 заданы как соответствующая пропорция значений:
Когда общее количество кредитов, N не является делимым 10, никакие индексы, совпадает с точной пропорцией кредитов 0.1, 0.2, и так далее. В этом случае значения дециля линейно интерполированы из данных о кривой Лоренца (то есть, из p и массивов L). С этим определением существует 11 значений в информации о децилях, потому что конечные точки 0% и 100% включены.
Gini index (или коэффициент) визуализируется на графике кривой Лоренца как область между диагональю и кривой Лоренца.
Технически, индекс Gini является отношением той области к области полного треугольника под диагональю на графике кривой Лоренца. Индекс Gini также задан эквивалентно как средняя абсолютная разность между всеми весами в портфеле, нормированном на средний вес.
Используя пропорцию значений, которые массив L, заданный в разделе кривой Лоренца, индекс Gini, дан формулой:
Эквивалентно, индекс Gini может быть вычислен из отсортированных весов непосредственно с формулой:
Содействующие значения Gini всегда между 0 (полная диверсификация) и 1– 1/N (полная концентрация).
Herfindahl-Hirschman index обычно используется в качестве меры концентрации рынка.
Формула для индекса Херфиндаль-Хиршмана:
Индекс Херфиндаль-Хиршмана принимает значения между 1/N (полная диверсификация) и 1 (полная концентрация).
Hannah-Kay index является обобщением индекса Херфиндаль-Хиршмана.
Формула для Ханны-Кея зависит от параметра α> 0, α ≠ 1, можно следующим образом:
Эта формула является обратной величиной исходного индекса Ханны-Кея, который задан с 1/(1− α) в экспоненте. Для анализа концентрации взаимная формула является стандартом, потому что это увеличивается, как концентрация увеличивается. Это - формула, реализованная в concentrationIndices. Индекс Ханны-Кея принимает значения между 1/N (полная диверсификация) и 1 (полная концентрация).
Hall-Tideman index является мерой, обычно используемой для концентрации рынка.
Формула для индекса Холла-Тидемена:
Индекс Холла-Тидемена принимает значения между 1/N (полная диверсификация) и 1 (полная концентрация).
Theil entropy index, на основе традиционной энтропийной меры (например, шенноновская энтропия), настроен так, чтобы это увеличилось как концентрация, увеличивается (энтропийные перемещения в противоположном направлении), и переключенный, чтобы сделать его положительным.
Формула для индекса энтропии Theil:
Энтропийный индекс Theil принимает значения между 0 (полная диверсификация) и log(N) (полная концентрация).
[1] Базельский Комитет по Банковскому надзору. "Исследования Концентрации Кредитного риска". Рабочий документ № 15. Ноябрь 2006.
[2] Calabrese, R. и Ф. Порро. "Концентрация одно имени рискует в кредитных портфелях: сравнение индексов концентрации". рабочий документ 201214, Институт Geary, Университетский Колледж, Дублин, май 2012.
[3] Lütkebohmert, E. Риск концентрации в кредитных портфелях. Спрингер, 2009.
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.