Используя Communications Toolbox™ можно реализовать исчезающие объекты использования каналов или блоки. Rayleigh и Rician, исчезающий каналы, являются полезными моделями явлений реального мира в радиосвязях. Эти явления включают многопутевые эффекты рассеивания, дисперсию времени и эффекты Доплера, которые являются результатом относительного движения между передатчиком и приемником. В этом разделе приведены краткий обзор исчезающих каналов и описывает, как реализовать их использующий тулбокс.
Этот рисунок изображает прямые и крупнейшие отраженные пути между стационарным радио-передатчиком и движущимся приемником. Теневые формы представляют отражатели, такие как создания.
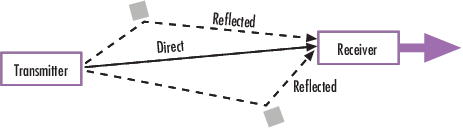
Крупнейшие пути приводят к прибытию задержанных версий сигнала в приемнике. Кроме того, радио-сигнал подвергается рассеиванию по локальной шкале для каждого крупнейшего пути. Такое локальное рассеивание обычно следует из отражений от объектов около мобильного телефона. Эти неразрешимые компоненты объединяются в приемнике и вызывают явление, известное как многопутевое исчезновение. Из-за этого явления, каждый крупнейший путь ведет себя как дискретный исчезающий путь. Как правило, процесс исчезновения характеризуется Распределением Релея для не пути угла обзора и распределением Rician для пути угла обзора.
Относительное движение между передатчиком и приемником вызывает эффекты Доплера. Локальное рассеивание обычно прибывает из многих углов вокруг мобильного телефона. Этот сценарий вызывает область значений эффектов Доплера, известных как Доплеровский спектр. Максимальный эффект Доплера соответствует локальным компонентам рассеивания, направление которых точно выступает против траектории мобильного телефона.
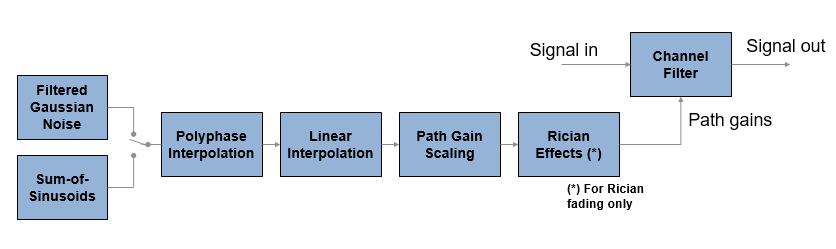
Фильтр канала применяет усиления пути к входному сигналу, Signal in. Усиления пути сконфигурированы на основе настроек, выбранных в исчезающем объекте канала или блоке.
Эти блоки и объекты включают вам к модели SISO или MIMO, исчезающей каналы.
| Инструмент | SISO | MIMO |
|---|---|---|
| MATLAB® | ||
| Simulink® |
Основополосная модель канала для многопутевых сценариев распространения, что вы реализуете объекты использования, включает:
N дискретные исчезающие пути. Каждый путь имеет свою собственную задержку и среднее усиление степени. Канал, для которого N = 1 называется плоским частотой исчезающим каналом. Канал, для которого N> 1 испытан как выборочный частотой исчезающий канал сигналом достаточно широкой полосы пропускания.
Модель Rayleigh или Rician для каждого пути.
Моделирование пути к каналу по умолчанию с помощью спектра Джейкса Доплера, эффект Доплера имеющий, который может быть задан. Другие типы Доплеровских позволенных спектров (идентичный или отличающийся для всех путей) включают: плоский, ограниченный Jakes, асимметричный Jakes, Гауссов, bi-Gaussian, округленный, и звонок.
Если максимальный эффект Доплера установлен в 0 или не использован во время конструкции объекта канала, то объектные модели канал как статический. Для этой настройки исчезновение не развивается со временем, и Доплеровский заданный спектр не оказывает влияния на процесс исчезновения.
Некоторая дополнительная информация о типичных значениях для задержек и усилений находится в Выборе Realistic Channel Property Values.
Библиотека блоков Каналов включает MIMO и блоки исчезновения SISO, которые могут симулировать явления реального мира в мобильной связи. Эти явления включают многопутевые эффекты рассеивания, в дополнение к эффектам Доплера, которые являются результатом относительного движения между передатчиком и приемником.
Совет
Чтобы смоделировать канал, который включает и исчезновение и аддитивный белый Гауссов шум, используйте исчезающий блок канала, сопровождаемый блоком AWGN Channel.
MIMO Fading Channel и блоки SISO Fading Channel могут быть установлены в распределения замираний модели Rayleigh или Rician канала. На основе типа пути прохождения сигнала выберите распределение замираний, чтобы использовать.
| Путь прохождения сигнала | Распределение замираний |
|---|---|
| Прямой путь угла обзора с передатчика на приемник | Rician |
| Один или несколько крупнейших отраженных путей с передатчика на приемник | Rayleigh |
Можно использовать один экземпляр исчезающего блока канала, сконфигурированного для распределения Релеевского замирания, чтобы смоделировать несколько крупнейших отраженных путей одновременно.
Выбор соответствующих параметров блоков для вашей ситуации важен. Для получения дополнительной информации смотрите Realistic Channel Property Values Выбора и страницы с описанием блока MIMO Fading Channel и SISO Fading Channel.
Можно просмотреть характеристики исчезающего канала с помощью инструментов визуализации канала. Для получения дополнительной информации смотрите Визуализацию Канала.
Система связи, включающая исчезающий канал обычно, требует компонентов, которые компенсируют исчезающий ответ. Типичные подходы, чтобы компенсировать исчезновение включают:
Дифференциальная модуляция или эквалайзер с одним касанием помогают компенсировать плоский частотой исчезающий канал. Для получения информации о реализации дифференциальной модуляции смотрите страницу с описанием блока M-DPSK Modulator Baseband.
Эквалайзер с несколькими касаниями помогает компенсировать выборочный частотой исчезающий канал. Смотрите Эквализацию для получения дополнительной информации.
Адаптивная Эквализация с Фильтрацией и Исчезающим примером Канала иллюстрирует, почему компенсация исчезающего канала необходима.
Rayleigh и Rician многопутевые исчезающие средства моделирования канала в Communications Toolbox используют ограниченную полосой дискретную многопутевую модель канала раздела 9.1.3.5.2 в [1]. Эта реализация принимает, что профиль степени задержки и Доплеровский спектр канала отделимы [1]. Многопутевой исчезающий канал поэтому моделируется как линейный фильтр конечной импульсной характеристики (FIR). Пусть обозначьте набор выборок во входе к каналу. Затем выборки при выходе канала связаны с через:
где набор весов касания, данных:
В уравнениях:
входной период расчета к каналу.
, где , набор задержек пути. K является общим количеством путей в многопутевом исчезающем канале.
, где , набор усилений сложного контура многопутевого исчезающего канала. Эти усиления пути являются некоррелироваными друг с другом.
и выбраны так, чтобы мал, когда n меньше или больше, чем .
Два метода, отфильтрованный Гауссов шум и сумма синусоид, используются, чтобы сгенерировать набор усилений сложного контура, .
Каждый процесс усиления пути сгенерирован следующими шагами:
Фильтрованный гауссов шумовой метод
Комплексный некоррелированый (белый) Гауссов процесс с нулевым средним значением и модульным отклонением сгенерирован в дискретное время.
Комплексный Гауссов процесс отфильтрован Доплеровским фильтром с частотной характеристикой , где обозначает желаемый Доплеровский спектр мощности.
Отфильтрованный комплексный Гауссов процесс интерполирован так, чтобы его период расчета был сопоставим с периодом расчета входного сигнала. Комбинация линейной и многофазной интерполяции используется.
Метод суммы синусоид
Взаимно некоррелированые формы волны Релеевского замирания сгенерированы с помощью метода, описанного в [2], где i = 1 соответствует синфазному компоненту, и i = 2 соответствует квадратурному компоненту.
Где
Nk указывает, что количество синусоид раньше моделировало один путь.
дискретная Доплеровская частота и вычисляется для каждого компонента синусоиды в одном пути.
фаза n th компонент и i.i.d. случайная переменная, имеющая равномерное распределение на интервале .
t является временем процесса исчезновения.
При моделировании спектра Джейкса Доплера, дискретных Доплеровских частот, , с максимальным сдвигом f макс. дают
где
Чтобы усовершенствовать процесс исчезновения вовремя, начальный параметр времени, t init, введен. Исчезающие формы волны становятся
Когда t init = 0, процесс исчезновения запускается в начальный момент времени. Положительное значение t init совершенствует процесс исчезновения относительно начального момента времени при поддержании его непрерывности.
Канал, исчезающий выборки, сгенерирован с помощью алгоритма GMEDS1 [2] .
Вычислите комплексные коэффициенты
Комплексный процесс, следующий из любого метода, , масштабируется, чтобы получить правильное среднее усиление пути. В случае Рэлеевского канала процесс исчезновения получен как:
где
В случае канала Rician процесс исчезновения получен как:
где K-фактор Rician k th путь, эффект Доплера компонента угла обзора k th путь (в Гц), и начальная фаза компонента угла обзора k th путь (в рад).
Во входе к ограниченной полосой многопутевой модели канала переданные символы должны быть сверхдискретизированы фактором, по крайней мере, равняются фактору расширения полосы пропускания, введенному импульсным формированием. Например, если sinc импульсное формирование используется, для которого полоса пропускания сигнала импульсной формы равна уровню символа, затем фактор расширения полосы пропускания равняется 1, и по крайней мере одна выборка на символ требуется во входе к каналу. Если фильтр повышенного косинуса (RC) с фактором, больше чем 1 используется, для которого полоса пропускания сигнала импульсной формы равна дважды уровню символа, то фактор расширения полосы пропускания равняется 2 и по крайней мере двум выборкам на символ, требуется во входе к каналу.
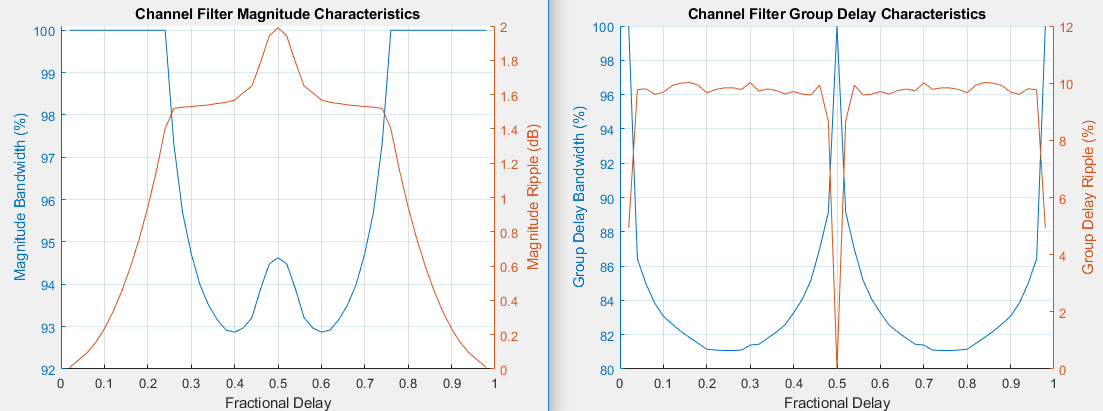
Фильтр канала реализует полосовой фильтр конечной импульсной характеристики (FIR) дробной задержки (FD) с длиной 16 коэффициентов для каждого кандидата дробная задержка в 0, 0.02, 0.04, …, 0.98.
Каждый дискретный путь округлен его самому близкому кандидату дробная задержка, таким образом, предел погрешности задержки составляет 1% шага расчета. Чтобы достигнуть полосы пропускания групповой задержки чрезмерные 80% и полосы пропускания величины чрезмерные 90%, алгоритм выбирает оптимальные КИХ-содействующие значения для каждой дробной задержки при удовлетворении следующим критериям:
Пульсация групповой задержки ≤ 10%
Пульсация величины ≤ 2 дБ
Величина bandedge затухание = 3 дБ
Графики показывают полосы пропускания, которые удовлетворяют критериям расчета для пульсации групповой задержки, пульсации величины и величины bandedge затухание.
[1] Jeruchim, член конгресса, Балабан, P. и Shanmugan, K. S. симуляция систем связи, Секонд-Эдайшн, Нью-Йорк, академический Kluwer / пленум, 2000.
[2] Pätzold, Мэттиас, Cheng-Сянцзян Ван и Бьорн Олав Хогштанд. “Две Новых Суммы основанных на синусоидах Методов для Эффективной Генерации Нескольких Некоррелированых Форм волны Релеевского замирания”. Транзакции IEEE на Радиосвязях. Издание 8, Номер 6, 2009, стр 3122–3131.
Communications Toolbox моделирует исчезающий канал как линейный КИХ-фильтр. Фильтрация сигнала с помощью исчезающего канала включает эти шаги:
Создайте объект канала, который описывает канал, который вы хотите использовать. Объект канала является типом переменной MATLAB, которая содержит информацию о канале, таком как максимальный эффект Доплера.
Настройте свойства объекта канала, при необходимости, адаптировать его в соответствии с вашими потребностями. Например, можно изменить задержки пути или средние усиления пути.
Примените объект канала к своему использованию сигнала, вызвав объект.
В этом разделе описывается задать, смотреть, и управлять объектами канала. Темы:
Чтобы создать исчезающий объект канала, подходящий для вашей ситуации с моделированием, выберите один из этих Системных объектов.
| Функция | Объект | Смоделированная ситуация |
|---|---|---|
| Объект канала с релеевским замиранием | Один или несколько крупнейших отраженных путей | |
| Rician, исчезающий объект канала | Один прямой путь угла обзора, возможно объединенный с одним или несколькими крупнейшими отраженными путями |
Например, эта команда создает объект канала представление Канала с релеевским замиранием, который действует на сигнал, произведенный на уровне 100 000 Гц. Максимальный эффект Доплера канала составляет 130 Гц.
rayChan1 = comm.RayleighChannel('SampleRate',1e5,...
'MaximumDopplerShift',130); % Rayleigh fading channel object
Изучить, как вызвать rayChan1 исчезающий объект канала пропустить переданный сигнал через канал, смотрите Используя Исчезающие Каналы.
Можно также создать другой объект путем дублирования существующего объекта и затем настроить свойства нового объекта при необходимости. Чтобы скопировать объект всегда используют clone функционируйте, такие как:
rayChan2 = clone(rayChan1); % Copy rayChan1 to create an independent rayChan2.
вместо rayChan2 = rayChan1. clone команда создает копию rayChan1 это независимо от rayChan1. В отличие от этого, команда rayChan2 = rayChan1 создает rayChan2 как просто ссылка на rayChan1, так, чтобы rayChan1 и rayChan2 всегда имейте неразличимое содержимое.
Объект канала имеет многочисленные свойства, которые записывают информацию о модели канала о состоянии канала, который уже отфильтровал сигнал, и об операции канала на будущем сигнале.
Можно просмотреть свойства этими способами:
Чтобы просмотреть все свойства объекта канала, введите имя объекта в Командном окне.
Можно просмотреть свойство объекта канала или присвоить значение переменной путем ввода имени объекта, сопровождаемого точкой (период), сопровождаемый под названием свойство.
Можно изменить перезаписываемые свойства объекта канала этими способами:
Чтобы изменить значение по умолчанию свойства объекта канала, введите требуемое значение в синтаксис создания объекта.
Чтобы изменить значение writeable свойства объекта канала, выпустите оператор присваивания, который использует запись через точку на объекте канала. А именно, запись через точку означает выражение, которое состоит из имени объекта, сопровождаемого точкой, сопровождаемой под названием свойство.
Отобразите рэлеевские свойства объектов канала
Создайте Рэлеевский объект канала. Отобразите объект показать свойства, инициализированные по умолчанию, и те задали при создании объекта. Ввод rayChan отображения все свойства объекта канала. Некоторые значения свойств были присвоены, когда объект был создан, в то время как другие свойства имеют значения по умолчанию. Для получения дополнительной информации об определенных свойствах канала, смотрите страницу с описанием для comm.RayleighChannel объект.
rayChan = comm.RayleighChannel('SampleRate',1e5,'MaximumDopplerShift',130); rayChan % View all the properties
rayChan =
comm.RayleighChannel with properties:
SampleRate: 100000
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 130
DopplerSpectrum: [1x1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
g = rayChan.AveragePathGains % Retrieve the AveragePathGains property of rayChang = 0
Настройте свойства объектов канала Rician
Rician, исчезающий, объект канала имеет дополнительное свойство, которое не появляется для объекта Канала с релеевским замиранием, а именно, скалярного KFactor свойство. Для получения дополнительной информации о свойствах канала Rician, смотрите страницу с описанием для comm.RicianChannel объект.
Измените свойства объектов канала Rician
Создайте объект канала Rician. Настройка по умолчанию для Visualization свойством является 'Off'. Изменение настройки по умолчанию к 'Impulse response' генерирует график импульсной характеристики выходного сигнала, когда объект называется. Выход отображает подмножество всех свойств объекта канала. Выберите all properties видеть полный набор свойств для ricChan.
ricChan= comm.RicianChannel; % Create object ricChan.Visualization = 'Impulse response' % Enables the impulse response channel visualization
ricChan =
comm.RicianChannel with properties:
SampleRate: 1
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
KFactor: 3
DirectPathDopplerShift: 0
DirectPathInitialPhase: 0
MaximumDopplerShift: 1.0000e-03
DopplerSpectrum: [1x1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
Некоторые свойства объекта канала связаны друг с другом таким образом, что, когда значение одного свойства изменяется, значение другого свойства должно измениться некоторым соответствующим способом сохранить объект канала сопоставимым. Например, если вы изменяете длину вектора PathDelays, затем значение AveragePathGains должен измениться так, чтобы его длина вектора равнялась длине вектора нового значения PathDelays. Это вызвано тем, что длина каждого из этих двух векторов равняется количеству дискретных путей канала. Для получения дополнительной информации о соединенных свойствах и примере, смотрите comm.RayleighChannel или comm.RicianChannel.
Доплеровский спектр объекта канала задан через его DopplerSpectrum свойство. Значение этого свойства должно быть также:
Доплеровская структура спектра. В этом случае тот же Доплеровский спектр применяется к каждому пути объекта канала.
Массив ячеек Доплеровских структур спектра той же длины как PathDelays векторное свойство. В этом случае Доплеровский спектр каждого пути дан соответствующей Доплеровской структурой спектра в векторе.
Когда длина вектора PathDelays свойство увеличено, длина DopplerSpectrum автоматически увеличен, чтобы совпадать с длиной PathDelays, путем добавления структур спектра Джейкса Доплера.
Если длина PathDelays векторное свойство уменьшено, длина DopplerSpectrum автоматически уменьшен, чтобы совпадать с длиной PathDelays, путем удаления последних Доплеровских структур спектра.
Доплеровская структура спектра содержит свойства, используемые, чтобы охарактеризовать Доплеровский спектр, но максимальный эффект Доплера является свойством объекта канала. В этом разделе описывается создать и управлять Доплеровскими структурами спектра, и как присвоить их DopplerSpectrum свойство объектов канала.
Чтобы создать Доплеровские структуры спектра, используйте doppler функция. Единственная цель doppler функция должна создать Доплеровские структуры спектра, используемые, чтобы задать значение DopplerSpectrum свойство объектов канала. Выберите из следующего:
doppler('Jakes')
doppler('Flat')
doppler('Rounded', ...)
doppler('Bell', ...)
doppler('Asymmetric Jakes', ...)
doppler('Restricted Jakes', ...)
doppler('Gaussian', ...)
doppler('BiGaussian', ...)
Например, Гауссов спектр с нормированным (максимальным эффектом Доплера канала) стандартное отклонение 0,1, может быть создан как:
dopp1 = doppler('Gaussian',0.1);Примечание
При создании Доплеровской структуры спектра рассмотрите следующие зависимости:
Если вы присваиваете одну Доплеровскую структуру спектра DopplerSpectrum, все пути имеют заданный Доплеровский спектр того же самого.
Если FadingTechnique свойством является 'Sum of sinusoids', DopplerSpectrum должен быть doppler('Jakes');
Если вы присваиваете массив ячейки строки различных Доплеровских структур спектра к DopplerSpectrum, каждому пути задала Доплеровский спектр соответствующая структура в массиве ячеек. В этом случае, длина DopplerSpectrum должно быть равно длине PathDelays.
Чтобы сгенерировать код С, задайте DopplerSpectrum к одной Доплеровской структуре спектра.
Создайте Доплеровскую структуру спектра путем определения типа Доплеровского спектра как 'Rounded', затем измените настройки полиномиального типа
Округленная Доплеровская структура спектра со свойствами по умолчанию создана и отображена, и третий элемент Polynomial поле изменяется.
doppRound = doppler('Rounded')doppRound = struct with fields:
SpectrumType: 'Rounded'
Polynomial: [1 -1.7200 0.7850]
Настройте третий коэффициент полинома.
doppRound.Polynomial(3) = 0.825
doppRound = struct with fields:
SpectrumType: 'Rounded'
Polynomial: [1 -1.7200 0.8250]
Следует иметь в виду, что возможно изменить Доплеровскую структуру спектра к недопустимой настройке. Валидация Доплеровских настроек структуры спектра выполняется, когда структура используется исчезающим объектом канала. doppRound структура спектра, заданная выше, допустима.
ricianCh = comm.RicianChannel('DopplerSpectrum',doppRound)ricianCh =
comm.RicianChannel with properties:
SampleRate: 1
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
KFactor: 3
DirectPathDopplerShift: 0
DirectPathInitialPhase: 0
MaximumDopplerShift: 1.0000e-03
DopplerSpectrum: [1x1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
DopplerSpectrum свойство объекта канала может быть изменено путем присвоения ему Доплеровской структуры спектра или вектора из Доплеровских структур спектра.
В этом примере показано, как изменить значение по умолчанию, спектр Джейкса Доплера сконфигурированного Рейли образовывает канал объект к плоскому Доплеровскому спектру.
Создайте Рэлеевский объект канала
Установите частоту дискретизации на 9 600 Гц и максимальный эффект Доплера к 100 Гц.
rayChan = comm.RayleighChannel( ... 'SampleRate',9600,'MaximumDopplerShift',100)
rayChan =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
rayChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Jakes'
Измените Доплеровский спектр
Создайте плоскую Доплеровскую структуру спектра, и затем присвойте ее в rayChan объект.
doppFlat = doppler('Flat')doppFlat = struct with fields:
SpectrumType: 'Flat'
rayChan.DopplerSpectrum = doppFlat
rayChan =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
rayChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Flat'
В этом примере показано, как изменить значение по умолчанию, спектр Джейкса Доплера сконфигурированного Rician образовывает канал объект к Гауссову Доплеровскому спектру с нормированным стандартным отклонением 0,3. Затем отобразите DopplerSpectrum свойство и изменение нормированное стандартное отклонение Доплеровского спектра к 1,1.
Создайте объект канала Rician
Установите частоту дискретизации на 9 600 Гц, максимальный эффект Доплера к 100 Гц и K-фактор к 2.
ricChan = comm.RicianChannel( ... 'SampleRate',9600,'MaximumDopplerShift',100,'KFactor',2)
ricChan =
comm.RicianChannel with properties:
SampleRate: 9600
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
KFactor: 2
DirectPathDopplerShift: 0
DirectPathInitialPhase: 0
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
ricChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Jakes'
Измените Доплеровский спектр
Создайте Гауссову Доплеровскую структуру спектра с нормированным стандартным отклонением 0,3 и присвойте его в ricChan объект.
doppGaus = doppler('Gaussian',0.3)doppGaus = struct with fields:
SpectrumType: 'Gaussian'
NormalizedStandardDeviation: 0.3000
ricChan.DopplerSpectrum = doppGaus
ricChan =
comm.RicianChannel with properties:
SampleRate: 9600
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
KFactor: 2
DirectPathDopplerShift: 0
DirectPathInitialPhase: 0
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
ricChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Gaussian'
NormalizedStandardDeviation: 0.3000
ricChan.DopplerSpectrum.NormalizedStandardDeviation = 1.1; ricChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Gaussian'
NormalizedStandardDeviation: 1.1000
В этом примере показано, как изменить значение по умолчанию спектр Джейкса Доплера сконфигурированного Рейли с тремя путями образовывают канал объект к массиву ячеек различных Доплеровских спектров, и затем изменить свойства Доплеровского спектра третьего пути.
Создайте Рэлеевский объект канала
Установите частоту дискретизации на 9 600 Гц, максимальный эффект Доплера к 100 Гц, и задайте задержки пути 0, 1e-4, и 2.1e-4 seconds.
rayChan = comm.RayleighChannel( ... 'SampleRate',9600, ... 'MaximumDopplerShift',100, ... 'PathDelays',[0 1e-4 2.1e-4])
rayChan =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: [0 1.0000e-04 2.1000e-04]
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
rayChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Jakes'
Измените Доплеровский спектр
Задайте DopplerSpectrum свойство как массив ячеек с независимым Доплеровским спектром для каждого пути.
rayChan.DopplerSpectrum = {doppler('Flat') doppler('Flat') doppler('Rounded')}rayChan =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: [0 1.0000e-04 2.1000e-04]
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: {[1x1 struct] [1x1 struct] [1x1 struct]}
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
rayChan.DopplerSpectrum{:}ans = struct with fields:
SpectrumType: 'Flat'
ans = struct with fields:
SpectrumType: 'Flat'
ans = struct with fields:
SpectrumType: 'Rounded'
Polynomial: [1 -1.7200 0.7850]
Измените Polynomial свойство для третьего пути.
rayChan.DopplerSpectrum{3}.Polynomial = [1 -1.21 0.7]rayChan =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: [0 1.0000e-04 2.1000e-04]
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: {[1x1 struct] [1x1 struct] [1x1 struct]}
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
rayChan.DopplerSpectrum{:}ans = struct with fields:
SpectrumType: 'Flat'
ans = struct with fields:
SpectrumType: 'Flat'
ans = struct with fields:
SpectrumType: 'Rounded'
Polynomial: [1 -1.2100 0.7000]
Прежде чем вы отфильтруете сигнал с помощью объекта канала, убедитесь, что свойства канала имеют подходящие значения для ситуации, которую вы хотите смоделировать. Этот раздел предлагает некоторые инструкции, чтобы помочь вам выбрать реалистические значения, которые подходят для ваших потребностей моделирования. Темы
Синтаксисы для просмотра и изменения значений свойств объектов канала описаны в Определении Исчезающего Канала.
Вот некоторые советы для выбора значений свойств, которые описывают реалистические каналы:
Задержки пути
Условно, первая задержка обычно обнуляется. Первая задержка соответствует первому прибывающему пути.
Для внутренних сред задержки пути после того, как первые обычно между 1e-9 секундами и 1e-7 секундами.
Для наружных сред задержки пути после того, как первые обычно между 1e-7 секундами и 1e-5 секундами. Большие задержки этой области значений могут соответствовать, например, к области, окруженной горами.
Способность сигнала разрешить дискретные пути связана со своей полосой пропускания. Если различие между самыми большими и самыми маленькими задержками пути меньше приблизительно 1% символьного периода, то сигнал испытывает канал, как будто это имело только один дискретный путь.
Средние усиления пути
Средние усиления пути в объекте канала указывают на среднее усиление степени каждого исчезающего пути. На практике среднее значение усиления пути является большим отрицательным значением дБ. Однако модели компьютера обычно используют средние усиления пути в области значений [-20, 0] дБ.
Значения дБ в векторе из средних усилений пути часто затухают примерно линейно в зависимости от задержки, но определенный профиль задержки зависит от среды распространения.
Чтобы гарантировать, что ожидаемая общая степень объединенных усилений пути равняется 1, можно нормировать усиления пути через NormalizePathGains свойство объекта канала.
Максимальные эффекты Доплера
Эффекты Доплера заданы в терминах относительной скорости между передатчиком и приемником. Максимальный эффект Доплера в Герц, f d = vf ∕ c. В формуле v является относительной скоростью в m/s, f является несущей частотой передачи в Герц, и c является скоростью света (3×108 m/s). Относительная скорость является величиной без направленной информации.
Примените максимальную формулу эффекта Доплера, принимающую несущую частоту передачи 900 МГц, автомобиль, перемещающийся на скорости автострады и идущем пешеходе. Сигнал, переданный от автомобиля, перемещающегося на скорости автострады к стационарному приемнику, испытал бы максимальный эффект Доплера приблизительно 80 Гц. Сигнал, переданный с мобильного телефона, сохраненного идущим пешеходом к стационарному приемнику, испытал бы максимальный эффект Доплера приблизительно 4 Гц.
Максимальный эффект Доплера 0 соответствует статическому каналу, который прибывает из распределения Rayleigh или Rician.
Доплер Спектрум
K-фактор для Rician исчезающие каналы
K-фактор Rician задает отношение зеркальной-к-рассеянному степени для прямого пути угла обзора. Отношение описывается линейно, не в дБ.
Для исчезновения Rician K-фактор обычно находится в области значений [1, 10].
K-фактор 0 соответствует Релеевскому замиранию.
Эффект Доплера пути угла обзора (LOS) для Rician исчезающие каналы
Эффект Доплера пути к LOS Rician, также известный как прямой эффект Доплера пути, задает относительное движение пути к LOS между передатчиком и приемником.
Эффект Доплера пути к LOS Rician в Герц, f d_los = (u ⋅w) × f ∕ c. В формуле, (u ⋅w) скалярное произведение векторов u и w, u является нормированным путем к LOS от передатчика к приемнику, w является скоростью приемника относительно передатчика, f является несущей частотой передачи в Герц, и c является скоростью света (3×108 m/s).
Примените эту формулу для несущей частоты передачи 900 МГц при заданной относительной скорости. Для сигнала от передатчика в координатном начале координат, которое достигает приемника в координате [100 100 0], где относительная скорость между передатчиком и приемником w = [3 - 6 0.1]. Эффект Доплера пути к LOS составляет 4,25 Гц.
Доплеровские параметры спектра
Смотрите doppler страница с описанием для соответствующих Доплеровских структур спектра для описаний параметров и их значения.
Советы для конфигурирования канала возражают, чтобы настроить процесс фильтрации:
Если ваши данные разделены в серию векторов (что вы обрабатываете в цикле, например), можно вызвать объект канала многократно (в каждой итерации в цикле). Информация состояния канала обновляется и сохранена после каждого вызова. Выход канала не важен тому, как данные разделены (длина вектора).
Если хотят, чтобы канал выход был повторяем, выбрал опцию seed для RandomStream свойство объекта канала. Чтобы повторить выход, вызовите reset возразите функции, чтобы сбросить и внутренние фильтры и внутренний генератор случайных чисел.
Если вы хотите смоделировать с перерывами передаваемые данные, установите FadingTechnique свойство к 'Sum of sinusoids' и InitialTimeSource свойство к 'Input port' для объекта канала. При вызове объекта задайте время начала каждого вектора данных / система координат, которая будет обработана каналом через вход.
Если вы хотите нормировать процесс исчезновения так, чтобы ожидаемое значение общей степени усилений пути равнялось 1 (канал не вносит дополнительное усиление степени или потерю), установите NormalizePathGains свойство канала возражает против true.
После того, как вы создали объект канала как описано в Определении Исчезающего Канала, можно вызвать объект передать сигнал через канал. Обеспечьте сигнал как входной параметр к объекту канала. В конце операции фильтрации объект канала сохраняет свое состояние так, чтобы можно было узнать итоговые усиления пути или общее количество выборок, которые канал обработал путем вызова функции объекта info с объектом как входной параметр.
Для примера, который иллюстрирует базовый синтаксис и задержание состояния, смотрите Степень Увядшего Сигнала.
Чтобы визуализировать характеристики канала, установите Visualization свойство к 'Impulse response', 'Frequency response', или 'Doppler spectrum'. Для получения дополнительной информации смотрите Визуализацию Канала.
Этот пример показывает вам, как визуализировать импульсную характеристику канала.
Создайте объект канала
При создании объекта канала используйте пары "имя-значение", чтобы установить Visualization свойство
к 'Impulse response'.
rayChan = comm.RayleighChannel('SampleRate',100000,'MaximumDopplerShift',130,... 'PathDelays',[0 1.5e-5 3.2e-5],'AveragePathGains',[0, -3, -3],... 'Visualization','Impulse response');
Сгенерируйте немного потока и создайте объект модулятора. Модулируйте поток битов и передайте
модулируемые DBPSK сигнализируют через канал путем вызова объекта канала.
tx = randi([0 1],500,1); dbspkMod = comm.DBPSKModulator; dpskSig = dbspkMod(tx); y = rayChan(dpskSig);

Импульсная характеристика построена, когда объект называется.
Эти примеры использование, исчезающее каналы:
Этот пример строит степень увядшего сигнала по сравнению с демонстрационным номером. Это иллюстрирует синтаксис создания и вызова comm.RayleighChannel исчезающий объект канала и задержание состояния объекта канала.
rayChan = comm.RayleighChannel('SampleRate',10000,'MaximumDopplerShift',100); sig = j*ones(2000,1); % Signal out = rayChan(sig); % Pass signal through channel. rayChan % Display all properties of the channel object.
rayChan =
comm.RayleighChannel with properties:
SampleRate: 10000
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
Постройте степень увядшего сигнала, по сравнению с демонстрационным номером.
plot(20*log10(abs(out)))

Этот пример создает плоский частотой объект Канала с релеевским замиранием и вызывает его, чтобы обработать сигнал DBPSK, состоящий из одного вектора. Частота ошибок по битам вычисляется для различных значений отношения сигнал-шум. Исчезающий фильтр канала применяется перед AWGN. Это - рекомендуемая последовательность, чтобы использовать, когда вы комбинируете исчезновение с AWGN.
Создайте Канал с релеевским замиранием, модулятор и объекты демодулятора
chan = comm.RayleighChannel('SampleRate',1e4,'MaximumDopplerShift',100);
Создайте модулятор DBPSK и объекты демодулятора с набором порядка модуляции к 2. Сгенерируйте модулируемые данные DBPSK и передайте их через канал.
M = 2; % DBPSK modulation order tx = randi([0 M-1],50000,1); % Generate a random bit stream mod = comm.DBPSKModulator; demod = comm.DBPSKDemodulator; dpskSig = mod(tx); fadedSig = chan(dpskSig); % Apply the channel effects
Создайте объект канала AWGN и объект калькулятора коэффициента ошибок.
awgnChan = comm.AWGNChannel('NoiseMethod', 'Signal to noise ratio (SNR)'); errorCalc = comm.ErrorRate;
Вычислите коэффициент ошибок для различных значений ОСШ.
SNR = 0:2:20; % Range of SNR values, in dB. numSNR = length(SNR); berVec = zeros(3, numSNR); % Preallocate a vector for BER results for n = 1:numSNR awgnChan.SNR = SNR(n); rxSig = awgnChan(fadedSig); % Add Gaussian noise rx = demod(rxSig); % Demodulate reset(errorCalc) berVec(:,n) = errorCalc(tx,rx); % Compute error rate. end BER = berVec(1,:);
Вычислите теоретические результаты эффективности для сравнения.
BERtheory = berfading(SNR,'dpsk',M,1);Постройте результаты BER.
semilogy(SNR,BERtheory,'b-',SNR,BER,'r*'); legend('Theoretical BER','Empirical BER'); xlabel('SNR (dB)'); ylabel('BER'); title('Binary DPSK over Rayleigh Fading Channel');

Значение свойства ChannelFilterDelay объекта канала является количеством отсчетов, которым выход канала изолирует вход. Если вы сравниваете наборы входных и выходных данных непосредственно, необходимо принять задержку во внимание при помощи соответствующего усечения или дополнения операций.
Пример иллюстрирует путь с учетом задержки прежде, чем вычислить немного коэффициента ошибок.
Создайте модулятор DBPSK и объекты демодулятора с набором порядка модуляции к 2. Сгенерируйте модулируемые данные DBPSK и передайте их через канал.
bitRate = 50000;
M = 2; % DQPSK modulation order
mod = comm.DBPSKModulator;
demod = comm.DBPSKDemodulator;
Создайте объект Канала с релеевским замиранием.
rayChan = comm.RayleighChannel('SampleRate',bitRate,'MaximumDopplerShift',4,... 'PathDelays',[0 0.5/bitRate],'AveragePathGains',[0 -10]); chInfo = info(rayChan); delay = chInfo.ChannelFilterDelay;
Сгенерируйте случайные данные о потоке битов. Модулируйте данные, передайте их через исчезающий канал и демодулируйте их.
tx = randi([0 M-1],50000,1); dpskSig = mod(tx); fadedSig = rayChan(dpskSig); rx = demod(fadedSig);
Вычислите частоту ошибок по битам, приняв задержку во внимание.
errorCalc = comm.ErrorRate('ReceiveDelay', delay);
berVec = step(errorCalc,tx,rx);
ber = berVec(1)ber = 0.0147
num = berVec(2)
num = 737
Этот пример пропускает входные данные через Канал с релеевским замиранием в for цикл. Это использует небольшие наборы данных от последовательных итераций, чтобы создать анимируемый эффект. Канал с релеевским замиранием имеет два дискретных крупнейших пути. Для получения информации о пропущении данных через канал многократно при поддержании непрерывности от одного вызова до следующего, смотрите, Конфигурируют Объекты Канала На основе Потребностей Симуляции.
Настройте параметры. Задайте немного уровня 50e3 Гц и количество итерации цикла 125. Создайте модулятор QPSK и объекты Канала с релеевским замиранием.
bitRate = 50000; % Data rate is 50 kb/s numTrials = 125; % Number of iterations of loop M = 4; % QPSK modulation order qpskMod = comm.QPSKModulator; rayChan = comm.RayleighChannel('SampleRate',bitRate,'MaximumDopplerShift',4,'PathDelays',[0 2e-5],'AveragePathGains',[0 -9]);
Инициализируйте график рассеивания.
scatterPlot = comm.ConstellationDiagram;
Примените канал в цикле, обеспечив непрерывность. Отобразите на графике только текущие данные в каждой итерации.
for n = 1:numTrials tx = randi([0 M-1],500,1); % Generate random bit stream pskSig = qpskMod(tx); % PSK modulate signal fadedSig = rayChan(pskSig); % Apply channel effects % Plot the new data from this iteration. update(scatterPlot,fadedSig); end

Как правило, усиление пути в исчезающем канале изменяется незначительно в течение 1/(100fd) секунды, где fd максимальный эффект Доплера. Поскольку этот период соответствует очень большому количеству битов во многих современных технологиях беспроводной передачи данных, оценивание эффективности в статистически значительной области значений исчезновения канала требует симуляции предельно большого объема данных. Этот пример иллюстрирует квазистатический подход моделирования канала к сбору статистически значительного количества ошибок. Квазистатическое моделирование канала обеспечивает более послушный подход, который можно реализовать использование этих шагов:
Сгенерируйте случайную реализацию канала с помощью максимального эффекта Доплера 0.
Процесс некоторое большое количество битов.
Вычислите статистику ошибок.
Повторите эти шаги много раз, чтобы произвести распределение показателя производительности.
Создайте модулятор и системные объекты демодулятора с порядком модуляции 4.
M = 4; dpskMod = comm.DPSKModulator('ModulationOrder',M); dpskDemod = comm.DPSKDemodulator('ModulationOrder',M); numBits = 10000; % Each trial uses 10000 bits numTrials = 20; % Number of BER computations
Как правило, numTrials было бы большое количество, чтобы получить точную оценку вероятностей отключения электричества или пакетного коэффициента ошибок. Используйте 20 здесь только, чтобы сделать пример запущенным более быстро.
Создайте объект канала Rician и обнулите максимальный эффект Доплера.
ricianChan = comm.RicianChannel('KFactor',3,'MaximumDopplerShift',0);
В for цикл, сгенерируйте случайный поток битов, DPSK модулируют сигнал, пропускают модулируемый сигнал через исчезновение Rician и каналы AWGN, и демодулируют увядший сигнал. Для расчета коэффициента ошибок символа на каждом пакете проигнорируйте первую выборку из-за условия начальной буквы DPSK.
nErrors = zeros(1,numTrials); for n = 1:numTrials tx = randi([0 M-1],numBits,1); % Generate random bit stream dpskSig = dpskMod(tx); % DPSK modulate signal fadedSig = ricianChan(dpskSig); % Apply channel effects rxSig = awgn(fadedSig,15,'measured'); % Add Gaussian noise rx = dpskDemod(rxSig); % Demodulate nErrors(n) = symerr(tx(2:end),rx(2:end)); % Symbol error computation, beginning with sample index 2 end
После for концы цикла, отображение список ошибки символа рассчитывает в векторном nErrors и расчет пакетного коэффициента ошибок. Запуститесь, чтобы запуститься, результаты варьируются из-за случайности в примере.
nErrors
nErrors = 1×20
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
per = mean(nErrors > 0) % Proportion of packets that had errorsper = 0.0500
Как пример, чтобы показать, как квазистатический подход моделирования канала может сохранить расчет, рассмотрите беспроводную локальную сеть (LAN), в которой несущая частота составляет 2,4 ГГц, мобильная скорость составляет 1 м/с, и битрейт составляет 10 Мбит/с. Следующее выражение показывает, что канал изменяет незначительно более чем 12 500 битов:
Традиционный подход Монте-Карло для вычисления коэффициента ошибок этой системы повлек бы за собой симуляцию тысячи времен, в общей сложности десятки миллионов битов. В отличие от этого, квазистатический подход моделирования канала симулировал бы несколько пакетов в каждом приблизительно 100 местах, чтобы достигнуть пространственного распределения коэффициентов ошибок. От этого распределения можно было определить, например, насколько надежный линия связи для случайного местоположения во внутреннем пробеле. Если бы каждая симуляция содержит 5 000 битов, 100 симуляций обработали бы полмиллиона битов всего. Это - существенно меньше битов по сравнению с традиционным подходом Монте-Карло.