Модель Gaussian соответствует peaks и дана
где a является амплитудой, b является центроидом (местоположение), c связан с пиковой шириной, n является количеством peaks, чтобы соответствовать, и 1 ≤ n ≤ 8.
С гауссовым peaks сталкиваются во многих областях науки и разработки. Например, Гауссов peaks может описать спектры эмиссии линии и химическое испытание концентрации.
Откройте приложение Curve Fitting путем ввода cftool. В качестве альтернативы нажмите Curve Fitting на вкладке Apps.
В приложении Curve Fitting выберите данные о кривой (X data и Y data, или только Y data против индекса).
Приложение Curve Fitting создает подгонку кривой по умолчанию, Polynomial.
Измените тип модели от Polynomial к Gaussian.
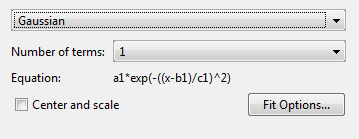
Можно задать следующие опции:
Выберите количество терминов: 1 к 8.
Посмотрите в панели Results, чтобы видеть термины модели, значения коэффициентов и статистику качества подгонки.
(Необязательно) Нажмите Fit Options, чтобы задать содействующие начальные значения и ограничительные границы, или изменить настройки алгоритма.
Тулбокс вычисляет оптимизированные стартовые точки для моделей Gaussian, на основе текущего набора данных. Можно заменить стартовые точки и задать собственные значения в Подходящем Окне параметров.
Gaussians имеют параметр ширины c1 ограниченный с нижней границей 0. Нижними границами по умолчанию для большинства моделей библиотеки является -Inf, который указывает, что коэффициенты неограничены.
Для получения дополнительной информации о настройках см. Опции Подгонки Определения и Оптимизированные Начальные точки.
В этом примере показано, как использовать fit функция, чтобы подбирать модель Gaussian к данным.
Модель библиотеки Gaussian является входным параметром к fit и fittype функции. Задайте тип модели gauss сопровождаемый количеством терминов, например, 'gauss1' через 'gauss8' .
Соответствуйте 2D термину гауссова модель
Загрузите некоторые данные и подбирайте модель Gaussian 2D термина.
[x,y] = titanium;
f = fit(x.',y.','gauss2')f =
General model Gauss2:
f(x) = a1*exp(-((x-b1)/c1)^2) + a2*exp(-((x-b2)/c2)^2)
Coefficients (with 95% confidence bounds):
a1 = 1.47 (1.426, 1.515)
b1 = 897.7 (897, 898.3)
c1 = 27.08 (26.08, 28.08)
a2 = 0.6994 (0.6821, 0.7167)
b2 = 810.8 (790, 831.7)
c2 = 592.9 (500.1, 685.7)
plot(f,x,y)

fit | fittype | fitoptions