Совет
Чтобы обучить нейронную сеть для глубокого обучения, использовать trainNetwork.
Эта тема представляет часть типичного многоуровневого мелкого сетевого рабочего процесса. Для получения дополнительной информации и другие шаги, смотрите Многоуровневые Мелкие Нейронные сети и Обучение Обратной связи.
Когда сетевые веса и смещения инициализируются, сеть готова к обучению. Многоуровневая сеть прямого распространения может быть обучена приближению функций (нелинейная регрессия) или распознавание образов. Учебный процесс требует набора примеров соответствующего сетевого поведения — сеть вводит p и целевые выходные параметры t.
Процесс обучения нейронной сети включает настройку значений весов и смещений сети, чтобы оптимизировать производительность сети, как задано функцией производительности сети net.performFcn. Функция эффективности по умолчанию для сетей прямого распространения является среднеквадратичной погрешностью mse— средняя квадратичная невязка между сетевыми выходными параметрами a и целевые выходные параметры t. Это определяется следующим образом:
(Отдельные квадратичные невязки могут также быть взвешены. Смотрите Обучают Нейронные сети с Весами ошибок.) Существует два различных пути, которыми может быть реализовано обучение: инкрементный режим и пакетный режим. В инкрементном режиме вычисляется градиент, и веса обновляются после того, как каждый вход применяется к сети. В пакетном режиме все входные параметры в наборе обучающих данных применяются к сети, прежде чем веса будут обновлены. Эта тема описывает обучение пакетного режима с train команда. Инкрементное обучение с adapt команда обсуждена в Инкрементном Обучении с, адаптируются. Для большинства проблем, при использовании программного обеспечения Deep Learning Toolbox™, пакетное обучение значительно быстрее и производит меньшие ошибки, чем инкрементное обучение.
Для учебных многоуровневых сетей прямого распространения любой стандартный числовой алгоритм оптимизации может использоваться, чтобы оптимизировать функцию эффективности, но существует несколько ключевых единиц, которые показали превосходную эффективность для обучения нейронной сети. Эти методы оптимизации используют или градиент производительности сети относительно сетевых весов или якобиан сетевых ошибок относительно весов.
Градиент и якобиан вычисляются с помощью метода, названного алгоритмом обратного распространения, который включает расчеты выполнения назад через сеть. Расчет обратной связи выведен, использовав цепочечное правило исчисления и описан в Главах 11 (для градиента) и 12 (для якобиана) [HDB96].
Как рисунок того, как обучение работает, рассмотрите самый простой алгоритм оптимизации — градиентный спуск. Это обновляет сетевые веса и смещения в направлении, в котором функция эффективности уменьшается наиболее быстро, отрицание градиента. Одна итерация этого алгоритма может быть записана как
где x, k является вектором из текущих весов и смещений, g k, является текущим градиентом, и αk является скоростью обучения. Это уравнение выполнено с помощью итераций, пока сеть не сходится.
Список алгоритмов настройки, которые доступны в программном обеспечении Deep Learning Toolbox и том градиенте использования - или Основанные на якобиане методы, показывают в следующей таблице.
Для подробного описания нескольких из этих методов см. также Хейгана, M.T., Х.Б. Демут, и М.Х. Биль, Neural Network Design, Бостон, MA: PWS Publishing, 1996, Главы 11 и 12.
Функция | Алгоритм |
|---|---|
Levenberg-Marquardt | |
Байесова регуляризация | |
Квазиньютон BFGS | |
Устойчивая обратная связь | |
Масштабированный метод сопряженных градиентов | |
Метод сопряженных градиентов с Перезапусками Powell/Beale | |
Метод сопряженных градиентов Флетчера-Пауэлла | |
Метод сопряженных градиентов Полака-Рибиера | |
Один секанс шага | |
Переменный градиентный спуск скорости обучения | |
Градиентный спуск с импульсом | |
Градиентный спуск |
Самая быстрая учебная функция обычно trainlm, и это - учебная функция по умолчанию для feedforwardnet. Приближенный метод ньютона, trainbfg, также довольно быстро. Оба из этих методов имеют тенденцию быть менее эффективными для больших сетей (с тысячами весов), поскольку они требуют большей памяти и больше времени вычисления для этих случаев. Кроме того, trainlm выполняет лучше на подборе кривой функции (нелинейная регрессия) проблемы, чем на проблемах распознавания образов.
При обучении больших сетей, и при обучении сетей распознавания образов, trainscg и trainrp хороший выбор. Их требования к памяти относительно малы, и все же они намного быстрее, чем стандартные алгоритмы градиентного спуска.
Смотрите Выбирают Multilayer Neural Network Training Function для полного сравнения эффективности алгоритмов настройки, показанных в приведенной выше таблице.
Как примечание по терминологии, термин “обратная связь” иногда используется, чтобы обратиться в частности к алгоритму градиентного спуска, когда применился к обучению нейронной сети. Та терминология не используется здесь, поскольку процесс вычисления градиента и якобиана путем выполнения вычислений назад через сеть применяется во всех учебных упомянутых выше функциях. Это более ясно использовать имя определенного алгоритма оптимизации, который используется, вместо того, чтобы использовать термин одна только обратная связь.
Кроме того, многоуровневая сеть иногда упоминается как сеть обратной связи. Однако метод обратной связи, который является использованными для расчета градиентами и Якобианами в многоуровневой сети, может также быть применен ко многим различным сетевым архитектурам. На самом деле градиенты и Якобианы для любой сети, которая имеет дифференцируемые передаточные функции, функции веса и сетевые функции ввода, могут быть вычислены с помощью программного обеспечения Deep Learning Toolbox посредством процесса обратной связи. Можно даже создать собственные сети и затем обучить их использующий любую из учебных функций в приведенной выше таблице. Градиенты и Якобианы будут автоматически вычислены для вас.
Чтобы проиллюстрировать учебный процесс, выполните следующие команды:
load bodyfat_dataset
net = feedforwardnet(20);
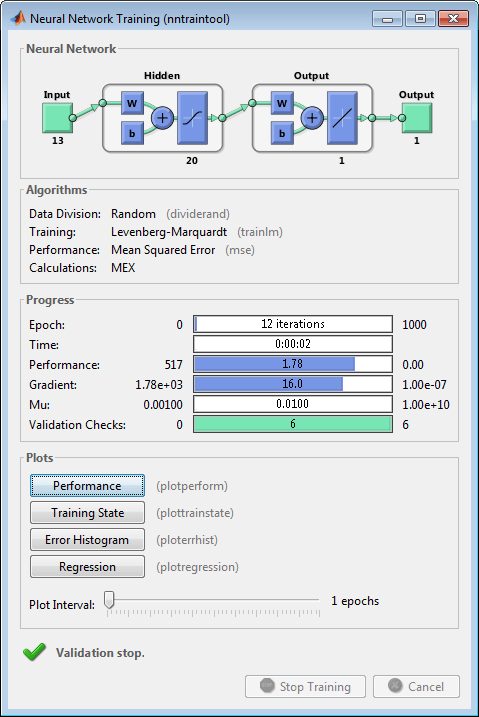
[net,tr] = train(net,bodyfatInputs,bodyfatTargets);Заметьте, что вы не должны были выходить configure команда, потому что конфигурация реализована автоматически train функция. Учебное окно появится во время обучения как показано в следующем рисунке. (Если вы не хотите отображать это окно во время обучения, можно установить параметр net.trainParam.showWindow к false. Если вы хотите учебную информацию, отображенную в командной строке, можно установить параметр net.trainParam.showCommandLine к true.)
Это окно показывает, что данные были разделены с помощью dividerand функция и Levenberg-Marquardt (trainlm) метод обучения использовался с функцией эффективности среднеквадратичной погрешности. Вспомните, что это настройки по умолчанию для feedforwardnet.
Во время обучения прогресс постоянно обновляется в учебном окне. Из большей части интереса эффективность, величина градиента эффективности и количества проверок валидации. Величина градиента и количество проверок валидации используются, чтобы отключить обучение. Градиент станет очень маленьким, когда обучение достигает минимума эффективности. Если величина градиента будет меньше 1e-5, обучение остановится. Этот предел может быть настроен путем установки параметра net.trainParam.min_grad. Количество проверок валидации представляет количество последовательных итераций, которые эффективности валидации не удается уменьшить. Если этот номер достигнет 6 (значение по умолчанию), обучение остановится. В этом запуске вы видите, что обучение действительно останавливалось из-за количества проверок валидации. Можно изменить этот критерий путем установки параметра net.trainParam.max_fail. (Обратите внимание на то, что ваши результаты могут отличаться, чем показанные в следующем рисунке из-за случайной установки начальных весов и смещений.)
Существуют другие критерии, которые могут использоваться, чтобы остановить сетевое обучение. Они перечислены в следующей таблице.
Параметр | Критерий остановки |
|---|---|
min_grad | Минимальная величина градиента |
max_fail | Максимальное количество увеличений валидации |
time | Максимальное учебное время |
goal | Минимальное значение эффективности |
epochs | Максимальное количество учебных эпох (итерации) |
Обучение также остановится, если вы нажмете кнопку Stop Training в учебном окне. Вы можете хотеть сделать это, если функции эффективности не удается уменьшиться значительно по многим итерациям. Всегда возможно продолжить обучение путем переиздания train команда, показанная выше. Это продолжит обучать сеть от завершения предыдущего запуска.
Из учебного окна можно получить доступ к четырем графикам: эффективность, учебное состояние, ошибочная гистограмма и регрессия. График эффективности показывает значение функции эффективности по сравнению с номером итерации. Это строит обучение, валидацию и проведение испытаний. Учебный график состояния показывает прогресс других учебных переменных, таких как величина градиента, количество проверок валидации, и т.д. Ошибочный график гистограммы показывает распределение сетевых ошибок. График регрессии показывает регрессию между сетевыми выходными параметрами и сетевыми целями. Можно использовать гистограмму и графики регрессии, чтобы подтвердить производительность сети, как обсужден в, Анализируют Мелкую Эффективность Нейронной сети После Обучения.
После того, как сеть обучена и подтверждена, сетевой объект может использоваться, чтобы вычислить сетевой ответ на любой вход. Например, если вы хотите найти сетевой ответ на пятый входной вектор в наборе данных создания, можно использовать следующее
a = net(bodyfatInputs(:,5))
a = 27.3740
Если вы пробуете эту команду, ваш выход может отличаться, в зависимости от состояния вашего генератора случайных чисел, когда сеть была инициализирована. Ниже, сетевой объект называется, чтобы вычислить выходные параметры для параллельного набора всех входных векторов в наборе данных жировой прослойки. Это - форма пакетного режима симуляции, в которой все входные векторы помещаются в одну матрицу. Это намного более эффективно, чем представление векторов по одному.
a = net(bodyfatInputs);
Каждый раз нейронная сеть обучена, может привести к различному решению из-за различного начального веса и сместить значения и различные деления данных в обучение, валидацию и наборы тестов. В результате различные нейронные сети, обученные на той же проблеме, могут дать различные выходные параметры для того же входа. Чтобы гарантировать, что нейронная сеть хорошей точности была найдена, переобучайтесь несколько раз.
Существует несколько других методов для того, чтобы улучшить начальные решения, если более высокая точность желаема. Для получения дополнительной информации смотрите, Улучшают Мелкое Обобщение Нейронной сети и Стараются не Сверхсоответствовать.