Библиотека Matrices и Linear Algebra обеспечивает три крупных подбиблиотеки, содержащие блоки в линейной алгебре; Решатели Линейной системы, Матричные Факторизации и Обратные матрицы. Четвертая библиотека, Матричные операции, обеспечивает другие существенные блоки для работы с матрицами.
Библиотека Linear System Solvers обеспечивает следующие блоки для решения системы AX линейных уравнений = B:
Некоторые блоки предлагают особые сильные места для определенных классов проблем. Например, блок Cholesky Solver адаптируется к квадратной Эрмитовой положительной определенной матрице А, тогда как блок Backward Substitution подходит для верхней треугольной матрицы A.
В следующей ex_lusolver_tut модели блок LU Solver решает уравнение Ax = b, где
и находит, что x векторный [-2 0 1]'.
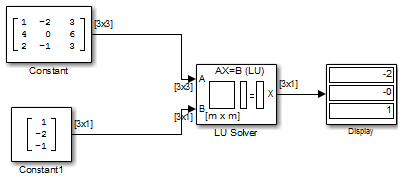
Можно проверить решение при помощи блока Matrix Multiply, чтобы выполнить умножение Ax, как показано в следующей ex_matrixmultiply_tut1 модели.

Библиотека Matrix Factorizations обеспечивает следующие блоки для факторинга различных видов матриц:
Некоторые блоки предлагают особые сильные места для определенных классов проблем. Например, блок Cholesky Factorization подходит для факторинга Эрмитовой положительной определенной матрицы на треугольные компоненты, тогда как QR-факторизация подходит для факторинга прямоугольной матрицы на унитарные и верхние треугольные компоненты.
В следующей ex_lufactorization_tut модели, блоковые факторы LU-факторизации матричное AP в верхние и нижние треугольные подматрицы U и L, где AP является строкой, эквивалентной, чтобы ввести матрицу А, где
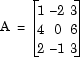
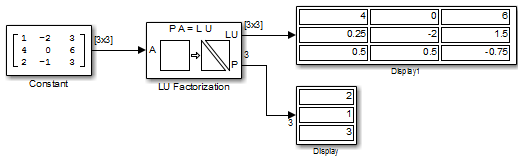
Более низкий выход LU-факторизации, P, вектор индекса сочетания, который указывает, что учтенный матричный Ap сгенерирован от путем обмена первыми и вторыми строками.
Верхний выход LU-факторизации, LU, составная матрица, содержащая два фактора субматрицы, U и L, LU продукта которого равен AP.
Можно проверять что LU = Ap с блоком Matrix Multiply, как показано в следующей ex_matrixmultiply_tut2 модели.
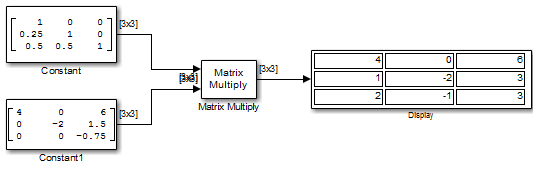
Библиотека Matrix Inverses обеспечивает следующие блоки для инвертирования различных видов матриц:
В следующей ex_luinverse_tut модели блок LU Inverse вычисляет инверсию входной матрицы А, где
и затем формирует продукт A-1A, который дает к единичной матрице порядка 3, как ожидалось.
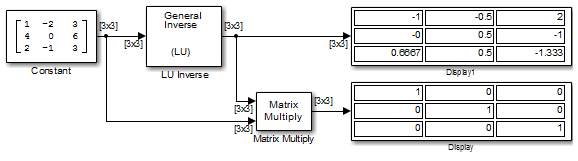
Как показано выше, вычисленная инверсия