Документация

Начальная загрузка от инвертированных кривых рынка

Следующий двум примерам демонстрирует поведение начальной загрузки с инвертированными кривыми рынка CDS, то есть, рыночными котировками с более высокими распространениями для краткосрочных контрактов CDS. Первый пример обычно обрабатывается cdsbootstrap:

Settle = '17-Jul-2009';  % valuation date for the CDS
MarketDates = datenum({'20-Sep-10','20-Sep-11','20-Sep-12','20-Sep-14',...
'20-Sep-16'});

ZeroDates = datenum({'17-Jan-10','17-Jul-10','17-Jul-11','17-Jul-12',...
'17-Jul-13','17-Jul-14'});
ZeroRates = [1.35 1.43 1.9 2.47 2.936 3.311]'/100;
ZeroData = [ZeroDates ZeroRates];

MarketSpreadsInv1 = [750 650 550 500 450]';
MarketDataInv1 = [MarketDates MarketSpreadsInv1];
[ProbDataInv1,HazDataInv1] = cdsbootstrap(ZeroData,MarketDataInv1,Settle)

ProbDataInv1 =

   1.0e+05 *

    7.3440    0.0000
    7.3477    0.0000
    7.3513    0.0000
    7.3586    0.0000
    7.3659    0.0000


HazDataInv1 =

   1.0e+05 *

    7.3440    0.0000
    7.3477    0.0000
    7.3513    0.0000
    7.3586    0.0000
    7.3659    0.0000

Во втором примере, cdsbootstrap генерирует предупреждение:

MarketSpreadsInv2 = [800 550 400 250 100]';
MarketDataInv2 = [MarketDates MarketSpreadsInv2];

[ProbDataInv2,HazDataInv2] = cdsbootstrap(ZeroData,MarketDataInv2,Settle);

Warning: Found non-monotone default probabilities (negative hazard rates)

Немонотонность загрузилась, кривая вероятности подразумевает отрицательные вероятности по умолчанию и отрицательные показатели риска для определенных временных интервалов. Экстремальное состояние рынка может привести к этим типам ситуаций. В этих случаях необходимо оценить надежность и полноценность загруженных результатов.

Следующий график иллюстрирует эти загруженные кривые вероятности. Кривые являются вогнутыми, означая, что крайняя вероятность по умолчанию уменьшается со временем. Этот результат сопоставим с информацией о рынке, которая указывает на более высокий кредитный риск в ближайшей перспективе. Вторая загруженная кривая является немонотонностью, как обозначено предупреждением.

ProbTimes = yearfrac(Settle, MarketDates);
figure
plot([0; ProbTimes],[0; ProbDataInv1(:,2)])
hold on
plot([0; ProbTimes],[0; ProbDataInv2(:,2)],'--')
hold off
grid on
axis([0 ProbTimes(end,1) 0 ProbDataInv1(end,2)])
xlabel('Time (years)')
ylabel('Cumulative Default Probability')
title('Probability Curves for Inverted Spread Curves')
legend('1st instance','2nd instance','location','SouthEast')

Получившийся график

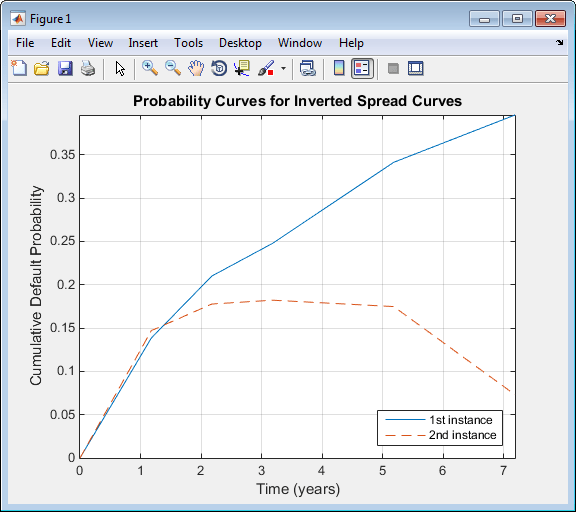
Также в соответствии с предыдущим графиком, показатели риска для этих загруженных кривых уменьшаются, потому что краткосрочный риск выше. Некоторые загруженные параметры во второй кривой отрицательны, как обозначено предупреждением.

HazTimes = yearfrac(Settle, MarketDates);
figure
stairs([0; HazTimes(1:end-1,1); HazTimes(end,1)+1],...
   [HazDataInv1(:,2);HazDataInv1(end,2)])
hold on
stairs([0; HazTimes(1:end-1,1); HazTimes(end,1)+1],...
   [HazDataInv2(:,2);HazDataInv2(end,2)],'--')
hold off
grid on
xlabel('Time (years)')
ylabel('Hazard Rate')
title('Hazard Rates for Inverted Spread Curves')
legend('1st instance','2nd instance','location','NorthEast')

Получившийся график показывает показатели риска для обеих загруженных кривых:

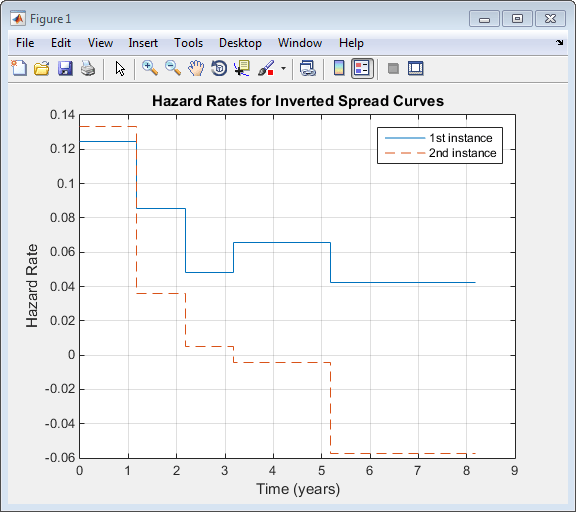
Для дальнейшего обсуждения инвертированных кривых и их отношения к арбитражу, смотрите О'Кэйна и Тернбулла, 2003 (Кредитные деривативы).

Смотрите также

cdsbootstrap | cdsprice | cdsspread | cdsrpv01

Похожие темы

• Первые к значению по умолчанию подкачки (Financial Instruments Toolbox)
• Опция кредитного дефолтного свопа (Financial Instruments Toolbox)
• Кредитный риск контрагента и CVA (Financial Instruments Toolbox)