Хеджирование является инвестициями, чтобы снизить риск неблагоприятной динамики цен в активе. Financial Instruments Toolbox™ предлагает две функции для оценки фундаментального компромисса хеджирования, hedgeopt и hedgeslf.
Первая функция, hedgeopt, решает самую общую проблему хеджирования. Это выделяет оптимальную преграду, чтобы удовлетворить любому из двух голов:
Минимизируйте стоимость хеджирования портфеля, учитывая набор целевой чувствительности.
Минимизируйте чувствительность портфеля для данного набора максимальных целевых затрат.
hedgeopt позволяет инвесторам изменять выделения портфеля среди инструментов согласно любой из целей. Проблема снята как ограниченная проблема линейного метода наименьших квадратов. Для получения дополнительной информации о hedgeopt, смотрите Хеджирование с hedgeopt.
Вторая функция, hedgeslf, попытки выделить самофинансирующуюся преграду среди портфеля инструментов. В частности, hedgeslf попытки обеспечить постоянную стоимость портфеля, сопоставимую с уменьшаемой чувствительностью портфеля (то есть, перебалансированный портфель застрахован против перемещений рынка и самый близкий к тому, чтобы быть самофинансирующимся). Если hedgeslf не может найти самофинансирующуюся преграду, она восстанавливает равновесие портфеля, чтобы минимизировать полную чувствительность портфеля. Для получения дополнительной информации о hedgeslf, смотрите Самофинансирующиеся Преграды с hedgeslf.
Примеры в этом разделе рассматривают дельту, гамму и vega меры по чувствительности. В этом тулбоксе, когда вы работаете с производными процентной ставки, дельта является ценовой мерой по чувствительности, переключает прямую кривую доходности на нижний регистр, гамма является мерой по чувствительности дельты, переключает прямую кривую доходности на нижний регистр, и vega является ценовой мерой по чувствительности, переключает процесс энергозависимости на нижний регистр. Смотрите bdtsens или hjmsens для получения дополнительной информации о расчете чувствительности для производных процентной ставки.
Для акции экзотические опции базовый инструмент является курсом акций вместо прямой кривой доходности. Так, дельта теперь представляет ценовую меру по чувствительности, переключает курс акций на нижний регистр, гамма является мерой по чувствительности дельты, переключает курс акций на нижний регистр, и vega является ценовой мерой по чувствительности, переключает энергозависимость на нижний регистр запаса. Смотрите crrsens, eqpsens, ittsens, или sttsens для получения дополнительной информации о расчете чувствительности для производных акции.
Для примеров, показывающих расчет чувствительности для основанных на процентной ставке производных, смотрите Вычислительную Инструментальную Чувствительность. Аналогично, для примеров, показывающих расчет чувствительности для акции экзотические опции, смотрите Вычислительную Инструментальную Чувствительность Акции.
Примечание
Дельта, гамма и vega чувствительность, которую вычисляет тулбокс, являются долларовой чувствительностью.
hedgeoptПримечание
Числовые результаты в этом разделе отображены в MATLAB® формат банка. Несмотря на то, что вычисления выполняются в двойной точности с плавающей точкой, только два десятичных разряда отображены.
Чтобы проиллюстрировать средство хеджирования, считайте портфель HJMInstSet полученный из файла в качестве примера deriv.mat. Портфель состоит из восьми инструментов: две связи, одна опция связи, одно примечание с фиксированной процентной ставкой, одно долговое обязательство с плавающей ставкой, одно дно, один пол и одна подкачка.
И функции хеджирования требуют некоторых общих входных параметров, включая текущие активы портфеля (выделения) и матрица инструментальной чувствительности. Чтобы создать эти входные параметры, загрузите портфель в качестве примера в память
load deriv.mat;
вычислите цену и чувствительность
[Delta, Gamma, Vega, Price] = hjmsens(HJMTree, HJMInstSet);
Warning: Not all cash flows are aligned with the tree. Result will be approximated.
и извлеките текущие активы портфеля.
Holdings = instget(HJMInstSet, 'FieldName', 'Quantity');
Поскольку удобство помещает дельту, гамму и vega меры по чувствительности в матрицу чувствительности.
Sensitivities = [Delta Gamma Vega];
Каждая строка Sensitivities матрица сопоставлена с различным инструментом в портфеле и каждым столбцом с различной мерой по чувствительности.
Обобщать информацию о портфеле
disp([Price Holdings Sensitivities])
98.72 100.00 -272.65 1029.90 0.00 97.53 50.00 -347.43 1622.69 -0.04 0.05 -50.00 -8.08 643.40 34.07 98.72 80.00 -272.65 1029.90 0.00 100.55 8.00 -1.04 3.31 0 6.28 30.00 294.97 6852.56 93.69 0.05 40.00 -47.16 8459.99 93.69 3.69 10.00 -282.05 1059.68 0.00
Первый столбец выше является долларовой ценой за единицу товара каждого инструмента, вторыми являются активы каждого инструмента (сохраненное количество или количество контрактов), и третьи, четвертые, и пятые колонны являются долларовой дельтой, гаммой и vega чувствительностью, соответственно.
Текущая чувствительность портфеля является взвешенным средним инструментов в портфеле.
TargetSens = Holdings' * Sensitivities
TargetSens =
-61910.22 788946.21 4852.91Проиллюстрировать использование hedgeopt, предположите, что вы хотите обеспечить свой существующий портфель. Первая форма hedgeopt минимизирует стоимость хеджирования портфеля, учитывая набор целевой чувствительности. Если вы хотите обеспечить свою существующую структуру портфеля и воздействие, необходимо смочь сделать так, не тратя денег. Чтобы проверить это, установите целевую чувствительность к текущей чувствительности.
FixedInd = [1 2 3 4 5 6 7 8]; [Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,Holdings, FixedInd, [], [], TargetSens)
Holdings =
100.00
50.00
-50.00
80.00
8.00
30.00
40.00
10.00
Sens =
-61910.22 788946.21 4852.91
Cost =
0
Quantity =
Columns 1 through 6
100.00 50.00 -50.00 80.00 8.00 30.00
Columns 7 through 8
40.00 10.00Структура портфеля и чувствительность неизменны, и стоимость, сопоставленная с выполнением, ничто не нуль. Стоимость задана как изменение в стоимости портфеля. Этот номер не может быть меньше нуля, потому что стоимость изменения баланса задана как неотрицательный номер.
Если Value0 и Value1 представляйте стоимость портфеля до и после изменения баланса, соответственно, нулевая стоимость может также быть проверена путем сравнения стоимости портфеля.
Value0 = Holdings' * Price
Value0 =
23674.62
Value1 = Quantity * Price
Value1 =
23674.62При построении на примере в Поддержании Существующих Выделений предположите, что вы хотите знать, что стоимость достигает полной долларовой чувствительности портфеля [-23000 -3300 3000], при разрешении торговли только в инструментах 2, 3, и 6 (занимание позиций инструментов 1, 4, 5, 7, и 8 зафиксированных). Чтобы найти стоимость, сначала установите целевую долларовую чувствительность портфеля.
TargetSens = [-23000 -3300 3000];
Затем задайте инструменты, которые будут зафиксированы.
FixedInd = [1 4 5 7 8];
Наконец, вызвать hedgeopt
[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,... Holdings, FixedInd, [], [], TargetSens);
и снова исследуйте результаты.
Sens =
-23000.00 -3300.00 3000.00
Cost =
19174.02
Quantity' =
100.00
-141.03
137.26
80.00
8.00
-57.96
40.00
10.00
Повторно вычислите Value1, стоимость портфеля после изменения баланса.
Value1 = Quantity * Price
Value1 =
4500.60
Как ожидалось стоимость, 19 174,02$, является различием между Value0 и Value1, 23 674,62$ — 4 500,60$. Только положения в инструментах 2, 3, и 6 сменились.
Пример в Частично Застрахованном Портфеле иллюстрирует частичную преграду, но возможно самый интересный случай связал стоимость, сопоставленную с полностью застрахованным портфелем (одновременная дельта, гамма и vega нейтралитет). В этом случае установите целевую чувствительность к вектору-строке из 0s и вызова hedgeopt снова. Следующий пример использует данные из Хеджирования с hedgeopt.
TargetSens = [0 0 0]; [Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price, ... Holdings, FixedInd, [], [], TargetSens);
Исследование выходных параметров показывает, что вы получили полностью застрахованный портфель
Sens =
-0.00 -0.00 -0.00
но за счет более чем 20 000$.
Cost =
23055.90
Положения, требуемые достигнуть полностью застрахованного портфеля
Quantity' =
100.00
-182.36
-19.55
80.00
8.00
-32.97
40.00
10.00
приведите к новой стоимости портфеля
Value1 = Quantity * Price
Value1 =
618.72Примеры в Полностью Застрахованном Портфеле иллюстрируют, как использовать hedgeopt определить минимальную стоимость хеджирования портфеля, учитывая набор целевой чувствительности. В этих примерах целевая чувствительность портфеля обработана как ограничения равенства во время процесса оптимизации. Вы говорите hedgeopt какую чувствительность вы хотите, и это говорит вам, чего это будет стоить, чтобы получить ту чувствительность.
Связанная проблема включает чувствительность портфеля минимизации для данного набора максимальных целевых затрат. Для этой цели целевые затраты обработаны как ограничения неравенства во время процесса оптимизации. Вы говорите hedgeopt большинство вы желаете, тратит, чтобы изолировать ваш портфель, и это говорит вам наименьшую чувствительность портфеля, которую можно получить для денег.
Проиллюстрировать это использование hedgeopt, вычислите долларовую чувствительность портфеля вдоль целой границы стоимости. От предыдущих примеров вы знаете, что расходы ничего реплицируют существующий портфель, в то время как расходование 23 055,90$ полностью страхует портфель.
Примите, например, вы готовы потратить целых 50 000$ и хотеть видеть, какая чувствительность портфеля закончится вдоль границы стоимости. Примите, что те же инструменты считаются зафиксированные, и что граница стоимости оценена от 0$ до 50 000$ в шаге 1 000$.
MaxCost = [0:1000:50000];
Теперь вызовите hedgeopt.
[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price, ... Holdings, FixedInd, [], MaxCost);
С этими данными можно построить необходимую стоимость хеджирования по сравнению с доступными фондами (сумма, которую вы готовы потратить),
plot(MaxCost/1000, Cost/1000, 'red'), grid xlabel('Funds Available for Rebalancing ($1000''s)') ylabel('Actual Rebalancing Cost ($1000''s)') title ('Rebalancing Cost Profile')
Изменение баланса профиля стоимости
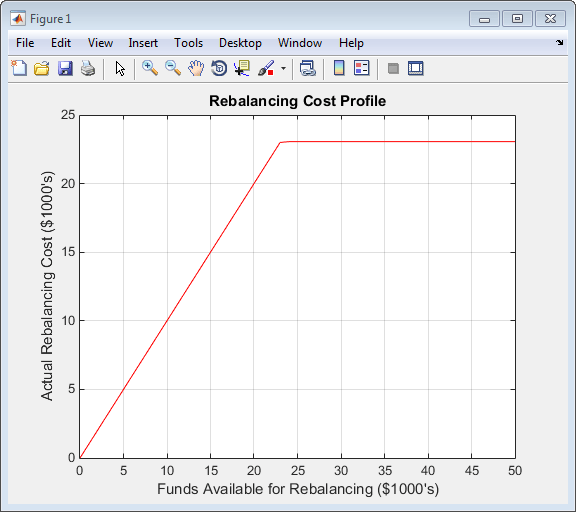
и долларовая чувствительность портфеля по сравнению с доступными фондами.
figure plot(MaxCost/1000, Sens(:,1), '-red') hold('on') plot(MaxCost/1000, Sens(:,2), '-.black') plot(MaxCost/1000, Sens(:,3), '--blue') grid xlabel('Funds Available for Rebalancing ($1000''s)') ylabel('Delta, Gamma, and Vega Portfolio Dollar Sensitivities') title ('Portfolio Sensitivities Profile') legend('Delta', 'Gamma', 'Vega', 0)
Фонды, доступные для изменения баланса
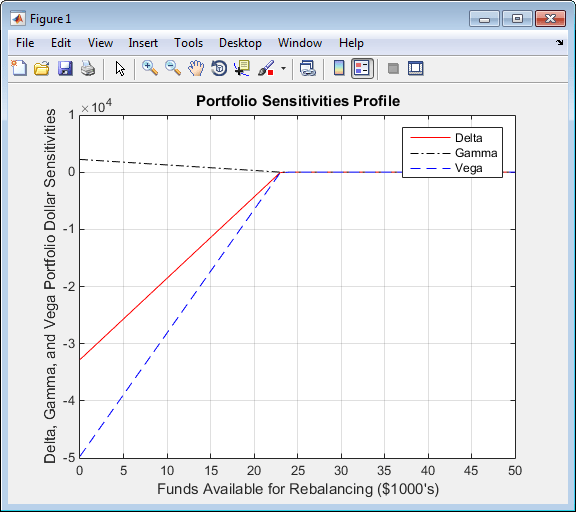
hedgeslfФигуры, Восстанавливающие равновесие Профиля Стоимости и Фондов, Доступных для Изменения баланса, указывают, что нет никакого преимущества, потому что фонды, доступные для хеджирования, превышают 23 055,90$, точка максимального расхода, требуемого получить одновременную дельту, гамму и vega нейтралитет. Можно также найти эту точку дельты, гаммы и vega использования нейтралитета hedgeslf.
[Sens, Value1, Quantity] = hedgeslf(Sensitivities, Price,... Holdings, FixedInd);
Sens =
-0.00
-0.00
-0.00
Value1 =
618.72
Quantity =
100.00
-182.36
-19.55
80.00
8.00
-32.97
40.00
10.00
Подобно hedgeopt, hedgeslf возвращает долларовую чувствительность портфеля и инструментальные количества (перебалансированные активы). Однако напротив, второй выходной параметр hedgeslf значение перебалансированного портфеля, от которого можно вычислить изменение баланса, стоившее вычитанием.
Value0 - Value1
ans =
23055.90
В этом примере портфель является ясно не самофинансирующимся, таким образом, hedgeslf находит самое лучшее решение требуемым получить нулевую чувствительность.
Существует, на самом деле, третий синтаксис вызова, доступный для hedgeopt непосредственно связанный с результатами, показанными выше для hedgeslf. Предположим, вместо того, чтобы непосредственно задать фонды, доступные для изменения баланса (большая часть денег вы готовы потратить), вы хотите просто задать число точек вдоль границы стоимости. Этот вызов hedgeopt производит границу стоимости в 10 равномерно распределенных точках между точкой минимальной стоимости (и потенциально максимальным воздействием) и точкой минимального воздействия (и максимальной стоимости).
[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,... Holdings, FixedInd, 10)
Sens =
-32784.46 2231.83 -49694.33
-29141.74 1983.85 -44172.74
-25499.02 1735.87 -38651.14
-21856.30 1487.89 -33129.55
-18213.59 1239.91 -27607.96
-14570.87 991.93 -22086.37
-10928.15 743.94 -16564.78
-7285.43 495.96 -11043.18
-3642.72 247.98 -5521.59
0.00 -0.00 0.00
Cost =
0.00
2561.77
5123.53
7685.30
10247.07
12808.83
15370.60
17932.37
20494.14
23055.90
Теперь отобразите эти данные на графике.
figure plot(Cost/1000, Sens(:,1), '-red') hold('on') plot(Cost/1000, Sens(:,2), '-.black') plot(Cost/1000, Sens(:,3), '--blue') grid xlabel('Rebalancing Cost ($1000''s)') ylabel('Delta, Gamma, and Vega Portfolio Dollar Sensitivities') title ('Portfolio Sensitivities Profile') legend('Delta', 'Gamma', 'Vega', 0)
Изменение баланса стоимости
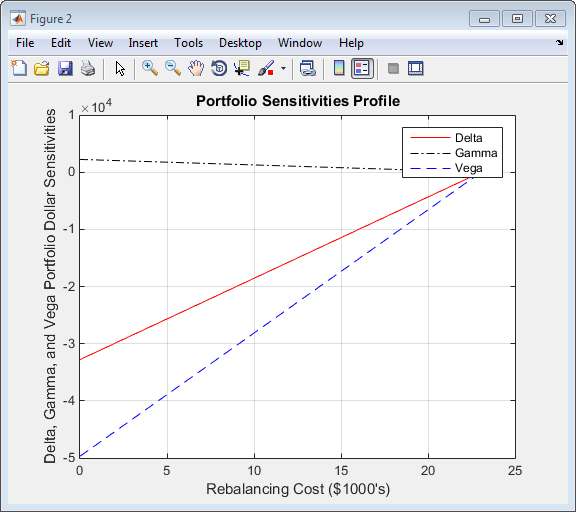
В этой форме вызова, hedgeopt вызовы hedgeslf внутренне определить максимальную стоимость должно было минимизировать чувствительность портфеля (23 055,90$), и равномерно производит границу стоимости между 0$ и 23 055,90$.
Оба hedgeopt и hedgeslf снимите задачу оптимизации в качестве ограниченной проблемы линейного метода наименьших квадратов. В зависимости от инструментов и ограничений, никакая функция, как не гарантируют, будет сходиться к решению. В некоторых случаях пространство задач может быть неограниченными, и дополнительными инструментальными ограничениями равенства или заданными пользователями ограничениями, может быть необходимым для сходимости. Смотрите Хеджирование с Ограниченными Портфелями для получения дополнительной информации.