Графики частотных характеристик линейной модели обеспечивают понимание характеристик динамики модели, включая частоту максимальной чувствительности и запасов устойчивости. Можно использовать графики частотных характеристик, может помочь подтвердить, как хорошо линейная параметрическая модель получает динамику. System Identification Toolbox™ предоставляет несколько возможностей графического вывода.
Графики частотных характеристик показывают комплексные числа передаточной функции в зависимости от частоты.
В случае линейных динамических систем передаточная функция G является по существу оператором, который берет вход u линейной системы к выходу y:
Для системы непрерывного времени передаточная функция связывает Преобразования Лапласа входа U (s) и выход Y (s):
В этом случае функция частоты G (iω) является передаточной функцией, оцененной на мнимой оси s =iω.
Для системы дискретного времени, произведенной с временным интервалом T, передаточная функция связывает Z-преобразования входа U (z) и выход Y (z):
В этом случае, функция частоты передаточная функция G (z), оцененный на модульном круге. Аргумент функции частоты масштабируется шагом расчета T, чтобы сделать функцию частоты периодической с частотой дискретизации .
Частотная характеристика линейной динамической модели описывает, как модель реагирует на синусоидальные входные параметры. Если вход u (t) является синусоидой определенной частоты, то выход y (t) является также синусоидой той же частоты. Однако величина ответа отличается от величины входного сигнала, и фаза ответа смещена относительно входного сигнала.
Графики частотных характеристик обеспечивают понимание динамики линейных систем, такой как зависимые частотой усиления, резонансы и сдвиги фазы. Графики частотных характеристик также содержат информацию о требованиях контроллера и достижимых полосах пропускания.
Можно использовать графики частотных характеристик, может помочь подтвердить, как хорошо линейная параметрическая модель, такая как линейный режим ARX, модель в пространстве состояний, или модель частотной характеристики, получает динамику. Например, можно оценить частотную характеристику из данных об оценке с помощью спектрального анализа (непараметрическая модель) и затем построить результат спектрального анализа сверху частотной характеристики параметрических моделей. Поскольку непараметрические и параметрические модели выведены с помощью различных алгоритмов, соглашения между этими увеличениями моделей доверие к параметрическим результатам модели. Для примера использования спектрального анализа, чтобы сравнить модели, смотрите, Идентифицируют Модели Временных рядов в Командной строке.
System Identification Toolbox предоставляет три частотных характеристики, строящие возможности.
Линейные модели ввода - вывода и модели данных частотной характеристики
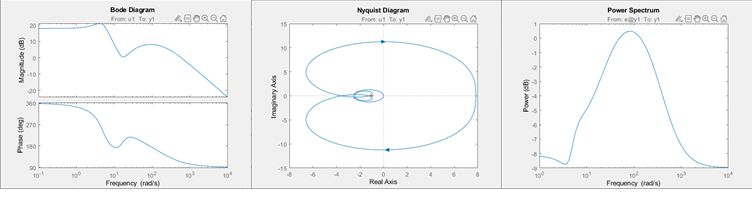
bode— Постройте величину и фазу частотной характеристики по логарифмической шкале частоты. Диаграмма Боде состоит из двух графиков. Главный график показывает величину которым передаточная функция G увеличивает амплитуду синусоидального входа. Нижний график показывает фазу которым передаточная функция переключает вход. Вход к системе является синусоидой, и выход является также синусоидой с той же частотой.
В приложении System Identification используйте опцию Frequency resp в Model Views, чтобы создать Диаграмму Боде.
nyquist— Постройте мнимое по сравнению с действительными частями передаточной функции. Если ваша модель находится в форме кроме передаточной функции, nyquist сначала преобразует модель в передаточную функцию. Можно получить годографы Найквиста только в командной строке.
Все линейные модели, включая временные ряды (никакой вход) модели:
spectrum— Постройте спектр выходной мощности модели временных рядов или спектр воздействия линейной модели ввода - вывода. Спектр воздействия также называется шумовым спектром. Этот график совпадает с Диаграммой Боде ответа модели, но это показывает спектр выходной мощности шумовой модели вместо этого. Для получения дополнительной информации см. Шумовые Графики Спектра.
В приложении System Identification используйте опцию Noise spectrum в Model Views, чтобы создать график спектра мощности.
Рисунок показывает три типа частотного графика, все сгенерированные в командной строке.
Если вы хотите настроить внешний вид графика или включить область доверия программно, использовать bodeplot, nyquistplot, или spectrumplot.
Для примеров и подробной информации о каждой команде, смотрите соответствующие страницы с описанием. Для получения информации о получении частотной характеристики в приложении System Identification смотрите, Идентифицируют Линейные Модели Используя Приложение System Identification, Диаграммы Боде Графика Используя Приложение System Identification и График Шумовой Спектр Используя Приложение System Identification.
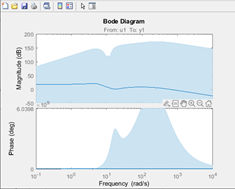
В дополнение к кривой частотной характеристики можно отобразить область, которая представляет доверительный интервал на графике.
Чтобы отобразить доверительный интервал для графика, сгенерированного в командной строке, щелкните правой кнопкой по графику и выберите Characteristics > Confidence region. По умолчанию график отображает область для одного стандартного отклонения, или 95%. Чтобы изменить интервал, щелкните правой кнопкой по графику и выберите Properties. Затем во вкладке Options Property Editor измените Number of standard deviations to display.
Чтобы отобразить доверительный интервал в приложении, выберите Options > Show 97% confidence intervals, или для различного интервала размера, выберите из Options > Set Confidence level.
Доверительный интервал соответствует области значений значений отклика с определенной вероятностью того, чтобы быть фактическим ответом системы. Тулбокс использует оцененную неопределенность в параметрах модели, чтобы вычислить доверительные интервалы и принимает, что оценки имеют Распределение Гаусса.
Например, для 95%-го доверительного интервала, область вокруг номинальной кривой представляет область значений, где существует 95%-й шанс, что это содержит истинный отклик системы. Можно задать доверительный интервал как вероятность (между 0 и 1) или как количество стандартных отклонений Распределения Гаусса. Например, вероятность 0,99 (99%) соответствует 2,58 стандартным отклонениям.
Рисунок показывает пример области доверия для диаграммы Боде, сгенерированной в командной строке.
spectrumplot | spectrum | nyquistplot | nyquist | bodeplot | bode