Годограф Найквиста частотной характеристики
nyquist( создает годограф Найквиста частотной характеристики модели
sys)sys динамической системы. График отображает действительные и мнимые части отклика системы в зависимости от частоты.
nyquist строит контур, состоявший и из положительных и из отрицательных частот. График также показывает стрелы, чтобы указать на направление увеличивающейся частоты для каждой ветви. nyquist автоматически определяет частоты, чтобы построить на основе системной динамики.
Если sys мультивход, мультивыходная модель (MIMO), затем nyquist производит массив годографов Найквиста, каждый график, показывающий частотную характеристику одной пары ввода-вывода.
Если sys модель с комплексными коэффициентами, затем положительные и отрицательные ветви не симметричны.
nyquist(___, отклики системы графиков для частот заданы w)w.
Если w массив ячеек формы {wmin,wmax}то nyquist строит ответ на частотах, располагающихся между wmin и wmax.
Если w вектор из частот, затем nyquist строит ответ на каждой заданной частоте. Векторный w может содержать и отрицательные и положительные частоты.
Можно использовать w с любой из комбинаций входных аргументов в предыдущих синтаксисах.
Когда вам будут нужны дополнительные опции настройки графика, использовать nyquistplot вместо этого.
Две опции изменения масштаба, которые применяются в частности к годографам Найквиста, доступны из контекстного меню:
Full View — Отсекает неограниченные ветви годографа Найквиста, но все еще включает критическую точку (–1, 0).
Zoom on (-1,0) — Изменения масштаба вокруг критической точки (–1, 0). К изменению масштаба критической точки доступа программно, используйте zoomcp команда. Для получения дополнительной информации смотрите nyquistplot.
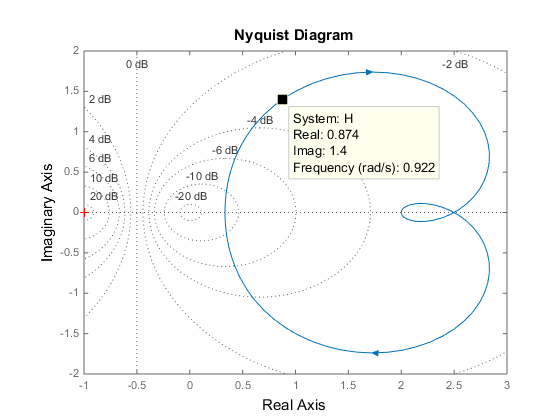
Чтобы активировать маркеры данных, которые отображают действительные и мнимые значения на данной частоте, щелкните где угодно на кривой. Следующий рисунок показывает a nyquist постройте с маркером данных.
sigma (Control System Toolbox) | bode | nyquistplot