Задача оптимизации

Обзор

Прогнозирующее управление модели решает задачу оптимизации – а именно, квадратичная программа (QP) – в каждом контрольном интервале. Решение определяет переменные, которыми управляют (MVS), который будет использоваться на объекте до следующего контрольного интервала.

Эта проблема QP включает следующие функции:

Цель, или "стоимость", функция — скаляр, неотрицательная мера эффективности контроллера, которая будет минимизирована.
Ограничения — Обусловливают решение, должен удовлетворить, такие как физические границы на выходных переменных объекта и MVS.
Решение — корректировки мВ, которые минимизируют функцию стоимости при удовлетворении ограничениям.

Следующие разделы описывают эти функции более подробно.

Стандартная функция стоимости

Стандартная функция стоимости является суммой четырех терминов, каждый фокусирующийся на конкретном аспекте эффективности контроллера, можно следующим образом:

$J (z_{k}) = J_{y} (z_{k}) + J_{u} (z_{k}) + J_{Δ u} (z_{k}) + J_{ε} (z_{k}) .$

Здесь, _zk является решением QP. Аналогичный описанному ниже, каждый термин включает веса, которые помогают вам сбалансировать конкурирующие цели. В то время как контроллер MPC обеспечивает веса по умолчанию, необходимо будет обычно настраивать их, чтобы настроить контроллер для приложения.

Выведите отслеживание уставки

В большинстве приложений контроллер должен сохранить выбранный объект выходными параметрами в или около заданных ссылочных значений. Диспетчер MPC использует следующий скалярный критерий качества работы для выходного отслеживания уставки:

$J_{y} (z_{k}) = \sum_{j = 1}^{n_{y}} \sum_{i = 1}^{p} {\frac{w_{i, j}^{y}}{s_{j}^{y}} [r_{j} (k + i | k) - y_{j} (k + i | k)]}^{2} .$

Здесь,

k Текущий контрольный интервал.
p Горизонт предсказания (количество интервалов).
_ny — Количество выходных переменных объекта.
_zk — Решение QP, данное:
$z_{k}^{T} = [\begin{matrix} u {(k | k)}^{T} & u {(k + 1 | k)}^{T} & \dots & u {(k + p - 1 | k)}^{T} & ε_{k} \end{matrix}] .$
_yj (k +i|k) — Ожидаемое значение j th объект выход в i th шаг горизонта предсказания, в технических модулях.
_rj (k +i|k) — Ссылочное значение для j th объект выход в i th шаг горизонта предсказания, в технических модулях.
$s_{j}^{y}$ — Масштабный коэффициент для j th объект выход, в технических модулях.
$w_{i, j}^{y}$ — Настройка веса для j th объект выход в i th (безразмерный) шаг горизонта предсказания.

Значения _ny, p, $s_{j}^{y}$ , и $w_{i, j}^{y}$ постоянные технические требования контроллера. Контроллер получает ссылочные значения, _rj (k +i|k), для целого горизонта предсказания. Диспетчер использует наблюдателя состояния, чтобы предсказать объект выходные параметры, _yj (k +i|k), которые зависят от переменных корректировок, которыми управляют (_zk), измеренные воздействия (MD), и утверждают оценки. В интервале k, оценки состояния контроллера и значения MD доступны. Поэтому _Jy является функцией _zk только.

Переменное отслеживание, которым управляют,

В некоторых приложениях, такой как тогда, когда существуют переменные, которыми более управляют, чем объект выходные параметры, контроллер должен сохранить выбранные переменные, которыми управляют (MVS) в или около заданных целевых значений. Диспетчер MPC использует следующий скалярный критерий качества работы для переменного отслеживания, которым управляют:

$J_{u} (z_{k}) = \sum_{j = 1}^{n_{u}} \sum_{i = 0}^{p - 1} {\frac{w_{i, j}^{u}}{s_{j}^{u}} [u_{j} (k + i | k) - u_{j, t a r g e t} (k + i | k)]}^{2} .$

Здесь,

k Текущий контрольный интервал.
p Горизонт предсказания (количество интервалов).
_\nu Количество переменных, которыми управляют.
_zk — Решение QP, данное:
$z_{k}^{T} = [\begin{matrix} u {(k | k)}^{T} & u {(k + 1 | k)}^{T} & \dots & u {(k + p - 1 | k)}^{T} & ε_{k} \end{matrix}] .$
_uj,target (k +i|k) — Целевое значение для j th мВ в i th шаг горизонта предсказания, в технических модулях.
$s_{j}^{u}$ — Масштабный коэффициент для j th мВ, в технических модулях.
$w_{i, j}^{u}$ — Настройка веса для j th мВ в i th (безразмерный) шаг горизонта предсказания.

Значения _nu, p, $s_{j}^{u}$ , и $w_{i, j}^{u}$ постоянные технические требования контроллера. Контроллер получает _uj,target (k +i|k) значения для целого горизонта. Диспетчер использует наблюдателя состояния, чтобы предсказать объект выходные параметры. Таким образом _Ju является функцией _zk только.

Подавление переменной Move, которым управляют,

Большинство приложений предпочитает маленькие корректировки мВ (moves). MPC постоянные употребления следующий скалярный критерий качества работы для подавления переменной move, которым управляют:

$J_{Δ u} (z_{k}) = \sum_{j = 1}^{n_{u}} \sum_{i = 0}^{p - 1} {\frac{w_{i, j}^{Δ u}}{s_{j}^{u}} [u_{j} (k + i | k) - u_{j} (k + i - 1 | k)]}^{2} .$

Здесь,

k Текущий контрольный интервал.
p Горизонт предсказания (количество интервалов).
_\nu Количество переменных, которыми управляют.
_zk — Решение QP, данное:
$z_{k}^{T} = [\begin{matrix} u {(k | k)}^{T} & u {(k + 1 | k)}^{T} & \dots & u {(k + p - 1 | k)}^{T} & ε_{k} \end{matrix}] .$
$s_{j}^{u}$ — Масштабный коэффициент для j th мВ, в технических модулях.
$w_{i, j}^{Δ u}$ — Настройка веса для j th перемещение мВ в i th (безразмерный) шаг горизонта предсказания.

Значения _nu, p, $s_{j}^{u}$ , и $w_{i, j}^{Δ u}$ постоянные технические требования контроллера. u (k –1|k) = u (k –1), которые являются известным MVS от предыдущего контрольного интервала. _JΔu является функцией _zk только.

Кроме того, горизонт управления m <p (или блокирование мВ) ограничивает определенные перемещения мВ быть нулем.

Нарушение ограничений

На практике нарушения ограничений могут быть неизбежными. Мягкие ограничения позволяют выполнимое решение QP в таких условиях. Контроллер MPC использует безразмерную, неотрицательную слабую переменную, _εk, который определяет количество нарушения ограничений худшего случая. (См. Ограничения), соответствующий критерий качества работы:

$J_{ε} (z_{k}) = ρ_{ε} ε_{k}^{2} .$

Здесь,

_zk — Решение QP, данное:
$z_{k}^{T} = [\begin{matrix} u {(k | k)}^{T} & u {(k + 1 | k)}^{T} & \dots & u {(k + p - 1 | k)}^{T} & ε_{k} \end{matrix}] .$
Переменная _εk — Slack в контрольном интервале (безразмерный) k.
_ρε — (Безразмерный) вес штрафа нарушения ограничений.

Альтернативная функция стоимости

Можно выбрать использовать следующую альтернативу стандартной функции стоимости:

$J (z_{k}) = \sum_{i = 0}^{p - 1} {[e_{y}^{T} (k + i) Q e_{y} (k + i)] + [e_{u}^{T} (k + i) R_{u} e_{u} (k + i)] + [Δ u^{T} (k + i) R_{Δ u} Δ u (k + i)]} + ρ_{ϵ} ε_{k}^{2} .$

Здесь, Q (_ny-by-_ny), _Ru и _RΔu (_nu-by-_nu) является положительными полу определенными матрицами веса, и:

$\begin{matrix} e_{y} (i + k) = S_{y}^{- 1} [r (k + i + 1 | k) - y (k + i + 1 | k)] \\ e_{u} (i + k) = S_{u}^{- 1} [u_{t a r g e t} (k + i | k) - u (k + i | k)] \\ Δ u (k + i) = S_{u}^{- 1} [u (k + i | k) - u (k + i - 1 | k)] . \end{matrix}$

Кроме того,

_Sy — Диагональная матрица масштабных коэффициентов выходной переменной объекта, в технических модулях.
_Su — Диагональная матрица масштабных коэффициентов мВ в технических модулях.
r (k +1|k) — объект _ny выходные значения ссылки в i th шаг горизонта предсказания, в технических модулях.
y (k +1|k) — объект _ny выходные параметры в i th шаг горизонта предсказания, в технических модулях.
_zk — Решение QP, данное:
$z_{k}^{T} = [\begin{matrix} u {(k | k)}^{T} & u {(k + 1 | k)}^{T} & \dots & u {(k + p - 1 | k)}^{T} & ε_{k} \end{matrix}] .$
_utarget (k +i|k) — целевые значения мВ _nu, соответствующие u (k +i|k), в технических модулях.

Выведите использование предсказаний наблюдатель состояния, как в стандартной функции стоимости.

Альтернативная функция стоимости позволяет недиагональное взвешивание, но требует, чтобы веса были идентичны на каждом шаге горизонта предсказания.

Альтернативные и стандартные функции стоимости идентичны, если следующие условия содержат:

Стандартные функции стоимости используют веса $w_{i, j}^{y}$ , $w_{i, j}^{u}$ , и $w_{i, j}^{Δ u}$ это постоянно относительно индекса, i = 1:p.
Матрицы Q, _Ru и _RΔu являются диагональными с квадратами тех весов как диагональные элементы.

Ограничения

Определенные ограничения неявны. Например, горизонт управления m <p (или блокирование мВ) обеспечивает некоторый шаг мВ, чтобы быть нулем и наблюдателем состояния, используемым для объекта, выходное предсказание является набором неявных ограничений равенства. Явные ограничения, которые можно сконфигурировать, описаны ниже.

Границы на объекте Выходные параметры, MVS и шаг мВ

Наиболее распространенные ограничения MPC являются границами, можно следующим образом.

$\begin{matrix} \frac{y_{j, m i n} (i)}{s_{j}^{y}} - ε_{k} V_{j, m i n}^{y} (i) \leq \frac{y_{j} (k + i | k)}{s_{j}^{y}} \leq \frac{y_{j, m a x} (i)}{s_{j}^{y}} + ε_{k} V_{j, m a x}^{y} (i), i = 1 : p, j = 1 : n_{y} \\ \frac{u_{j, m i n} (i)}{s_{j}^{u}} - ε_{k} V_{j, m i n}^{u} (i) \leq \frac{u_{j} (k + i - 1 | k)}{s_{j}^{u}} \leq \frac{u_{j, m a x} (i)}{s_{j}^{u}} + ε_{k} V_{j, m a x}^{u} (i), i = 1 : p, j = 1 : n_{u} \\ \frac{Δ u_{j, m i n} (i)}{s_{j}^{u}} - ε_{k} V_{j, m i n}^{Δ u} (i) \leq \frac{Δ u_{j} (k + i - 1 | k)}{s_{j}^{u}} \leq \frac{Δ u_{j, m a x} (i)}{s_{j}^{u}} + ε_{k} V_{j, m a x}^{Δ u} (i), i = 1 : p, j = 1 : n_{u} . \end{matrix}$

Здесь, параметры V (значения ECR) являются безразмерными константами контроллера, аналогичными весам функции стоимости, но используемыми для ограничительного смягчения (см., что Ограничение Смягчается). Кроме того,

_εk — Скалярные QP ослабляют переменную (безразмерную) используемый для ограничительного смягчения.
$s_{j}^{y}$ — Масштабный коэффициент для j th объект выход, в технических модулях.
$s_{j}^{u}$ — Масштабный коэффициент для j th мВ, в технических модулях.
y _{j, min} (i), y _{j, макс.} (i) — нижние и верхние границы для j th объект выход в i th шаг горизонта предсказания, в технических модулях.
u _{j, min} (i), u _{j, макс.} (i) — нижние и верхние границы для j th мВ в i th шаг горизонта предсказания, в технических модулях.
Δu _{j, min} (i), Δu _{j, макс.} (i) — нижние и верхние границы для j th мВ, постепенно увеличивает в i th шаг горизонта предсказания в технических модулях.

За исключением слабого переменного условия неотрицательности, все вышеупомянутые ограничения являются дополнительными и являются неактивными по умолчанию (i.e., инициализированный бесконечными предельными значениями). Чтобы включать связанное ограничение, необходимо задать конечный предел, когда вы проектируете контроллер.

Матрицы QP

В этом разделе описываются матрицы, сопоставленные с прогнозирующей задачей оптимизации управления модели, описанной в Задаче оптимизации.

Предсказание

Примите, что возмущения, описанные во Входном Возмущении, являются модульными усилениями; то есть, d (k) = _nd (k) является белым Гауссовым шумом. Можно обозначить эту проблему как

$x \leftarrow [\begin{matrix} x \\ x_{d} \end{matrix}], A \leftarrow [\begin{matrix} A & B_{d} \bar{C} \\ 0 & \bar{A} \end{matrix}], B_{u} \leftarrow [\begin{matrix} B_{u} \\ 0 \end{matrix}], B_{v} \leftarrow [\begin{matrix} B v \\ 0 \end{matrix}], B_{d} \leftarrow [\begin{matrix} B_{d} \bar{D} \\ \bar{B} \end{matrix}], C \leftarrow [\begin{matrix} C & D_{d} \bar{C} \end{matrix}]$

Затем модель предсказания:

x (k +1) = A x (k) _+Buu (k) _+Bvv (k) _+Bd_nd (k)

y (k) = C x (k) _+Dvv (k) _+Dd_nd (k)

Затем рассмотрите задачу предсказания будущих траекторий модели, выполняемой во время k=0. Установите _{без обозначения даты} (i) =0 в течение всех моментов предсказания i и получите

$y (i | 0) = C [A^{i} x (0) + \sum_{h = 0}^{i - 1} A^{i - 1} (B_{u} (u (- 1) + \sum_{j = 0}^{h} Δ u (j)) + B_{v} v (h))] + D_{v} v (i)$

Это уравнение дает решение

$[\begin{matrix} y (1) \\ \dots \\ y (p) \end{matrix}] = S_{x} x (0) + S_{u 1} u (- 1) + S_{u} [\begin{matrix} Δ u (0) \\ \dots \\ Δ u (p - 1) \end{matrix}] + H_{v} [\begin{matrix} v (0) \\ \dots \\ v (p) \end{matrix}]$

где

$\begin{array}{l} S_{x} = [\begin{matrix} C A \\ C A^{2} \\ \dots \\ C A^{p} \end{matrix}] \in ℜ^{p n_{y} \times n_{x}}, S_{u 1} = [\begin{matrix} C B_{u} \\ C B_{u} + C A B_{u} \\ \dots \\ \sum_{h = 0}^{p - 1} C A^{h} B_{u} \end{matrix}] \in ℜ^{p n_{y} \times n_{u}} \\ S_{u} = [\begin{matrix} C B_{u} & 0 & \dots & 0 \\ C B_{u} + C A B_{u} & C B_{u} & \dots & 0 \\ \dots & \dots & \dots & \dots \\ \sum_{h = 0}^{p - 1} C A^{h} B_{u} & \sum_{h = 0}^{p - 2} C A^{h} B_{u} & \dots & C B_{u} \end{matrix}] \in ℜ^{p n_{y} \times p n_{u}} \\ H_{v} = [\begin{matrix} C B_{v} & D_{v} & 0 & \dots & 0 \\ C A B_{v} & C B_{v} & D_{v} & \dots & 0 \\ \dots & \dots & \dots & \dots & \dots \\ C A^{p - 1} B_{v} & C A^{p - 2} B_{v} & C A^{p - 3} B_{v} & \dots & D_{v} \end{matrix}] \in ℜ^{p n_{y} \times (p + 1) n_{v}} . \end{array}$

Переменные оптимизации

Позвольте m быть количеством свободных перемещений управления и позволить z = [z0;...; zm–1]. То,

$[\begin{matrix} Δ u (0) \\ \dots \\ Δ u (p - 1) \end{matrix}] = J_{M} [\begin{matrix} z_{0} \\ \dots \\ z_{m - 1} \end{matrix}]$

где J _M зависит от выбора блокирования перемещений. Вместе со слабой переменной ɛ, векторы z ₀..., z _{m –1} составляет свободные переменные оптимизации задачи оптимизации. В случае систем с одной переменной, которой управляют, z ₀..., z _{m –1} является скалярами.

Считайте блокирующиеся перемещения изображенными в следующем графике.

Блокирование Перемещений: Входные параметры и Входной Шаг для перемещений = [2 3 2]

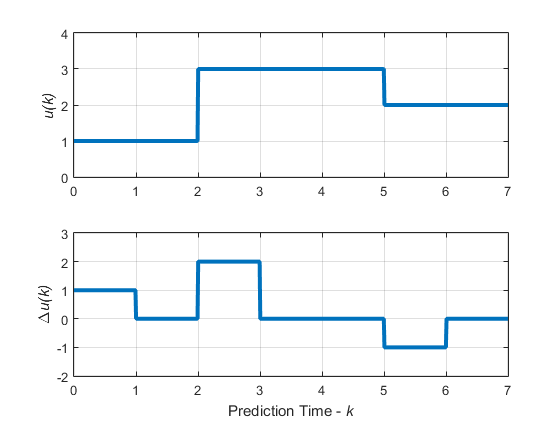
Этот график соответствует выбору moves=[2 3 2], или эквивалентно, u (0) =u (1), u (2) =u (3) =u (4), u (5) =u (6), Δ u (0) =z0, Δ u (2) =z1, Δ u (5) =z2, Δ u (1) = Δ u (3) = Δ u (4) = Δ u (6) =0.

Затем соответствующий матричный _JM

$J_{M} = [\begin{matrix} I & 0 & 0 \\ 0 & 0 & 0 \\ 0 & I & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & I \\ 0 & 0 & 0 \end{matrix}]$

Для получения дополнительной информации о переменном блокировании, которым управляют смотрите Переменное Блокирование, которым Управляют.

Функция стоимости

Стандартная Форма. Функция, которая будет оптимизирована,

$\begin{array}{l} J (z, ε) = {([\begin{matrix} u (0) \\ \dots \\ u (p - 1) \end{matrix}] - [\begin{matrix} u_{t a r g e t} (0) \\ \dots \\ u_{t a r g e t} (p - 1) \end{matrix}])}^{T} W_{u}^{2} ([\begin{matrix} u (0) \\ \dots \\ u (p - 1) \end{matrix}] - [\begin{matrix} u_{t a r g e t} (0) \\ \dots \\ u_{t a r g e t} (p - 1) \end{matrix}]) + {[\begin{matrix} Δ u (0) \\ \dots \\ Δ u (p - 1) \end{matrix}]}^{T} W_{Δ u}^{2} [\begin{matrix} Δ u (0) \\ \dots \\ Δ u (p - 1) \end{matrix}] \\ + {([\begin{matrix} y (1) \\ \dots \\ y (p) \end{matrix}] - [\begin{matrix} r (1) \\ \dots \\ r (p) \end{matrix}])}^{T} W_{y}^{2} ([\begin{matrix} y (1) \\ \dots \\ y (p) \end{matrix}] - [\begin{matrix} r (1) \\ \dots \\ r (p) \end{matrix}]) + ρ_{ε} ε^{2} \end{array}$

где

\begin{matrix} W_{u} = diag (w_{0, 1}^{u}, w_{0, 2}^{u}, ..., w_{0, n_{u}}^{u}, ..., w_{p - 1, 1}^{u}, w_{p - 1, 2}^{u}, ..., w_{p - 1, n_{u}}^{u}) \\ W_{Δ u} = diag (w_{0, 1}^{Δ u}, w_{0, 2}^{Δ u}, ..., w_{0, n_{u}}^{Δ u}, ..., w_{p - 1, 1}^{Δ u}, w_{p - 1, 2}^{Δ u}, ..., w_{p - 1, n_{u}}^{Δ u}) \\ W_{y} = diag (w_{1, 1}^{y}, w_{1, 2}^{y}, ..., w_{1, n_{y}}^{y}, ..., w_{p, 1}^{y}, w_{p, 2}^{y}, ..., w_{p, n_{y}}^{y}) \end{matrix}

(1)

Наконец, после замены u (k), Δu (k), y (k), J (z) может быть переписан как

\begin{array}{l} J (z, ε) = ρ_{ε} ε^{2} + z^{T} K_{Δ u} z + 2 ({[\begin{matrix} r (1) \\ \dots \\ r (p) \end{matrix}]}^{T} K_{r} + {[\begin{matrix} v (0) \\ \dots \\ v (p) \end{matrix}]}^{T} K_{v} + u {(- 1)}^{T} K_{u} + {[\begin{matrix} u_{t a r g e t} (0) \\ \dots \\ u_{t a r g e t} (p - 1) \end{matrix}]}^{T} K_{u t} + x {(0)}^{T} K_{x}) z \\ + c_{y}^{T} W_{y} c_{y} + c_{u}^{T} W_{u} c_{u} \end{array}

(2)

где

$\begin{array}{l} c_{y} = S_{x} x (0) + S_{u 1} u (- 1) + H_{v} [\begin{matrix} v (0) \\ \dots \\ v (p) \end{matrix}] - [\begin{matrix} r (1) \\ \dots \\ r (p) \end{matrix}] \\ c_{u} = [\begin{matrix} I_{1} \\ \dots \\ I_{p} \end{matrix}] u (- 1) - [\begin{matrix} u_{t a r g e t} (0) \\ \dots \\ u_{t a r g e t} (p - 1) \end{matrix}] \end{array}$

Здесь, I ₁ = … = I _p является единичными матрицами размера _nu.

Примечание

Можно хотеть проблему QP остаться строго выпуклыми. Если число обусловленности матрицы Гессиана _KΔU больше, чем 10¹², добавьте количество 10*sqrt(eps) на каждом диагональном термине. Можно использовать это решение только, когда все входные уровни не оштрафованы (W^Δ^u=0) (см. Weights свойство mpc объект.

Альтернативная Функция стоимости. Если вы используете альтернативную функцию стоимости, показанную в Альтернативной Функции стоимости, то уравнение 1 заменяется следующим:

\begin{array}{l} W_{u} = blkdiag (R_{u}, ..., R_{u}) \\ W_{Δ u} = blkdiag (R_{Δ u}, ..., R_{Δ u}) \\ W_{y} = blkdiag (Q, ..., Q) \end{array}

(3)

В этом случае диагональные блоком матрицы повторяют p времена, например, однажды для каждого шага в горизонте предсказания.

У вас также есть опция, чтобы использовать комбинацию стандартных и альтернативных форм. Для получения дополнительной информации смотрите Weights свойство mpc объект.

Ограничения

Затем рассмотрите пределы на входных параметрах, введите шаг и выходные параметры наряду с ограничением ɛ≥ 0.

$[\begin{matrix} y_{\min} (1) - ε V_{\min}^{y} (1) \\ \dots \\ y_{\min} (p) - ε V_{\min}^{y} (p) \\ u_{\min} (0) - ε V_{\min}^{u} (0) \\ \dots \\ u_{\min} (p - 1) - ε V_{\min}^{u} (p - 1) \\ Δ u_{\min} (0) - ε V_{\min}^{Δ u} (0) \\ \dots \\ Δ u_{\min} (p - 1) - ε V_{\min}^{Δ u} (p - 1) \end{matrix}] \leq [\begin{matrix} y (1) \\ \dots \\ y (p) \\ u (0) \\ \dots \\ u (p - 1) \\ Δ u (0) \\ \dots \\ Δ u (p - 1) \end{matrix}] \leq [\begin{matrix} y_{\max} (1) + ε V_{\max}^{y} (1) \\ \dots \\ y_{\max} (p) + ε V_{\max}^{y} (p) \\ u_{\max} (0) + ε V_{\max}^{u} (0) \\ \dots \\ u_{\max} (p - 1) + ε V_{\max}^{u} (p - 1) \\ Δ u_{\max} (0) + ε V_{\max}^{Δ u} (0) \\ \dots \\ Δ u_{\max} (p - 1) + ε V_{\max}^{Δ u} (p - 1) \end{matrix}]$

Примечание

Чтобы уменьшать вычислительное усилие, контроллер автоматически устраняет посторонние ограничения, такие как бесконечные границы. Таким образом ограничительное множество, используемое в режиме реального времени, может быть намного меньшим, чем предложенный в этом разделе.

Подобно тому, что вы сделали для функции стоимости, можно заменить u (k), Δu (k), y (k), и получить

M_{z} z + M_{ε} ε \leq M_{\lim} + M_{v} [\begin{matrix} v (0) \\ \dots \\ v (p) \end{matrix}] + M_{u} u (- 1) + M_{x} x (0)

(4)

В этом случае матрицы _Mz, M _ɛ, Mlim, _Mv, _Му и _Mx получены из верхних и нижних границ и значений ECR.

Неограниченное прогнозирующее управление модели

Оптимальное решение вычисляется аналитически

$z * = - K_{Δ u}^{- 1} {({[\begin{matrix} r (1) \\ \dots \\ r (p) \end{matrix}]}^{T} K_{r} + [\begin{matrix} v (0) \\ \dots \\ v (p) \end{matrix}] K_{v} + u {(- 1)}^{T} K_{u} + {[\begin{matrix} u_{t a r g e t} (0) \\ \dots \\ u_{t a r g e t} (p - 1) \end{matrix}]}^{T} K_{u t} + x {(0)}^{T} K_{x})}^{T}$

и прогнозирующий контроллер модели устанавливает Δu (k) =z*0, u (k) =u (k–1) + Δu (k).

Документация