Exponenta Banner

Inverse Kinematics

Вычислите объединенные настройки, чтобы достигнуть положения исполнительного элемента конца

расширьте все на странице
  • Библиотека:

  • Robotics System Toolbox / Алгоритмы Манипулятора

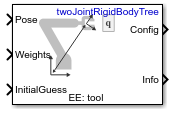
  • Inverse Kinematics block

Описание

Блок Inverse Kinematics использует решатель кинематической инверсии (IK), чтобы вычислить объединенные настройки для желаемого положения исполнительного элемента конца на основе заданной модели дерева твердого тела. Создайте модель дерева твердого тела для своего робота с помощью rigidBodyTree класс. Модель дерева твердого тела задает все объединенные ограничения, которые осуществляет решатель.

Задайте RigidBodyTree параметр и желаемый исполнительный элемент конца в маске блока. Можно также настроить параметры алгоритма во вкладке Solver Parameters.

Введите желаемый исполнительный элемент конца Pose, Weights на допуске положения и InitialGuess для объединенной настройки. Решатель выводит настройку робота, Config, который удовлетворяет положению исполнительного элемента конца в допусках, заданных во вкладке Solver Parameters.

Порты

Входной параметр

развернуть все

Положение исполнительного элемента конца в виде гомогенного преобразования 4 на 4. Это преобразование задает желаемое положение и ориентацию твердого тела, заданного в параметре End effector.

Типы данных: single | double

Веса для допусков положения в виде вектора с шестью элементами. Первые три элемента вектора соответствуют весам при ошибке в ориентации для желаемого положения. Последние три элемента вектора соответствуют весам при ошибке в положении xyz для желаемого положения.

Типы данных: single | double

Исходное предположение настройки робота в виде вектора из объединенных положений. Количество положений равно количеству нефиксированных соединений в параметре Rigid body tree. Используйте это исходное предположение, чтобы помочь вести решатель к желаемой настройке робота. Однако решение, как гарантируют, не будет близко к этому исходному предположению.

Типы данных: single | double

Вывод

развернуть все

Настройка робота, которая решает желаемое положение исполнительного элемента конца в виде вектора. Настройка робота является вектором из объединенных положений для модели дерева твердого тела. Количество положений равно количеству нефиксированных соединений в параметре Rigid body tree.

Типы данных: single | double

Информация о решении, возвращенная как шина. Шина информации о решении содержит эти элементы:

  • Iterations — Количество итераций запущено алгоритмом.

  • PoseErrorNorm — Величина ошибки между положением исполнительного элемента конца в решении и желаемым положением исполнительного элемента конца.

  • ExitFlag — Код, который предоставляет больше подробную информацию на осуществлении алгоритма и что заставило его возвращаться. Для выходных флагов каждого типа алгоритма смотрите Выходные Флаги.

  • Status — Вектор символов, описывающий, является ли решение в допуске (1) или самое лучшее решение, которое мог найти алгоритм (2).

Параметры

развернуть все

Параметры блоков

Модель дерева твердого тела в виде rigidBodyTree объект. Создайте модель робота в MATLAB® рабочая область прежде, чем задать в маске блока.

Имя исполнительного элемента конца для желаемого положения. Видеть список тел на rigidBodyTree возразите, задайте параметр Rigid body tree, затем нажмите Select body.

Выберите, чтобы включить порт Info и получить диагностическую информацию для решения для решателя.

Параметры решателя

Алгоритм для решения инверсной кинематики в виде любого 'BFGSGradientProjection' или 'LevenbergMarquardt'. Для получения дополнительной информации каждого алгоритма, см. Алгоритмы Инверсной кинематики.

Выберите, чтобы осуществить объединенные пределы, заданные в модели Rigid body tree.

Максимальное количество итераций, чтобы оптимизировать решение в виде положительного целого числа. Увеличение числа итераций может улучшить решение за счет времени выполнения.

Максимальное количество секунд, которые алгоритм запускает прежде, чем испытать таймаут в виде положительной скалярной величины. Увеличение максимального времени может улучшить решение за счет времени выполнения.

Порог на градиенте функции стоимости в виде положительной скалярной величины. Алгоритм останавливается, если величина градиента падает ниже этого порога. Низкая величина градиента обычно указывает, что решатель сходился к решению.

Порог на величине ошибки между положением исполнительного элемента конца, сгенерированным из решения и желаемым положением в виде положительной скалярной величины. Weights заданный для каждого компонента положения включены в это вычисление.

Минимальный размер шага позволен решателем в виде положительной скалярной величины. Меньшие размеры шага обычно означают, что решение близко к сходимости.

Порог на изменении в исполнительном элементе конца излагает ошибку между итерациями в виде положительной скалярной величины. Алгоритм возвращается, если изменения во всех элементах ошибки положения меньше, чем этот порог.

Зависимости

Этот параметр включен, когда Solver является Levenberg-Marquadt.

Установите флажок, чтобы включить ошибочное затухание, затем задать Damping bias параметр.

Зависимости

Этот параметр включен, когда Solver является Levenberg-Marquadt.

Затухание на функции стоимости в виде положительной скалярной величины. Алгоритму Levenberg-Marquadt управлял функцией затухания этот скаляр, который работает с функцией стоимости, чтобы управлять уровнем сходимости.

Зависимости

Этот параметр включен, когда Solver является Levenberg-Marquadt и Use error damping является on.

  • Interpreted execution — Симулируйте модель с помощью интерпретатора MATLAB. Эта опция сокращает время запуска, но имеет более медленную скорость симуляции, чем Code generation. В этом режиме можно отладить исходный код блока.

  • Code generation — Симулируйте модель с помощью сгенерированного кода C. В первый раз вы запускаете симуляцию, Simulink® генерирует код С для блока. Код С снова используется для последующих симуляций, пока модель не изменяется. Эта опция требует дополнительного времени запуска, но скорость последующих симуляций сопоставима с Interpreted execution.

Настраиваемый: нет

Примеры модели

Trace An End-Effector Trajectory with Inverse Kinematics in Simulink

Проследите траекторию исполнительного элемента конца с инверсной кинематикой в Simulink

Используйте модель робота твердого тела, чтобы вычислить инверсную кинематику с помощью Simulink®. Задайте траекторию для исполнительного элемента конца робота и цикла через точки, чтобы решить настройки робота, которые прослеживают эту траекторию.

Ссылки

[1] Badreddine, Хасан, Стефан Вэндьюалл и Йохан Мейерс. "Последовательное квадратичное программирование (SQP) для Оптимального управления в Прямой Числовой Симуляции Турбулентного течения". Журнал Вычислительной Физики. 256 (2014): 1–16. doi:10.1016/j.jcp.2013.08.044.

[2] Bertsekas, нелинейное программирование Димитри П. Белмонт, MA: научная Афина, 1999.

[3] Goldfarb, Дональд. "Расширение Переменного Метрического Метода Дэвидона к Максимизации Под Линейным Неравенством и Ограничениями равенства". SIAM Journal на Прикладной математике. Издание 17, № 4 (1969): 739–64. doi:10.1137/0117067.

[4] Nocedal, Хорхе и Стивен Райт. Числовая оптимизация. Нью-Йорк, Нью-Йорк: Спрингер, 2006.

[5] Sugihara, Tomomichi. "Беззаботная к разрешимости Инверсная кинематика Методом Levenberg–Marquardt". Транзакции IEEE на Робототехнике. Издание 27, № 5 (2011): 984–91. doi:10.1109/tro.2011.2148230.

[6] Чжао, Jianmin и Норман Ай. Бэдлер. "Расположение Инверсной кинематики Используя Нелинейное программирование для Высоко Ясно сформулированных фигур". Транзакции ACM на Графике. Издание 13, № 4 (1994): 313–36. doi:10.1145/195826.195827.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Смотрите также

Объекты

Блоки

Темы

Введенный в R2018b

Документация Robotics System Toolbox

Поддержка