Снижение сложности модели из нормированной взаимно-простой факторизации
ncfmr вычисляет приближение уменьшаемого порядка модели путем усечения режимов во взаимно-простой факторизации модели полного порядка. Этот метод связан со сбалансированным методом усечения balred, но это является особенно подходящим к сокращению порядка контроллера. Для стабилизировавшегося контроллера уменьшаемый контроллер также стабилизировался, пока ошибка приближения меньше, чем поле робастности, вычисленное ncfmargin.
[ вычисляет приближение уменьшаемого порядка модели Gred,info] = ncfmr(G,ord)G динамической системы. Задайте желаемый порядок сокращения как ord. Если ord вектор, затем Gred массив приближений соответствующего порядка. Структура info содержит информацию о расчете, таком как границы при ошибке приближения.
[~, вычисляет взаимно-простую факторизацию info] = ncfmr(G)G данный [M,N] таким образом, что G = M\N (см. lncf), сингулярные значения Ганкеля факторизации и ошибочные границы. Можно использовать эту информацию, чтобы определить целевой порядок сокращения программно на основе желаемой точности или устойчивых факторов устойчивости. Затем используйте синтаксис Gred = ncfmr(G,ord,info) вычислить модель уменьшаемого порядка.
Gred = ncfmr(G,ord,info)info. Получите info с помощью предыдущего синтаксиса, [~,info] = ncfmr(G). Обеспечение ранее вычисленного info к ncfmr позволяет вам выполнять снижение сложности модели, не имея необходимость повторно вычислять факторизацию и сингулярные значения Ганкеля. Этот синтаксис поэтому особенно полезен, когда эффективность является беспокойством.
ncfmr(G) строит сингулярные значения Ганкеля и границы при ошибке приближения, соответствующей каждому порядку. Исследуйте график определить уменьшаемый порядок на основе желаемой точности или устойчивых факторов устойчивости. Можно затем использовать Gred = ncfmr(G,ord) вычислить модель уменьшаемого порядка.
Можно использовать ncfmr уменьшать объект G или контроллер K при сохранении устойчивости с обратной связью следующей SISO или обратной связи MIMO.
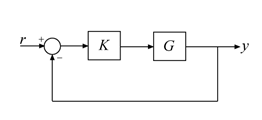
Устойчивость этого цикла сохраняется, пока ошибка приближения уменьшаемого объекта меньше, чем поле робастности для этого цикла, данного ncfmargin(G,K).
Для контроллеров, вычисленных с ncfsyn, сокращение контроллера Ks это ncfsyn вычисляет для имеющего форму контроллера, Gs предпочтителен. И Ks и Gs возвращены ncfsyn в info выходной аргумент. Можно затем вычислить Kr, уменьшаемый контроллер для исходного объекта G, от Kr = W 1KsrW2, где W 1 и W 2 является весами формирования, используемыми с ncfsyn. Для примера смотрите, Уменьшают Порядок Контроллера При Сохранении Устойчивости и Робастности.
Для контроллеров, полученных другими методами, сокращением с ncfmr также устойчивость консервов, если ошибка не превышает ncfmargin поле. Однако такое сокращение может частично удалить интегральное действие и ввести установившиеся ошибки отслеживания. Поэтому удаление любого интегратора называет от диспетчера перед сокращением с ncfmr и заменение их в уменьшаемом контроллере рекомендуется.
ncfmr выполняет следующие шаги, чтобы уменьшать входную модель G до желаемого порядка k.