Найдите локальные максимумы
pks = findpeaks(data)data. Локальный пик является выборкой данных, которая или больше, чем ее две соседних выборки или равна Inf. Non-Inf конечные точки сигнала исключены. Если пик является плоским, функция возвращает только точку с самым низким индексом.
[___] = findpeaks(___, задает аргументы пары "имя-значение" использования опций в дополнение к любому из входных параметров в предыдущих синтаксисах.Name,Value)
findpeaks(___) без выходных аргументов строит сигнал и накладывает пиковые значения.
Задайте вектор с тремя peaks и постройте его.
data = [25 8 15 5 6 10 10 3 1 20 7]; plot(data)

Найдите локальные максимумы. Peaks выводится в порядке вхождения. Первая выборка не включена несмотря на то, чтобы быть максимумом. Для плоского пика функция возвращает только точку с самым низким индексом.
pks = findpeaks(data)
pks = 1×3
15 10 20
Используйте findpeaks без выходных аргументов, чтобы отобразить peaks.
findpeaks(data)

Создайте сигнал, который состоит из суммы кривых нормального распределения. Задайте местоположение, высоту и ширину каждой кривой.
x = linspace(0,1,1000); Pos = [1 2 3 5 7 8]/10; Hgt = [3 4 4 2 2 3]; Wdt = [2 6 3 3 4 6]/100; for n = 1:length(Pos) Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2); end PeakSig = sum(Gauss);
Постройте отдельные кривые и их сумму.
plot(x,Gauss,'--',x,PeakSig)
Используйте findpeaks с настройками по умолчанию, чтобы найти peaks сигнала и их местоположений.
[pks,locs] = findpeaks(PeakSig,x);
Постройте peaks с помощью findpeaks и пометьте их.
findpeaks(PeakSig,x) text(locs+.02,pks,num2str((1:numel(pks))'))

Сортировка peaks от самого высокого до самого короткого.
[psor,lsor] = findpeaks(PeakSig,x,'SortStr','descend'); findpeaks(PeakSig,x) text(lsor+.02,psor,num2str((1:numel(psor))'))

Создайте сигнал, который состоит из суммы кривых нормального распределения, едущих на полном периоде косинуса. Задайте местоположение, высоту и ширину каждой кривой.
x = linspace(0,1,1000); base = 4*cos(2*pi*x); Pos = [1 2 3 5 7 8]/10; Hgt = [3 7 5 5 4 5]; Wdt = [1 3 3 4 2 3]/100; for n = 1:length(Pos) Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2); end PeakSig = sum(Gauss)+base;
Постройте отдельные кривые и их сумму.
plot(x,Gauss,'--',x,PeakSig,x,base)
Используйте findpeaks определять местоположение и строить peaks, который имеет выдающееся положение по крайней мере 4.
findpeaks(PeakSig,x,'MinPeakProminence',4,'Annotate','extents')

Самый высокий и самый низкий peaks является единственными единицами, которые удовлетворяют условию.
Отобразите выдающиеся положения и ширины в половине выдающегося положения всего peaks.
[pks,locs,widths,proms] = findpeaks(PeakSig,x); widths
widths = 1×6
0.0154 0.0431 0.0377 0.0625 0.0274 0.0409
proms
proms = 1×6
2.6816 5.5773 3.1448 4.4171 2.9191 3.6363
Солнечные пятна являются циклическим явлением. Их номер, как известно, достигает максимума примерно каждые 11 лет.
Загрузите файл sunspot.dat, который содержит среднее количество солнечных пятен, наблюдаемых каждый год от 1 700 до 1987. Найдите и постройте максимумы.
load sunspot.dat
year = sunspot(:,1);
avSpots = sunspot(:,2);
findpeaks(avSpots,year)
Улучшите свою оценку длительности цикла путем игнорирования peaks, который является очень друг близко к другу. Найдите и постройте peaks снова, но теперь ограничьте приемлемые разделения от пика к пику значениями, больше, чем шесть лет.
findpeaks(avSpots,year,'MinPeakDistance',6)
Используйте пиковые местоположения, возвращенные findpeaks вычислить средний интервал между максимумами.
[pks,locs] = findpeaks(avSpots,year,'MinPeakDistance',6);
meanCycle = mean(diff(locs))meanCycle = 10.9600
Создайте datetime массив с помощью данных года. Примите, что солнечные пятна считались каждый год 20-го марта, близко к весеннему равноденствию. Найдите пиковые годы солнечного пятна. Используйте years функция, чтобы задать минимальное пиковое разделение как duration.
ty = datetime(year,3,20); [pk,lk] = findpeaks(avSpots,ty,'MinPeakDistance',years(6)); plot(ty,avSpots,lk,pk,'o')

Вычислите средний цикл солнечной активности с помощью datetime функциональность.
dttmCycle = years(mean(diff(lk)))
dttmCycle = 10.9600
Создайте расписание с данными. Задайте переменную времени в годах. Отобразите данные на графике. Покажите последние пять записей расписания.
TT = timetable(years(year),avSpots); plot(TT.Time,TT.Variables)

entries = TT(end-4:end,:)
entries=5×1 timetable
Time avSpots
________ _______
1983 yrs 66.6
1984 yrs 45.9
1985 yrs 17.9
1986 yrs 13.4
1987 yrs 29.3
Загрузите звуковой сигнал, произведенный на уровне 7 418 Гц. Выберите 200 выборок.
load mtlb
select = mtlb(1001:1200);Найдите peaks, который разделяется по крайней мере на 5 мс.
Применять это ограничение, findpeaks выбирает самый высокий пик в сигнале и устраняет весь peaks в 5 мс из него. Функция затем повторяет процедуру для самого высокого остающегося пика и выполняет итерации, пока это не исчерпывает peaks, чтобы рассмотреть.
findpeaks(select,Fs,'MinPeakDistance',0.005)
Найдите peaks, который имеет амплитуду по крайней мере 1 В.
findpeaks(select,Fs,'MinPeakHeight',1)
Найдите peaks, который на по крайней мере 1 В выше, чем их соседние выборки.
findpeaks(select,Fs,'Threshold',1)
Найдите peaks, который понижается по крайней мере на 1 В с обеих сторон, прежде чем сигнал достигает более высокого значения.
findpeaks(select,Fs,'MinPeakProminence',1)
Датчики могут возвратить отсеченные показания, если данные больше, чем данная точка насыщения. Можно принять решение игнорировать этот peaks как бессмысленный или включить их к анализу.
Сгенерируйте сигнал, который состоит из продукта тригонометрических функций частот 5 Гц и 3 Гц, встроенные в белый Гауссов шум отклонения 0,1 ². Сигнал производится в течение одной секунды на уровне 100 Гц. Сбросьте генератор случайных чисел для восстанавливаемых результатов.
rng default
fs = 1e2;
t = 0:1/fs:1-1/fs;
s = sin(2*pi*5*t).*sin(2*pi*3*t)+randn(size(t))/10;Симулируйте влажное измерение путем усечения каждого чтения, которое больше заданного, связанного 0,32. Постройте влажный сигнал.
bnd = 0.32;
s(s>bnd) = bnd;
plot(t,s)
xlabel('Time (s)')
Найдите peaks сигнала. findpeaks отчеты только возрастающее ребро каждого плоского пика.
[pk,lc] = findpeaks(s,t); hold on plot(lc,pk,'x')

Используйте 'Threshold' пара "имя-значение", чтобы исключить плоский peaks. Потребуйте минимального амплитудного различия между пиком и его соседями.
[pkt,lct] = findpeaks(s,t,'Threshold',1e-4); plot(lct,pkt,'o','MarkerSize',12)

Создайте сигнал, который состоит из суммы кривых нормального распределения. Задайте местоположение, высоту и ширину каждой кривой.
x = linspace(0,1,1000); Pos = [1 2 3 5 7 8]/10; Hgt = [4 4 2 2 2 3]; Wdt = [3 8 4 3 4 6]/100; for n = 1:length(Pos) Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2); end PeakSig = sum(Gauss);
Постройте отдельные кривые и их сумму.
plot(x,Gauss,'--',x,PeakSig)
grid
Измерьте ширины peaks с помощью половины выдающегося положения в качестве ссылки.
findpeaks(PeakSig,x,'Annotate','extents')

Измерьте ширины снова, на этот раз с помощью половины высоты в качестве ссылки.
findpeaks(PeakSig,x,'Annotate','extents','WidthReference','halfheight') title('Signal Peak Widths')

data — Входные данныеВходные данные в виде вектора. data должно быть действительным и должен иметь по крайней мере три элемента.
Типы данных: double | single
x — Местоположенияdatetime массивМестоположения в виде вектора или datetime массив. x должен увеличиться монотонно и иметь ту же длину как data. Если x не использован, затем индексы data используются в качестве местоположений.
Типы данных: double | single | datetime
Fs — Частота дискретизацииЧастота дискретизации в виде положительной скалярной величины. Частота дискретизации является количеством отсчетов в единицу времени. Если модуль времени является секундами, частота дискретизации имеет модули герц.
Типы данных: double | single
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
'SortStr','descend','NPeaks',3 находит три самых высоких peaks сигнала.NPeaks — Максимальное количество peaksМаксимальное количество peaks, чтобы возвратиться в виде разделенной запятой пары, состоящей из 'NPeaks' и положительный целочисленный скаляр. findpeaks действует от первого элемента входных данных и завершает работу, когда количество peaks достигает значения 'NPeaks'.
Типы данных: double | single
SortStr — Пиковая сортировка'none' (значение по умолчанию) | 'ascend' | 'descend'Пиковая сортировка в виде разделенной запятой пары, состоящей из 'SortStr' и одно из этих значений:
'none' возвращает peaks в порядке, в котором они происходят во входных данных.
'ascend' возвращает peaks в возрастании или увеличении порядка, от самого маленького до самого большого значения.
'descend' возвращает peaks в порядке убывания, от самого большого до наименьшего значения.
MinPeakHeight — Минимальная пиковая высота-Inf (значение по умолчанию) | действительный скалярМинимальная пиковая высота в виде разделенной запятой пары, состоящей из 'MinPeakHeight' и действительный скаляр. Используйте этот аргумент, чтобы иметь findpeaks возвратите только тот peaks выше, чем 'MinPeakHeight'. Определение минимальной пиковой высоты может уменьшать время вычислений.
Типы данных: double | single
MinPeakProminence — Минимальное пиковое выдающееся положениеМинимальное пиковое выдающееся положение в виде разделенной запятой пары, состоящей из 'MinPeakProminence' и действительный скаляр. Используйте этот аргумент, чтобы иметь findpeaks возвратите только тот peaks, который имеет относительную важность, по крайней мере, 'MinPeakProminence'. Для получения дополнительной информации смотрите Выдающееся положение.
Типы данных: double | single
Threshold — Минимальная разность высотМинимальная разность высот между пиком и его соседями в виде разделенной запятой пары, состоящей из 'Threshold' и неотрицательный действительный скаляр. Используйте этот аргумент, чтобы иметь findpeaks возвратите только тот peaks, который превышает их мгновенные соседние значения, по крайней мере, значением 'Threshold'.
Типы данных: double | single
MinPeakDistance — Минимальное пиковое разделениеМинимальное пиковое разделение в виде разделенной запятой пары, состоящей из 'MinPeakDistance' и положительный действительный скаляр. Когда вы задаете значение для 'MinPeakDistance', алгоритм выбирает самый высокий пик в сигнале и игнорирует весь peaks в 'MinPeakDistance' из него. Функция затем повторяет процедуру для самого высокого остающегося пика и выполняет итерации, пока это не исчерпывает peaks, чтобы рассмотреть.
Если вы задаете вектор местоположения, x, затем 'MinPeakDistance' должен быть описан в терминах x. Если x datetime массив, затем задайте 'MinPeakDistance' как duration скаляр или в виде числа описывается в днях.
Если вы задаете частоту дискретизации, Fs, затем 'MinPeakDistance' должен быть описан в модулях времени.
Если вы не задаете никакой x ни Fs, затем 'MinPeakDistance' должен быть описан в модулях выборок.
Используйте этот аргумент, чтобы иметь findpeaks проигнорируйте маленький peaks, который происходит в окружении более крупного пика.
Типы данных: double | single | duration
WidthReference — Ссылочная высота для измерений ширины'halfprom' (значение по умолчанию) | 'halfheight'Ссылочная высота для измерений ширины в виде разделенной запятой пары, состоящей из 'WidthReference' и любой 'halfprom' или 'halfheight'. findpeaks оценивает ширину пика как расстояние между точками, где убывающий сигнал прерывает горизонтальную ссылочную линию. Высота линии выбрана с помощью критерия, заданного в 'WidthReference':
'halfprom' располагает ссылочную линию ниже пика на вертикальном расстоянии, равном половине пикового выдающегося положения. Смотрите Выдающееся положение для получения дополнительной информации.
'halfheight' располагает ссылочную линию в половине пиковой высоты. Линия является усеченной, если какая-либо из ее точек пересечения лежит за пределами границ peaks, выбранного установкой 'MinPeakHeight', 'MinPeakProminence', и 'Threshold'. Граница между peaks задана горизонтальным положением самого низкого оврага между ними. Peaks с высотой меньше, чем нуль отбрасывается.
Местоположения точек пересечения вычисляются линейной интерполяцией.
MinPeakWidth — Минимальная пиковая ширинаМинимальная пиковая ширина в виде разделенной запятой пары, состоящей из 'MinPeakWidth' и положительный действительный скаляр. Используйте этот аргумент, чтобы выбрать только тот peaks, который имеет ширины, по крайней мере, 'MinPeakWidth'.
Если вы задаете вектор местоположения, x, затем 'MinPeakWidth' должен быть описан в терминах x. Если x datetime массив, затем задайте 'MinPeakWidth' как duration скаляр или в виде числа описывается в днях.
Если вы задаете частоту дискретизации, Fs, затем 'MinPeakWidth' должен быть описан в модулях времени.
Если вы не задаете никакой x ни Fs, затем 'MinPeakWidth' должен быть описан в модулях выборок.
Типы данных: double | single | duration
MaxPeakWidth — Максимальная пиковая ширинаInf (значение по умолчанию) | положительный действительный скалярМаксимальная пиковая ширина в виде разделенной запятой пары, состоящей из 'MaxPeakWidth' и положительный действительный скаляр. Используйте этот аргумент, чтобы выбрать только тот peaks, который имеет ширины в большей части 'MaxPeakWidth'.
Если вы задаете вектор местоположения, x, затем 'MaxPeakWidth' должен быть описан в терминах x. Если x datetime массив, затем задайте 'MaxPeakWidth' как duration скаляр или в виде числа описывается в днях.
Если вы задаете частоту дискретизации, Fs, затем 'MaxPeakWidth' должен быть описан в модулях времени.
Если вы не задаете никакой x ни Fs, затем 'MaxPeakWidth' должен быть описан в модулях выборок.
Типы данных: double | single | duration
Annotate — Стиль графика'peaks' (значение по умолчанию) | 'extents'Стиль графика в виде разделенной запятой пары, состоящей из 'Annotate' и одно из этих значений:
'peaks' строит сигнал и аннотирует местоположение и значение каждого пика.
'extents' строит сигнал и аннотирует местоположение, значение, ширину и выдающееся положение каждого пика.
Этот аргумент проигнорирован, если вы вызываете findpeaks с выходными аргументами.
pks — Локальные максимумыЛокальные максимумы, возвращенные как вектор из значений сигналов. Если нет никаких локальных максимумов, то pks isempty.
locs — Пиковые местоположенияПиковые местоположения, возвращенные как вектор.
Если вы задаете вектор местоположения, x, затем locs содержит значения x в пиковых индексах.
Если вы задаете частоту дискретизации, Fs, затем locs числовой вектор моментов времени с разницей во времени 1/Fs между последовательными выборками.
Если вы не задаете никакой x ни Fs, затем locs вектор из целочисленных индексов.
w — Пиковые шириныПиковые ширины, возвращенные как вектор из вещественных чисел. Ширина каждого пика вычисляется как расстояние между точками налево и правом пика, где сигнал прерывает ссылочную линию, высота которой задана WidthReference. Сами точки найдены линейной интерполяцией.
p — Пиковые выдающиеся положенияПиковые выдающиеся положения, возвращенные как вектор из вещественных чисел. Выдающееся положение пика является минимальным вертикальным расстоянием, что сигнал должен убывать по обе стороны от пика прежде или поднимающийся назад на уровень выше, чем пик или достигающий конечной точки. Смотрите Выдающееся положение для получения дополнительной информации.
Выдающееся положение пика измеряется, насколько пик выделяется из-за его внутренней высоты и его местоположения относительно другого peaks. Низкий изолированный пик может быть более видным, чем тот, который выше, но является в противном случае обыкновенным членом высокой области значений.
Измерять выдающееся положение пика:
Поместите маркер в пик.
Расширьте горизонтальную линию от пика налево и прямо пока линия не выполнит одно из следующих действий:
Пересекает сигнал, потому что существует более высокий пик
Достигает левого или правого конца сигнала
Найдите минимум сигнала в каждом из этих двух интервалов заданным на Шаге 2. Эта точка является или оврагом или одной из конечных точек сигнала.
Выше двух минимумов интервала задает контрольный уровень. Высота пика выше этого уровня является своим выдающимся положением.
findpeaks не делает предположения о поведении сигнала вне его конечных точек, безотносительно их высоты. Это отражается на Шагах 2 и 4 и часто влияет на значение контрольного уровня. Рассмотрите, например, peaks этого сигнала:
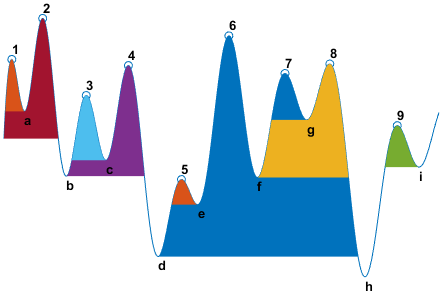
| Пиковый номер | Оставленный интервал находится между пиком и | Правильный интервал находится между пиком и | Самая низкая точка на левом интервале | Самая низкая точка на правильном интервале | Контрольный уровень (самый высокий минимум) |
|---|---|---|---|---|---|
| 1 | Оставленный конец | Пересечение должного достигнуть максимума 2 | Оставленная конечная точка | a | a |
| 2 | Оставленный конец | Правильный конец | Оставленная конечная точка | h | Оставленная конечная точка |
| 3 | Пересечение должного достигнуть максимума 2 | Пересечение должного достигнуть максимума 4 | b | c | c |
| 4 | Пересечение должного достигнуть максимума 2 | Пересечение должного достигнуть максимума 6 | b | d | b |
| 5 | Пересечение должного достигнуть максимума 4 | Пересечение должного достигнуть максимума 6 | d | e | e |
| 6 | Пересечение должного достигнуть максимума 2 | Правильный конец | d | h | d |
| 7 | Пересечение должного достигнуть максимума 6 | Пересечение должного достигнуть максимума 8 | f | g | g |
| 8 | Пересечение должного достигнуть максимума 6 | Правильный конец | f | h | f |
| 9 | Пересечение должного достигнуть максимума 8 | Пересечение из-за правильной конечной точки | h | i | i |
fminbnd | fminsearch | fzero | islocalmax | islocalmin | max
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.