Линеаризация является линейной аппроксимацией нелинейной системы, которая допустима в небольшой области вокруг рабочей точки.
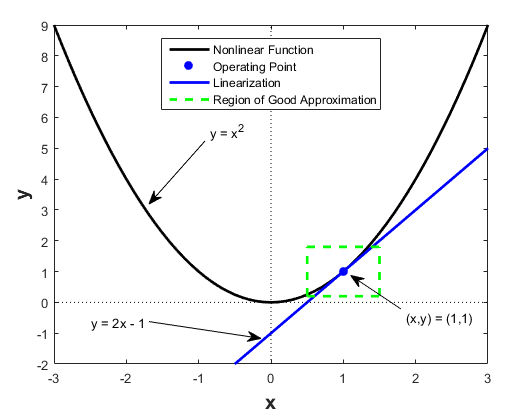
Например, предположите, что нелинейная функция . Линеаризуя эту нелинейную функцию о рабочей точке x = 1, y = 1 результат в линейной функции .
Около рабочей точки, хорошее приближение к . Далеко от рабочей точки, приближение плохо.
Следующий рисунок показывает возможную область хорошего приближения для линеаризации . Фактическая область валидности зависит от нелинейной модели.
Расширяя концепцию линеаризации к динамическим системам, можно написать непрерывному времени нелинейные дифференциальные уравнения в этой форме:
В этих уравнениях x (t) представляет системные состояния, u (t) представляет входные параметры системе, и y (t) представляет выходные параметры системы.
Линеаризовавшая модель этой системы допустима в небольшой области вокруг рабочей точки t=t0, x (t0) =x0, u (t0) =u0, и y (t0) =g (x0, u0, t0) =y0.
Чтобы представлять линеаризовавшую модель, задайте новые переменные, сосредоточенные о рабочей точке:
Линеаризовавшая модель в терминах δx, δu, и δy допустима, когда значения этих переменных малы:
Линеаризация полезна в приложениях системы управления и анализе модели.
Точная линеаризация заданного нелинейного Simulink® модель производит линейное пространство состояний, передаточную функцию или уравнения нулей, полюсов и усиления, для которых можно использовать:
Постройте Предвещать ответ модели Simulink.
Оцените запасы устойчивости цикла путем вычисления ответа разомкнутого контура.
Анализируйте и сравните ответ объекта около различных рабочих точек.
Спроектируйте линейный контроллер
Классические методологии анализа и проектирования системы управления требуют линейных, независимых от времени моделей. Simulink Control Design™ автоматически линеаризует объект, когда вы настраиваете свой компенсатор. Смотрите Выбирают Подход Системы управления.
Анализируйте устойчивость с обратной связью.
Измерьте размер резонансов в частотной характеристике путем вычисления линейной модели с обратной связью для системы управления.
Сгенерируйте контроллеры с уменьшаемой чувствительностью к изменениям параметра и ошибкам моделирования.
Можно использовать программное обеспечение Simulink Control Design, чтобы линеаризовать непрерывное время, дискретное время или многоскоростные модели Simulink. Получившаяся линейная независимая от времени модель находится в форме пространства состояний.
По умолчанию Simulink Control Design линеаризует модели с помощью подхода блока блоком. Этот подход блока блоком индивидуально линеаризует каждый блок в вашей модели Simulink и комбинирует результаты произвести линеаризацию заданной системы.
Можно также линеаризовать систему с помощью полной модели числовое возмущение, где программное обеспечение вычисляет линеаризацию полной модели путем беспокойства значений входных параметров корневого уровня и состояний. Для каждого входа и состояния, программное обеспечение тревожит модель небольшим количеством и вычисляет линейное основанное на модели на ответе модели на эти возмущения. Можно встревожить модель с помощью или правых разностей или центральных различий.
Подход линеаризации блока блоком имеет несколько преимуществ для полной модели числовое возмущение:
Большинство блоков Simulink имеет предварительно запрограммированную линеаризацию, которая обеспечивает точную линеаризацию блока.
Можно использовать линейные аналитические точки, чтобы задать фрагмент модели, чтобы линеаризовать.
Можно сконфигурировать блоки, чтобы использовать пользовательскую линеаризацию, не влияя симуляцию модели.
Структурно неминимальные состояния автоматически удалены.
Можно задать линеаризацию, которая включает неопределенность (требует программного обеспечения Robust Control Toolbox™).
Можно получить подробную диагностическую информацию.
При линеаризации многоскоростных моделей можно использовать различные методы преобразования уровня. Числовое возмущение полное модели может только использовать нулевой порядок "преобразования уровня, содержат".
Точная линеаризация поддерживает большинство блоков Simulink.
Однако блоки Simulink с сильными разрывами или основанной на событии динамикой линеаризуют (правильно), чтобы обнулить или большое (бесконечное) усиление. Модели, которые включают основанное на событии или прерывистое поведение, требуют специальной обработки программным обеспечением Simulink Control Design. Такое основанное на событии или прерывистое поведение может прибыть из блоков, таких как:
Блоки из библиотеки Discontinuities
Stateflow® графики
Триггируемые подсистемы
Сигналы модуляции ширины импульса (PWM)
Для большинства приложений состояния в вашей модели Simulink должны быть в устойчивом состоянии. В противном случае ваша линейная модель только допустима по маленькому временному интервалу.
Выбор правильной рабочей точки для линеаризации очень важен для получения точной линейной модели. Линейная модель является приближением нелинейной модели, которая допустима только около рабочей точки, в которой вы линеаризуете модель.
Несмотря на то, что вы задаете который блоки Simulink линеаризовать, все блоки во влиянии модели рабочая точка.
Нелинейная модель может иметь две совсем других линейных аппроксимации, когда вы линеаризуете о различных рабочих точках.
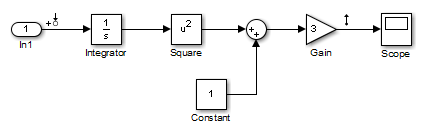
Результат линеаризации для этой модели показывают затем с начальным условием для интегрирования x 0 = 0.

Эта таблица суммирует различные результаты линеаризации для двух различных рабочих точек.
| Рабочая точка | Результат линеаризации |
|---|---|
Начальное условие = 5, x1 состояния | 30/с |
Начальное условие = 0, x1 состояния | 0 |
Можно линеаризовать модель Simulink в трех различных типах рабочих точек:
Обрезанная рабочая точка — Линеаризует в Обрезанной Рабочей точке
Снимок состояния симуляции — Линеаризует в Снимке состояния Симуляции
Инициированное событие симуляции — Линеаризует в Инициированных Событиях Симуляции