График является набором узлов и краев, который представляет отношения:
Узлы являются вершинами, которые соответствуют объектам.
Края являются связями между объектами.
Края графика иногда имеют Веса, которые указывают на силу (или некоторый другой атрибут) каждой связи между узлами.
Эти определения являются общими, когда точное значение узлов и краев в графике зависит от определенного приложения. Например, можно смоделировать дружбу в социальной сети с помощью графика. Вершины графика являются людьми, и края представляют дружбу. Естественное соответствие графиков к физическим объектам и ситуациям означает, что можно использовать графики, чтобы смоделировать большое разнообразие систем. Например:
Веб-страница, соединяющаяся — вершины графика являются веб-страницами, и края представляют гиперссылки между страницами.
Аэропорты — Вершины графика являются аэропортами, и края представляют полеты между аэропортами.
В MATLAB®, graph и digraph функционирует объекты построения, которые представляют неориентированных и ориентированных графов.
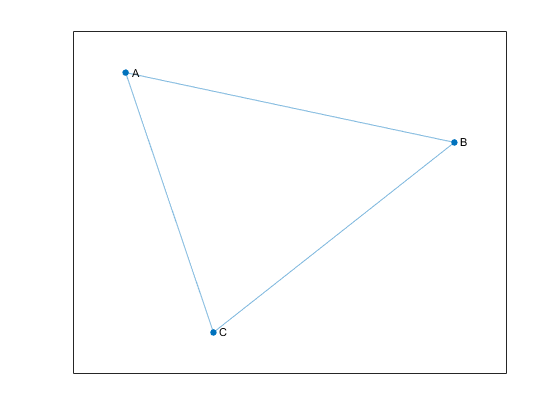
Неориентированные графы имеют края, которые не имеют направления. Края указывают на двухстороннее отношение, в котором каждый край может быть пересечен в обоих направлениях. Эти данные показывают простого неориентированного графа с тремя узлами и тремя краями.
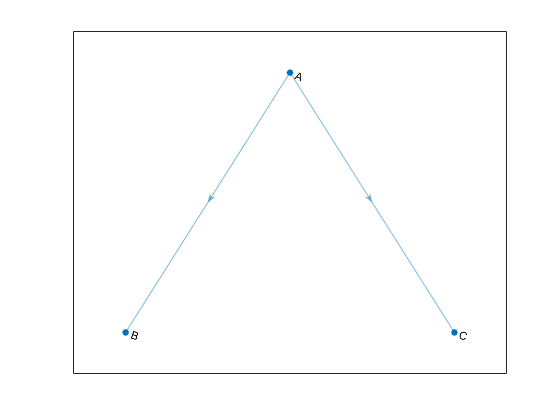
Ориентированные графы имеют края с направлением. Края указывают на одностороннее отношение, в котором каждый край может только быть пересечен в единственном направлении. Эти данные показывают простого ориентированного графа с тремя узлами и двумя краями.
Точное положение, длина или ориентация краев на иллюстрации графика обычно не имеют значения. Другими словами, тот же график может визуализироваться несколькими различными способами путем реконструкции узлов и/или искажения краев, пока глубинная структура не изменяется.
Графики, созданные с помощью graph и digraph, могут иметь один или несколько самоциклов, которые являются краями, соединяющими узел с собой. Кроме того, графики могут иметь несколько краев с теми же входными и выходными узлами, и график затем известен как мультиграф. Мультиграф может или не может содержать самоциклы.
В целях функций алгоритма графика в MATLAB график, содержащий узел с единственным самоциклом, не является мультиграфом. Однако, если график содержит узел с несколькими самоциклами, это - мультиграф.
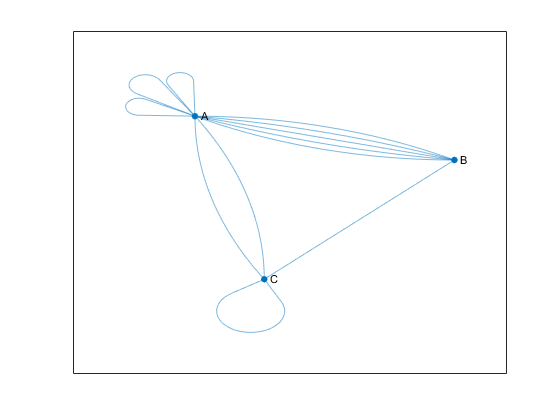
Например, следующие данные показывают неориентированный мультиграф с самоциклами. Узел A имеет три самоцикла, в то время как узел C имеет тот. График содержит эти три условия, любое из которых делает его мультиграфом.
Узел A имеет три самоцикла.
Узлы A и B имеют пять краев между ними.
Узлы A и C имеют два края между ними.
Чтобы определить, является ли данный график мультиграфом, используйте функцию ismultigraph.
Первичные способы создать график включают использование матрицы смежности или списка краев.
Один способ представлять информацию в графике с квадратной матрицей смежности. Ненулевые записи в матрице смежности указывают на край между двумя узлами, и значение записи указывает на вес края. Диагональные элементы матрицы смежности обычно являются нулем, но ненулевой диагональный элемент указывает на самоцикл или узел, который соединяется с собой краем.
Когда вы используете graph, чтобы создать неориентированного графа, матрица смежности должна быть симметричной. На практике матрицы являются часто треугольными, чтобы избежать повторения. Чтобы создать неориентированного графа с помощью только верхний или более низкий треугольник матрицы смежности, используйте graph(A,'upper') или graph(A,'lower').
Когда вы используете digraph, чтобы создать ориентированного графа, матрица смежности не должна быть симметричной.
Для больших графиков матрица смежности содержит много нулей и обычно является разреженной матрицей.
Вы не можете создать мультиграф из матрицы смежности.
Например, рассмотрите этого неориентированного графа.
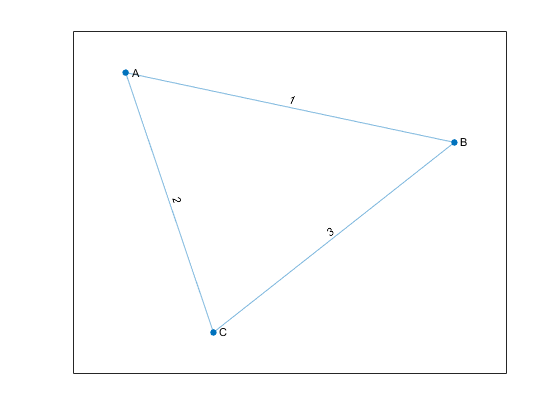
Можно представлять график с этой матрицей смежности:
Чтобы создать график в MATLAB, введите:
A = [0 1 2; 1 0 3; 2 3 0];
node_names = {'A','B','C'};
G = graph(A,node_names)G =
graph with properties:
Edges: [3×2 table]
Nodes: [3×1 table]Можно использовать graph или функции digraph, чтобы создать график с помощью матрицы смежности, или вы можете использовать функцию adjacency, чтобы найти взвешенное или облегчили разреженную матрицу смежности существующего ранее графика.
Другой способ представлять информацию в графике путем листинга всех краев.
Например, рассмотрите того же неориентированного графа.

Теперь представляйте график списком краев
Из списка краев легко прийти к заключению, что график имеет три уникальных узла, A, B и C, которые соединяются тремя перечисленными краями. Если бы график отключил узлы, они не были бы найдены в списке краев и должны были бы быть заданы отдельно.
В MATLAB список краев разделяется столбцом в исходные узлы и целевые узлы. Для ориентированных графов граничное направление (из источника, чтобы предназначаться) важно, но для неориентированных графов входной и выходной узел является взаимозаменяемым. Один способ создать этот график с помощью списка краев состоит в том, чтобы использовать отдельные входные параметры для исходных узлов, целевых узлов и веса ребра:
source_nodes = {'A','A','B'};
target_nodes = {'B','C','C'};
edge_weights = [1 2 3];
G = graph(source_nodes, target_nodes, edge_weights);И graph и digraph разрешают конструкцию простого графика или мультиграфа из списка краев. После построения графика, G, можно посмотреть на края (и их свойства) с командой G.Edges Края. Порядок краев в G.Edges сортируется по исходному узлу (первый столбец) и во вторую очередь по целевому узлу (второй столбец). Для неориентированных графов узел с меньшим индексом перечислен как исходный узел, и узел с большим индексом перечислен как целевой узел.
Поскольку конкретная реализация graph и digraph зависит от разреженных матриц, многие из тех же затрат на индексацию применяются. Используя один из предыдущих методов, чтобы создать график целиком из пар триплета (source,target,weight) более быстр, чем создание пустого графика и многократно добавление большего количества узлов и краев. Для лучшей производительности минимизируйте количество вызовов graph, digraph, addedge, addnode, rmedge и rmnode.
По умолчанию все узлы в графике, созданном с помощью graph или digraph, пронумерованы. Поэтому всегда можно обращаться к ним их числовым индексом узла.
Если график имеет имена узла (то есть, G.Nodes содержит переменный Name), то также можно обратиться к узлам в графике с помощью их имен. Таким образом, названный узлами в графике может быть упомянут или их индексами узла или именами узла. Например, узел 1 может быть назван, 'A'.
Термин идентификатор узла охватывает оба аспекта идентификации узла. Идентификатор узла относится к индексу узла и к имени узла.
Для удобства MATLAB помнит, какой тип идентификатора узла вы используете, когда вы вызываете большинство функций графика. Таким образом, если вы обращаетесь к узлам в графике их индексами узла, большинство функций графика дает числовой ответ, который также относится к узлам их индексами.
A = [0 1 1 0; 1 0 1 0; 1 1 0 1; 0 0 1 0];
G = graph(A,{'a','b','c','d'});
p = shortestpath(G,1,4)
p =
1 3 4
Однако, если вы обращаетесь к узлам их именами, затем большинство функций графика дает ответ, который также относится к узлам их именами (содержавшийся в массиве ячеек из символьных векторов или массиве строк).
p1 = shortestpath(G,'a','d')
p1 =
1×3 cell array
{'a'} {'c'} {'d'}Используйте findnode, чтобы найти числовой идентификатор узла для данного имени узла. С другой стороны, для данного числового идентификатора узла, индексируйте в G.Nodes.Name, чтобы определить соответствующее имя узла.
После того, как вы создаете объект graph или digraph, можно использовать множество функций, чтобы изменить структуру графика или определить, сколько узлов или ограничивается, график имеет. Эта таблица приводит некоторые доступные функции для изменения или запроса объекты digraph и graph.
addedge | Добавьте один или несколько краев к графику |
rmedge | Удалите один или несколько краев из графика |
addnode | Добавьте один или несколько узлов к графику |
rmnode | Удалите один или несколько узлов из графика |
findnode | Найдите определенный узел в графике |
findedge | Найдите определенный край в графике |
numNodes | Найдите количество узлов в графике |
numedges | Найдите количество краев в графике |
edgecount | Количество краев между заданными узлами |
flipedge | Инвертируйте направление краев ориентированного графа |
reordernodes | Переставьте порядок узлов в графике |
подграф | Извлечение подграфа |
Смотрите Изменяют Узлы и Края Существующего графика для некоторых общих примеров модификации графика.