(Не рекомендуемый) Простой в использовании 3-D цветной поверхностный плоттер
ezsurf не рекомендуется. Используйте fsurf вместо этого.
ezsurf (fun)
ezsurf (fun, область)
ezsurf (funx, funy, funz)
ezsurf (funx, funy, funz, [smin, smax, tmin, tmax])
ezsurf (funx, funy, funz, [min, макс.])
ezsurf... N
ezsurf..., 'циркуляция')
ezsurf (axes_handle...)
h = ezsurf (...)
ezsurf(fun) создает график fun(x,y) с помощью функции surf. fun построен график по области по умолчанию:-2π <x <2π,-2π <y <2π.
fun может быть указателем на функцию, вектором символа или строкой (см. раздел Tips).
ezsurf(fun,domain) строит график fun по заданному domain. domain должен быть вектором. Смотрите, что раздел Algorithms для получения дополнительной информации о векторных входных параметрах по сравнению с осями ограничивает выходные параметры.
ezsurf(funx,funy,funz) строит график параметрического поверхностного funx(s,t), funy(s,t) и funz(s,t) по квадрату:-2π <s <2π,-2π <t <2π.
ezsurf(funx,funy,funz,[smin,smax,tmin,tmax]) или ezsurf(funx,funy,funz,[min,max]) строят график параметрической поверхности с помощью заданной области.
ezsurf..., n) строит график fun по области по умолчанию с помощью n на n сетки. Значение по умолчанию для n равняется 60.
ezsurf..., 'циркуляция'), строит график fun по диску, центрируемому на области.
ezsurf(axes_handle,...) строит график в оси с указателем axes_handle вместо текущей системы координат (gca).
h = ezsurf(...) возвращает указатель на объект подложки в h.
Постройте график функции
по области
и
. Функция ezsurf не строит график точек, где математическая функция не задана. Эти точки установлены в NaN так, чтобы они не строили график.
figure
ezsurf('real(atan(x+i*y))')
Используйте surf, чтобы отобразить те же данные на графике, не фильтруя разрывы.
figure [x,y] = meshgrid(linspace(-2*pi,2*pi,60)); z = real(atan(x+1i.*y)); surf(x,y,z)
ezsurf и ezsurfc не принимают комплексные входные параметры.
Умножение массивов, деление и возведение в степень всегда подразумеваются в выражении, которое вы передаете ezsurf. Например, синтаксис MATLAB® для объемной поверхностной диаграммы выражения
sqrt(x.^2 + y.^2);
записан как
ezsurf('sqrt(x^2 + y^2)')Таким образом, x^2 интерпретирован как x.^2 в векторе символа, или представьте вас в виде строки, передают ezsurf.
Если функция, которая будет построена график, является функцией переменных u и v (а не x и y), то доменные конечные точки umin, umax, vmin и vmax сортируются в алфавитном порядке. Таким образом ezsurf('u^2 - v^3',[0,1],[3,6]) строит график u2 - v3 более чем 0 <u <1, 3 <v <6.
Аргументы указателя на функцию должны указать на функции тому использованию синтаксис MATLAB. Например, следующие операторы задают анонимную функцию и передают указатель на функцию fh ezsurf.
fh = @(x,y) sqrt(x.^2 + y.^2); ezsurf(fh)
Обратите внимание на то, что при использовании указателей на функцию, необходимо использовать степень массивов, умножение массивов и операторы деления массивов (.^, .*, ./), поскольку ezsurf не изменяет синтаксис, как в случае с вектором символа или представляет входные параметры в виде строки.
Если ваша функция имеет дополнительные параметры, например k в myfun:
function z = myfun(x,y,k1,k2,k3) z = x.*(y.^k1)./(x.^k2 + y.^k3);
затем можно использовать анонимную функцию, чтобы указать что параметр:
ezsurf(@(x,y)myfun(x,y,2,2,4))
ezsurf определяет x-и пределы осей Y по-разному в зависимости от того, как вы вводите область (если вообще). В следующей таблице R является вектором [xmin, xmax, ymin, ymax] и v являются вручную вводимым доменным вектором.
| Количество значений домена задало: | Получившийся доменный вектор: |
|---|---|
v = [ ]; |
R = [-2*pi, 2*pi, -2*pi, 2*pi]; |
v = [ v(1) ]; |
R = double([-abs(v),abs(v),-abs(v),abs(v)]); |
v = [ v(1) v(2) ]; |
R = double([v(1),v(2),v(1),v(2)]); |
v = [ v(1) v(2) v(3) ]; |
R = double([-v(1),v(2),-abs(v(3)),abs(v(3))]); |
v = [ v(1) v(2) v(3) v(4) ]; |
R = double(v); |
v = [ v(1)..v(n) ]; n>4 |
R = double([-abs(v(1)), abs(v(1)), -abs(v(1)), abs(v(1))]); |
Если вы задаете единственный номер в невекторном формате (без квадратных скобок, []), ezsurf интерпретирует его как n, число точек, желаемое между осями значения min и max.
По умолчанию ezsurf использует 60 точек между max и значениями min оси. Когда min и значения max являются значениями по умолчанию (R = [-2*pi, 2*pi, -2*pi, 2*pi];), ezsurf гарантирует, чтобы 60 точек находились в пределах некомплексной области значений заданного уравнения. Например, только действительно когда . График по умолчанию этой функции выглядит так:
ezsurf('sqrt(1-x^2-y^2)')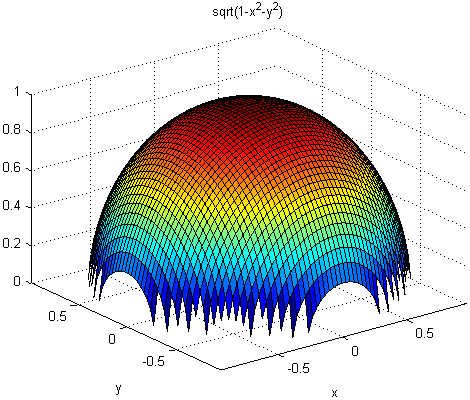
Вы видите, что существует 60 точек между минимальными и максимальными значениями для который 1−x2−y2has действительные значения. Однако, когда вы задаете значения домена, чтобы совпасть со значением по умолчанию (R = [-2*pi, 2*pi, -2*pi, 2*pi];), различный результат появляется:
ezsurf('sqrt(1-x^2-y^2)',[-2*pi 2*pi])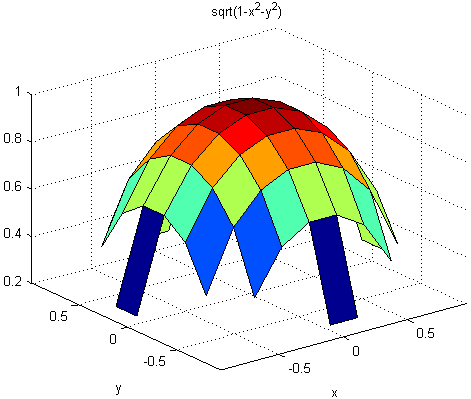
В этом случае графические пределы являются тем же самым, но ezsurf использовал 60 точек между пользовательскими пределами вместо того, чтобы проверить, чтобы видеть, будут ли все те точки иметь действительные ответы.