Exponenta Banner

allmargin

Получите поле, поле фазы, задержите поле и перекрестно соедините частоты

свернуть все на странице

Синтаксис

S = allmargin(L)
S = allmargin(mag,phase,w,ts)

Описание

пример

S = allmargin(L) вычисляет поле усиления, поле фазы, поле задержки и соответствующие перекрестные частоты для SISO или цикла отрицательной обратной связи MIMO с ответом разомкнутого цикла L. Цикл отрицательной обратной связи вычисляется как feedback(L,eye(M)), где M является количеством вводов и выводов в L.

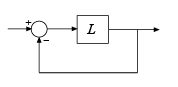
Для системы MIMO allmargin возвращает цикл за один раз запасы устойчивости для системы замкнутого цикла отрицательной обратной связи. Используйте allmargin, чтобы найти классические поля любой модели SISO или MIMO, включая модели с задержками.

пример

S = allmargin(mag,phase,w,ts) вычисляет запасы устойчивости из данных о частотной характеристике mag, phase, w, и шаг расчета, ts.

Примеры

свернуть все

Скрипт Open Live Script

В данном примере считайте передаточную функцию разомкнутого цикла SISO L данный,

L=25s3+10s2+10s+10

L = tf(25,[1 10 10 10]);

Найдите запасы устойчивости L.

S = allmargin(L)
S = struct with fields:
     GainMargin: 3.6000
    GMFrequency: 3.1623
    PhaseMargin: 29.1104
    PMFrequency: 1.7844
    DelayMargin: 0.2847
    DMFrequency: 1.7844
         Stable: 1

Вывод S является структурой с классическими полями и их соответствующими перекрестными частотами цикла отрицательной обратной связи L.

Скрипт Open Live Script

В данном примере считайте модель в пространстве состояний MIMO L с 2 входными параметрами и 2 выходными параметрами.

Загрузите данные.

load('mimoStateSpaceModel.mat','L')

Найдите классические поля для системы MIMO.

S = allmargin(L)
S = 2x1 struct array with fields:
    GainMargin
    GMFrequency
    PhaseMargin
    PMFrequency
    DelayMargin
    DMFrequency
    Stable

Вывод S 2 1 массив структур классических полей и их соответствующих перекрестных частот. Например, S(1) относится к запасам устойчивости первого канала обратной связи ввода-вывода со всеми другими замкнутыми кругами.

Скрипт Open Live Script

В данном примере загрузите invertedPendulumArray.mat, который содержит массив 3х3 инвертированных моделей SISO маятника. Масса маятника отличается, когда вы перемещаетесь от модели до модели вдоль отдельного столбца sys, и длина маятника отличается, когда вы проходите одна строка. Массовые используемые значения составляют 100 г, 200 г и 300 г, и используемые длины маятника составляют 3 м, 2 м и 1 м соответственно.

Column1Column2Column3Row1100g,3m100g,2m100g,1mRow2200g,3m200g,2m200g,1mRow3300g,3m300g,2m300g,1m

load('invertedPendulumArray.mat','sys');
size(sys)
3x3 array of transfer functions.
Each model has 1 outputs and 1 inputs.

Найдите запасы устойчивости для всех моделей в массиве.

S = allmargin(sys)
S = 3x3 struct array with fields:
    GainMargin
    GMFrequency
    PhaseMargin
    PMFrequency
    DelayMargin
    DMFrequency
    Stable

allmargin возвращает 3х3 массив структур S, в котором каждая запись является структурой, содержащей запасы устойчивости соответствующей записи в sys. Например, запасы устойчивости модели с 100-граммовым весом маятника и 2 м длиной содержатся в S(1,2).

Скрипт Open Live Script

В данном примере загрузите данные о частотной характеристике системы разомкнутого цикла, состоя из значений m и значения фазы p, измеренный на частотах в w.

load('openLoopFRData.mat','m','p','w','ts');

Вычислите запасы устойчивости с помощью данных о частотной характеристике.

S = allmargin(m,p,w,ts)
S = struct with fields:
     GainMargin: 0.6249
    GMFrequency: 1.2732
    PhaseMargin: [-90.0000 48.9853]
    PMFrequency: [1.0000 1.5197]
    DelayMargin: [4.7124 0.5626]
    DMFrequency: [1.0000 1.5197]
         Stable: NaN

Вывод S является структурой с классическими полями и их соответствующими перекрестными частотами. Поскольку allmargin не может оценить устойчивость для моделей данных частотной характеристики, S.Stable = NaN.

Входные параметры

свернуть все

Ответ разомкнутого цикла, заданный как модель динамической системы. L может быть SISO или MIMO, пока это имеет то же количество вводов и выводов. allmargin вычисляет классические запасы устойчивости для отрицательной обратной связи система с обратной связью feedback(L,eye(M)):

Чтобы вычислить запасы устойчивости системы позитивных откликов feedback(L,eye(M),+1), используйте allmargin(-L).

Когда у вас есть контроллер P и объект C, можно вычислить запасы устойчивости для усиления и изменений фазы при вводах или выводах объекта. Из следующей схемы:

  • Чтобы вычислить поля на объекте выходные параметры, установите L = P*C.

  • Чтобы вычислить поля во входных параметрах объекта, установите L = C*P.

L может быть непрерывным временем или дискретным временем. Если L является обобщенной моделью в пространстве состояний (genss или uss), то allmargin использует текущее значение или номинальную стоимость всех блоков системы управления в L.

Если L является моделью данных частотной характеристики (такой как frd), то allmargin вычисляет поля на каждой частоте, представленной в модели. Функция возвращает поля на частоте с самым маленьким запасом устойчивости.

Если L является образцовым массивом, то allmargin вычисляет поля для каждой модели в массиве.

Значение отклика системы в абсолютных единицах, заданных как трехмерный массив. mag является M массивом m на n, где M является количеством вводов или выводов, и N является количеством точек частоты. Для получения дополнительной информации о получении mag смотрите, Получают Данные о Значении и Фазе и Значение и Фазу Системы MIMO.

Фаза отклика системы в градусах, заданный как трехмерный массив. phase является M массивом m на n, где M является количеством вводов или выводов, и N является количеством точек частоты. Для получения дополнительной информации о получении phase смотрите, Получают Данные о Значении и Фазе и Значение и Фазу Системы MIMO.

Частоты, на которых получены значение и значения фазы отклика системы, задали как вектор-столбец. Можно предоставить вектору частоты w в любых модулях; allmargin возвращает частоты в тех же модулях. allmargin интерполирует между точками частоты, чтобы аппроксимировать истинные запасы устойчивости.

Шаг расчета, заданный как целое число. allmargin использует ts, чтобы найти запасы устойчивости от данных о частотной характеристике.

  • Для непрерывно-разовых моделей, набор ts = 0.

  • Для моделей дискретного времени ts является положительным целым числом, представляющим период выборки. Чтобы обозначить модель дискретного времени с незаданным шагом расчета, установите ts = -1.

Выходные аргументы

свернуть все

Усиление, фаза, и поля задержки, возвратилось как массив структур.

Вывод S является структурой со следующими полями:

  • GMFrequency: Все-180 ° (360 ° по модулю) перекрестно соединяют частоты в rad/TimeUnit, где TimeUnit является единицами измерения времени, заданными в свойстве TimeUnit L.

  • GainMargin: Соответствующие поля усиления, заданные как 1/G, где G является усилением на перекрестной частоте на-180 °. Поля усиления находятся в абсолютных единицах.

  • PMFrequency: Все перекрестные частоты на 0 дБ в rad/TimeUnit, где TimeUnit является единицами измерения времени, заданными в свойстве TimeUnit L.

  • PhaseMargin: Соответствующие поля фазы в градусах.

  • DMFrequency и DelayMargin: DelayMargin является максимальной суммой задержки, которую может терпеть система, прежде чем это потеряет устойчивость. DMFrequency содержит критические частоты, соответствующие полям задержки. Задержитесь поля заданы в единицах измерения времени системы для непрерывно-разовых систем и множителей шага расчета для систем дискретного времени.

  • Stable: 1, если номинальная система с обратной связью стабильна, 0, если нестабильный и NaN, если устойчивость не может быть оценена. В целом allmargin не может оценить устойчивость системы frd.

Когда L является M-by-M системой MIMO, S является массивом структур M-1. Например, S(j) дает запасы устойчивости для j-th канала обратной связи со всеми другими замкнутыми кругами (один цикл за один раз поля).

Советы

  • allmargin принимает, что система с ответом разомкнутого цикла L является системой отрицательной обратной связи. Чтобы вычислить классические запасы устойчивости системы позитивных откликов feedback(L,eye(M),+1), используйте allmargin(-L).

  • Чтобы вычислить классические поля для системы, смоделированной в Simulink®, сначала линеаризуйте модель, чтобы получить ответ разомкнутого цикла в конкретной рабочей точке. Затем используйте allmargin, чтобы вычислить классические запасы устойчивости для линеаризовавшей системы. Для получения дополнительной информации смотрите Запасы устойчивости Модели Simulink (Robust Control Toolbox).

Смотрите также

| |

Темы

Представлено до R2006a

Документация Control System Toolbox
Поддержка