обратная связь

Связь обратной связи двух моделей

Синтаксис

sys = feedback(sys1,sys2)

Описание

sys = feedback(sys1,sys2) возвращает объект модели sys для соединения отрицательной обратной связи объектов модели sys1 и sys2.

Модель sys с обратной связью имеет u как входной вектор и y как выходной вектор. Модели sys1 и sys2 должны быть оба непрерывными или оба дискретные с идентичными шагами расчета. Правила приоритета использованы, чтобы определить получившийся тип модели (см. Правила, Которые Определяют Тип модели).

Чтобы применить позитивные отклики, используйте синтаксис

sys = feedback(sys1,sys2,+1)

По умолчанию feedback(sys1,sys2) принимает отрицательную обратную связь и эквивалентен feedback(sys1,sys2,-1).

Наконец,

sys = feedback(sys1,sys2,feedin,feedout)

вычисляет модель sys с обратной связью для более общей обратной связи.

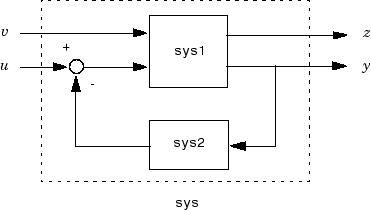
Векторный feedin содержит индексы во входной вектор sys1 и задает, какие входные параметры u вовлечены в обратную связь. Точно так же feedout задает, который выходные параметры y sys1 используются для обратной связи. Получившаяся модель sys имеет те же вводы и выводы как sys1 (с их сохраненным порядком). Как прежде, отрицательная обратная связь применяется по умолчанию, и необходимо использовать

sys = feedback(sys1,sys2,feedin,feedout,+1)

применять позитивные отклики.

Для более сложных структур обратной связи используйте append и connect.

Примеры

Пример 1

Соединять объект

$G (s) = \frac{2 s^{2} + 5 s + 1}{s^{2} + 2 s + 3}$

с контроллером

$H (s) = \frac{5 (s + 2)}{s + 10}$

с помощью отрицательной обратной связи ввести

G = tf([2 5 1],[1 2 3],'inputname','torque',...
                         'outputname','velocity');
H = zpk(-2,-10,5)
Cloop = feedback(G,H)

Эти команды приводят к следующему результату.

Zero/pole/gain from input "torque" to output "velocity":
0.18182 (s+10) (s+2.281) (s+0.2192)
-----------------------------------
 (s+3.419) (s^2 + 1.763s + 1.064)

Результатом является модель нулей и полюсов как ожидалось от правил приоритета. Обратите внимание на то, что Cloop наследовал имена ввода и вывода от G.

Пример 2

Считайте объект пространства состояний P с пятью входными параметрами и четырьмя выходными параметрами и контроллером обратной связи пространства состояний K с тремя входными параметрами и двумя выходными параметрами.

P = rss(3,4,5);
K = rss(3,2,3);

Соединять выходные параметры 1, 3, и 4 из объекта к входным параметрам контроллера и контроллер выходные параметры к входным параметрам 4 и 2 из объекта, использования

feedin = [4 2];
feedout = [1 3 4];
Cloop = feedback(P,K,feedin,feedout)

Пример 3

Можно сформировать следующие циклы отрицательной обратной связи

Cloop = feedback(G,1)       % left diagram
Cloop = feedback(1,G)      % right diagram

Ограничения

Связь обратной связи должна быть свободна от алгебраического цикла. Если _D1 и _D2 являются проходными матрицами sys1 и sys2, это условие эквивалентно:

_{I + D1D2}, несингулярный при использовании отрицательной обратной связи
_{I − D1D2}, несингулярный при использовании позитивных откликов.

Смотрите также

connect | parallel | series

Документация