Документация

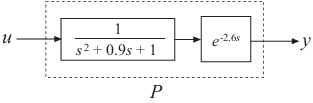
Создайте демонстрационную систему разомкнутого цикла с выходной задержкой.

s = tf('s');
P = exp(-2.6*s)/(s^2+0.9*s+1);

P является объектом (tf) передаточной функции второго порядка с задержкой.

Вычислите приближение Padé первого порядка P.

Pnd1 = pade(P,1)

Pnd1 =
 
             -s + 0.7692
  ----------------------------------
  s^3 + 1.669 s^2 + 1.692 s + 0.7692
 
Continuous-time transfer function.

Эта команда заменяет все задержки P с приближением первого порядка. Поэтому Pnd1 является передаточной функцией третьего порядка без задержек.

Сравните частотную характеристику исходных и аппроксимированных моделей с помощью bodeplot.

h = bodeoptions;
h.PhaseMatching = 'on';
bodeplot(P,'-b',Pnd1,'-.r',{0.1,10},h)
legend('Exact delay','First-Order Pade','Location','SouthWest')

Значение P и Pnd1 соответствует точно. Однако фаза Pnd1 отклоняется от фазы P вне приблизительно 1 рад/с.

Увеличьте порядок приближения Padé расширить диапазон частот, в котором приближение фазы хорошо.

Pnd3 = pade(P,3);

Сравните частотную характеристику P, Pnd1 и Pnd3.

bodeplot(P,'-b',Pnd3,'-.r',Pnd1,':k',{0.1 10},h)
legend('Exact delay','Third-Order Pade','First-Order Pade',...
       'Location','SouthWest')

Ошибка приближения фазы уменьшается при помощи третьего порядка приближение Padé.

Сравните ответы области времени исходных и аппроксимированных систем с помощью stepplot.

stepplot(P,'-b',Pnd3,'-.r',Pnd1,':k')
legend('Exact delay','Third-Order Pade','First-Order Pade',...
       'Location','Southeast')

Используя Padé приближение вводит неминимальный артефакт фазы (“неправильный путь” эффект) в начальном переходном ответе. Эффект вполне объявлен в приближении первого порядка, которое опускается значительно ниже нуля прежде, чем изменить направление. Эффект уменьшается в приближении высшего порядка, которое намного более тесно совпадает с ответом точной системы.