Построение и Работа со Сплайнами ppform

Построение ppform

Кусочный полином обычно создается некоторой командой, посредством процесса интерполяции или приближения или преобразования из некоторой другой формы, например, из B-формы, и выводится как переменная. Но также возможно составить то с нуля, с помощью оператора

pp
= ppmak(breaks,coefs)

Например, если вы вводите pp=ppmak(-5:-1,-22:-11), или, более явным образом,

breaks = -5:-1;
coefs = -22:-11; pp = ppmak(breaks,coefs);

вы задаете универсальную последовательность пропуска-5:-1 и содействующую последовательность-22:-11. Поскольку эта последовательность пропуска имеет 5 записей, следовательно 4 разбивают интервалы, в то время как содействующая последовательность имеет 12 записей, вы, в действительности, задали кусочный полином порядка 3 (= 12/4). Команда

fnbrk(pp)

распечатывает все составные части этого кусочного полинома, можно следующим образом:

breaks(1:l+1)
    -5 -4 -3 -2 -1  
coefficients(d*l,k)
     -22 -21 -20
     -19 -18 -17
     -16 -15 -14 
     -13 -12 -11
  pieces number l
    4 
order k 
  3 
dimension d of target
    1

Далее, fnbrk может использоваться, чтобы предоставить каждую из этих частей отдельно. Но точка функциональности сплайна Curve Fitting Toolbox™ - то, что вы обычно не должны интересоваться этими деталями. Вы просто используете pp в качестве аргумента к командам, которые оценивают, дифференцируют, интегрируют, преобразовывают или строят кусочный полином, описание которого содержится в pp.

Работа Со Сплайнами ppform

Вот некоторые функции для операций, которые можно выполнить на кусочном полиноме.

`v = fnval(pp,x)`	Оценивает
`dpp = fnder(pp)`	Дифференцируется
`dirpp = fndir(pp,dir)`	Дифференцирует в направлении `dir`
`ipp = fnint(pp)`	Объединяется
`fnmin(pp,[a,b])`	Находит минимальное значение в данном интервале
`fnzeros(pp,[a,b])`	Находит нули в данном интервале
`pj = fnbrk(pp,j)`	Вытаскивает `j` th полиномиальная часть
`pc = fnbrk(pp,[a b])`	Ограничивает/расширяет интервалом [`a`.. `b`
`po = fnxtr(pp,order)`	Расширяет вне его основного интервала полиномом заданного порядка
`fnplt(pp,[a,b])`	Графики на данном интервале
`sp = fn2fm(pp,'B-')`	Преобразовывает в B-форму
`pr = fnrfn(pp,morebreaks)`	Вставляет дополнительные пропуски

Вставка дополнительных пропусков пригождается когда это необходимо, чтобы добавить два кусочных полинома с различными пропусками, как сделан в команде fncmb.

ppform в качестве примера

Выполните следующие команды, чтобы создать и построить конкретный кусочный полином (ppform), описанная в Построении раздела ppform.

Создайте кусочный полином с последовательностью пропуска -5:-1 и содействующая последовательность -22:-11:
```
pp=ppmak(-5:-1,-22:-11)
```

Создайте основной график:

x = linspace(-5.5,-.5,101);
plot(x, fnval(pp,x),'x')

Добавьте строки пропуска в график:

breaks=fnbrk(pp,'b'); yy=axis; hold on
for j=1:fnbrk(pp,'l')+1
   plot(breaks([j j]),yy(3:4))
end

Наложите график полинома, который предоставляет третью полиномиальную часть:
```
plot(x,fnval(fnbrk(pp,3),x),'linew',1.3)
set(gca,'ylim',[-60 -10]), hold off 
```

Функция кусочного полинома, ее пропуски и полином, дающий ее третью часть

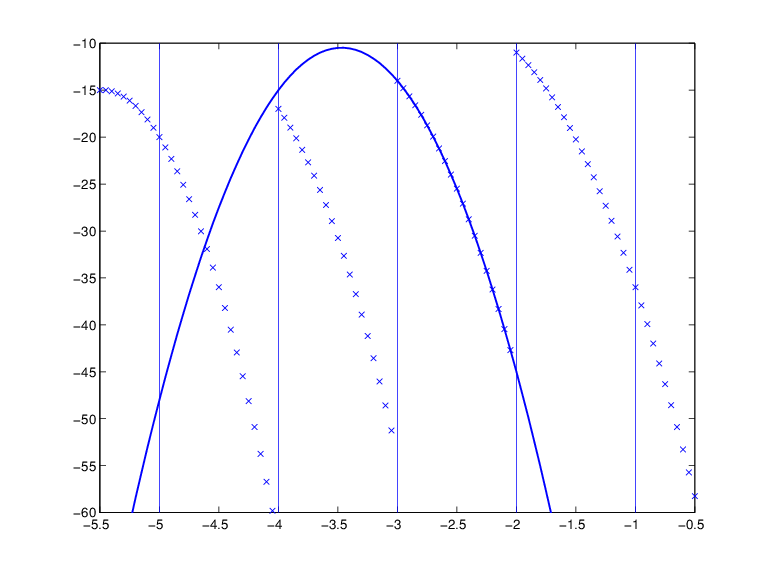
Фигура выше является конечным изображением. Это показывает кусочный полином последовательностью точек и, единогласно сверху его, полинома, из которого взята его третья полиномиальная часть. Довольно примечательно, что значение кусочного полинома в пропуске является своим пределом справа, и что значение кусочного полинома вне его основного интервала получено путем расширения ее крайнего левого, соответственно его самая правая, полиномиальная часть.

В то время как ppform кусочного полинома эффективна для оценки, конструкция кусочного полинома от некоторых данных обычно более эффективно обрабатывается путем определения сначала его B-формы, т.е. его представления как линейная комбинация B-сплайнов.

Документация