Сглаживание сплайна
sp = spaps(x,y,tol)
[sp,values] = spaps(x,y,tol)
[sp,values,rho] = spaps(x,y,tol)
[...] = spaps(x,y,tol,arg1,arg2,...)
[...] = spaps({x1,...,xr},y,tol,...)
sp = spaps(x,y,tol) возвращает B-форму самого сглаженного функционального f, который находится в данном допуске, который tol определенных данных указывает (x(j), y(:,j)), j=1:length(x). Значения данных y(:,j) могут быть скалярами, векторами, матрицами, даже массивы ND. Точки данных с тем же сайтом данных заменяются их взвешенным средним с его весом сумма соответствующих весов и допуск, tol уменьшается соответственно.
[sp,values] = spaps(x,y,tol) также возвращает сглаживавшие значения, т.е. values совпадает с fnval(sp,x).
Здесь, расстояние функционального f от определенных данных измеряется
с выбором по умолчанию для весов w, делающий E (f) составное приближение метода трапеций к , и |z|2, обозначающий сумму квадратов записей z.
Далее, самый сглаженный означает, что следующая мера по шероховатости минимизирована:
где Dmf обозначает m th производная f. Значением по умолчанию для m является 2, значение по умолчанию для веса меры по шероховатости, λ является постоянным 1, и это делает f кубическим сплайном сглаживания.
Когда tol является неотрицательным, затем сплайн, f определяется как уникальный минимизатор выражения ρE (f) + F (Dmf) с параметром сглаживания ρ (опционально возвратился), так выбранный, что E (f) равняется tol. Следовательно, когда m является 2, затем, после того, как преобразование в ppform, результатом должно будет быть то же самое (до округления), как получено csaps (x, y, ρ / (ρ + 1)). Далее, когда tol является нулем, затем “естественный” или вариационный сплайн interpolant порядка 2m возвращен. Для достаточно большого tol приближения наименьших квадратов к данным полиномами степени <возвращен m.
Когда tol отрицателен, затем ρ взят, чтобы быть -tol.
Значение по умолчанию для функции веса λ в мере по шероховатости является постоянной функцией 1. Но можно выбрать его, чтобы быть, в более общем плане, кусочной постоянной функцией, с пропусками только на сайтах данных. Принимая векторный x, чтобы строго увеличиться, вы задаете такой кусочный постоянный λ путем введения tol как вектора, одного размера как x. В этом случае tol(i) взят в качестве постоянного значения λ на интервале (x(i-1).. x(i)), i=2:length(x), в то время как tol(1) продолжает использоваться в качестве заданного допуска.
[sp,values,rho] = spaps(x,y,tol) также возвращает фактическое значение ρ, используемого в качестве третьего выходного аргумента.
[...] = spaps(x,y,tol,arg1,arg2,...) позволяет вам задать вектор веса w и/или целочисленный m, путем предоставления их как argi. Для этого w должен быть неотрицательным вектором, одного размера как x; m должен быть 1 (для кусочного сплайна линейного сглаживания), или 2 (для кубического сплайна сглаживания по умолчанию), или 3 (для quintic, сглаживающего сплайн).
Если получившийся сплайн сглаживания, SP, должен быть оценен вне его основного интервала, он должен быть заменен fnxtr(sp,m), чтобы гарантировать, что его m-th производная является нулем вне того интервала.
[...] = spaps({x1,...,xr},y,tol,...) возвращает B-форму r - сплайн сглаживания продукта тензора варьируемой величины, который является примерно в заданном допуске к данным данным с координатной сеткой. (Для данных, имеющий разброс используйте tpaps.) Теперь y, как ожидают, предоставит соответствующие значения с координатной сеткой с size(y), равным [length(x1),...,length(xr)] в случае, если функция со скалярным знаком, и равна [d,length(x1),...,length(xr)] в случае, если функцией является d - оцененный. Далее, tol должен быть массивом ячеек с записями r с tol{i} допуск, используемый во время i-th шаг, когда одномерное (но с векторным знаком) сглаживающий сплайн в i-th переменная создается. Дополнительным входом для m должен быть r - вектор (с записями от набора {1,2,3}), и дополнительный вход для w должен быть массивом ячеек длины r с w{i} любой пустой (чтобы указать, что выбор по умолчанию требуется), или иначе положительный вектор той же длины как xi.
Операторы
w = ones(size(x)); w([1 end]) = 100; sp = spaps(x,y, 1.e-2, w, 3);
дайте quintic, сглаживающий приближение сплайна к определенным данным, которые близко к интерполируют первую и последнюю данную величину, будучи приблизительно в 1.e-2 остальных.
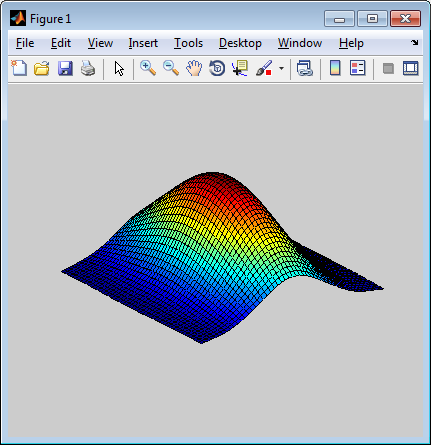
x = -2:.2:2; y=-1:.25:1; [xx,yy] = ndgrid(x,y); rng(39);
z = exp(-(xx.^2+yy.^2)) + (rand(size(xx))-.5)/30;
sp = spaps({x,y},z,8/(60^2)); fnplt(sp), axis off
производит фигуру ниже, показывая сглаженную аппроксимирующую функцию шумным данным из сглаженной двумерной функции. Отметьте использование ndgrid здесь; использование meshgrid привело бы к ошибке.
Подход Рейнша [1] используется (включая его умный способ выбрать уравнение для оптимального параметра сглаживания таким способом, которым хорошее исходное предположение доступно, и метод Ньютона, как гарантируют, будет сходиться и будет сходиться быстро).
[1] К. Рейнш. "Сглаживание функциями сплайна". Numer. Математика. 10 (1967), 177–183.