Экспериментируйте с некоторыми методами приближения сплайна
splinetool
splinetool(x,y)
splinetool графический интерфейс пользователя (GUI), исходное меню которого предоставляет вам различный выбор для данных включая опцию импортирования некоторых данных из рабочей области.
splinetool(x,y) поднимает графический интерфейс пользователя с заданными данными x и y, которые являются векторами той же длины.
Цель этого примера состоит в том, чтобы исследовать различные граничные условия, доступные с интерполяцией кубическим сплайном:
Введите splinetool в командной строке.
Выберите импортируют ваши собственные данные с начального экрана и принимают функцию по умолчанию. Необходимо видеть следующее отображение.
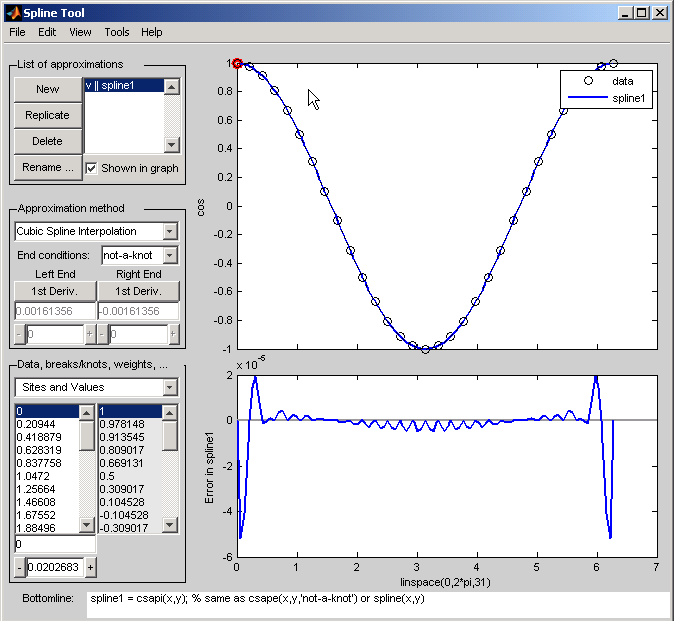
Показанное приближение по умолчанию является кубическим сплайном interpolant с граничным условием не-узла.
Векторным x сайтов данных является linspace(0,2*pi,31), и значениями является cos(x). Это отличается от простого обеспечения векторного y значений, в которых косинусная функция явным образом зарегистрирована как базовая функция. Поэтому ошибка, показанная в графике, является ошибкой в сплайне как приближение к косинусу, а не как приближение к данным значениям. Заметьте получившуюся относительно большую ошибку, о 5e-5, около конечных точек.
Для сравнения выполните эти шаги:
Нажмите на New в Списке приближений.
В методе Приближения выберите завершенный из списка Граничных условий.
Поскольку первая производная косинусной функции является синусом, настройте значения первой производной к их известным значениям нуля и в левом конце и в правильном конце.
Эта процедура приводит к отображению, показанному ниже (после того, как мышь будет использоваться, чтобы переместить Легенду далее вниз). Обратите внимание на то, что правильный наклон конца является нулем только до округления. Концевая строка говорит вам, что функция тулбокса csape использовалась, чтобы создать сплайн.
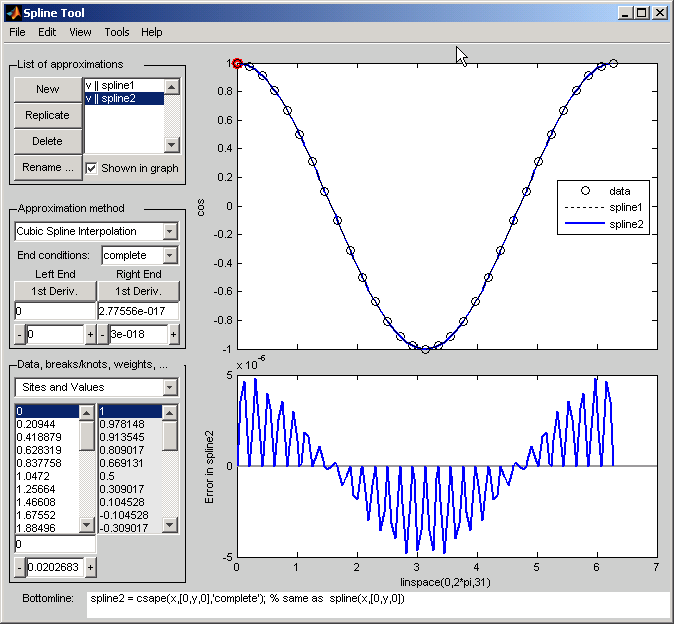
Будьте впечатлены улучшением ошибки, которая является только о 5e-6.
Для дальнейшего сравнения выполните эти шаги:
Нажмите на New в Списке приближений.
В методе Приближения выберите естественный из списка Граничных условий.
Отметьте ухудшение приближения около концов, ошибки приблизительно 2e-3, который намного хуже, чем с граничными условиями не-узла.
Для итогового сравнения выполните эти шаги:
Нажмите на New в Списке приближений.
Поскольку мы знаем, что косинусная функция является периодической в методе Приближения, выберите периодический из списка Граничных условий.
Отметьте поразительное улучшение приближения, назад к ошибке приблизительно 5e-6, особенно по сравнению с естественными граничными условиями.
Этот пример использует интерполяцию кубическим сплайном и приближение наименьших квадратов, чтобы определить оценку начального ускорения для автомобиля перетаскивания:
Введите splinetool в командной строке или если графический интерфейс пользователя уже запускается, нажмите на File> Restart.
Выберите Richard Tapia's перетаскивают мчащиеся данные. Эти данные показывают, что расстояние переместилось автомобилем перетаскивания как функция времени. Окно сообщения просит, чтобы вы оценили начальное ускорение путем обнуления начальной скорости. Нажмите на OK, или используйте Пространство или Войдите, чтобы удалить окно сообщения.
В методе Приближения выберите завершенный из списка Граничных условий.
Настройте начальную скорость путем изменения первой производной в левой конечной точке, чтобы обнулить.
Ищите значение начального ускорения, которое дано значением второй производной в левой конечной точке. Можно переключиться между первой производной и второй производной в этой конечной точке путем нажатия на левую кнопку конца. Значение второй производной должно быть вокруг 187 в выбранных модулях. Выберите View> Show 2-я Производная, чтобы видеть это графически.
Для сравнения нажмите на New, затем выберите Least-Squares Approximation в качестве метода Приближения. С этим методом вы больше не можете задавать граничные условия. Вместо этого можно отличаться порядок метода. Проверьте, что начальное ускорение близко к значению кубичной интерполяции.
Результаты этой процедуры показывают ниже.
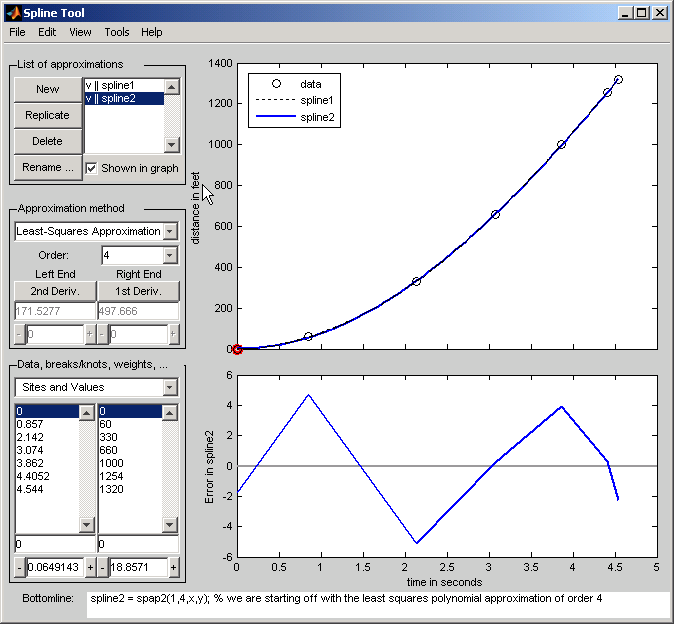
Этот пример поощряет вас помещать пять внутренних узлов таким способом, которым приближение наименьших квадратов к этим данным кубическими сплайнами имеет абсолютную погрешность, не больше, чем .04 везде:
Введите splinetool в командной строке или если графический интерфейс пользователя уже запускается, нажмите на File> Restart.
Выберите данные о тепле Titanium.
Выберите Least-Squares Approximation как метод Приближения.
Заметьте, как плохо это аппроксимирует данные, поскольку нет никаких внутренних узлов. Чтобы просмотреть текущие узлы и добавить новые узлы, выберите узлы из Данных, пропусков/узлы, весов. Узлы теперь перечислены в узлах, и также отображены в графике данных как вертикальные строки. Заметьте, что существует только два узла конца, каждый с кратностью 4.
Щелкните правой кнопкой по графику данных и выберите Add Knot. Это поднимает крест нитей для вас, чтобы переместиться с мышью. Его точное горизонтальное местоположение показывают в поле редактирования ниже списка узлов. Клик мыши помещает новый узел в текущем местоположении креста нитей. Одна возможная стратегия состоит в том, чтобы поместить дополнительный узел в месте максимальной абсолютной погрешности, как показано во вспомогательном графике ниже графика данных.
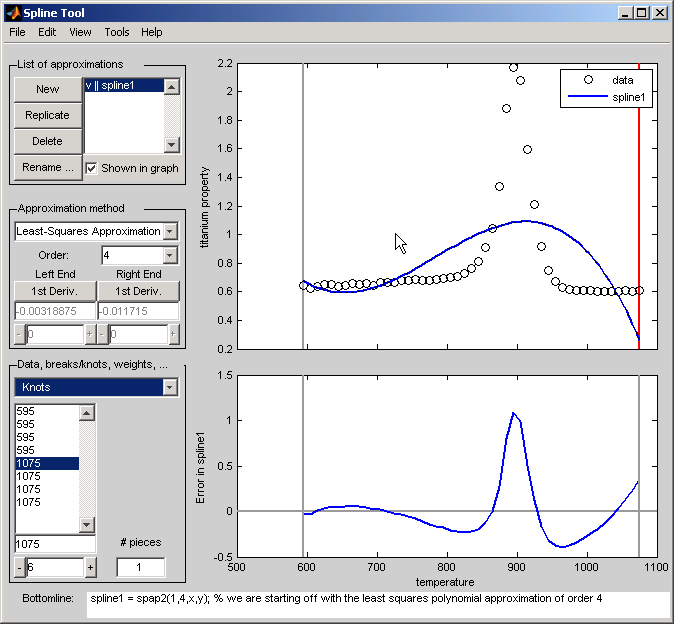
Если вы щелкнете правой кнопкой и выберете Replicate Knot, вы увеличите кратность текущего узла, который показывает его повторное вхождение в Узлах. Если вам не нравится конкретный узел, можно удалить его. Чтобы удалить определенный узел, необходимо сначала выбрать его или в списке узлов или в графике данных, и затем щелкнуть правой кнопкой по графику и выбрать Delete Knot.
Вы могли также попросить приближение с помощью шести полиномиальных частей, который соответствует пяти внутренним узлам. Для этого введите 6 как # части в Данных, пропусках/узлы, весах.
После того, как у вас будет пять внутренних узлов, попытайтесь совершить ошибку, еще меньшую путем перемещения узлов. Для этого выберите узел, который вы хотите переместить путем нажатия на его вертикальную строку в графике, затем использовать интерфейсное управление ниже Узлов в Данных, пропусках/узлы, весах и наблюдать, как ошибка изменяется с перемещением узла. Можно также использовать поле редактирования, чтобы перезаписать текущее местоположение узла. Вы могли также попробовать, настраивают, который перераспределяет текущую последовательность узла.
Использование Реплицирует в Список приближений, чтобы сохранить любое хорошее распределение узла для дальнейшего использования. Переименуйте реплицированное приближение к использованию lstsqr, Переименовывают. Чтобы возвратиться к исходному приближению, нажмите на его имя в Списке приближений.
Этот пример экспериментирует со сглаживанием сплайнов:
Введите splinetool в командной строке или, если графический интерфейс пользователя уже запускается, нажмите на File> Restart.
Выберите данные о тепле Titanium.
В методе Приближения выберите Smoothing Spline.
Отличайтесь Параметр между 0 и 1, который изменяет приближение от наименьших квадратов прямолинейное приближение к “естественному” кубическому сплайну interpolant.
Отличайтесь Допуск между 0 и некоторое большое значение, даже inf. Приближение изменяется от самого лучшего, “естественный” кубический сплайн interpolant, к наименьшим квадратам прямолинейное приближение.
Когда вы увеличиваете Значение параметров или уменьшаете значение Допуска, ошибочные уменьшения. Однако меньшая ошибка соответствует большему количеству шероховатости, как измерено размером второй производной. Чтобы видеть это, выберите View> Show 2-я Производная и отличайтесь значения Параметра и Допуска еще раз.
Этот шаг изменяет веса в ошибочной мере, чтобы обеспечить приближение, чтобы пройти через конкретную точку данных.
Установите Допуск на 0.2. Заметьте, что приближение не проходит через самую высокую точку данных. Чтобы видеть большую ошибку на этом сайте, выберите View> Error.
Чтобы обеспечить сплайн сглаживания, чтобы пройти эту точку, выберите Error Weights from Data, пропуски/узлы, веса.
Нажмите на самую высокую точку данных в графике и заметьте его сайт, который обозначается в Сайтах и Значениях.
Используйте поле редактирования ниже списка весов, чтобы изменить текущий вес на 1000. Заметьте, насколько ближе сплайн сглаживания теперь приходит к той самой высокой точке данных и уменьшению по ошибке на том сайте. Включите сетку, Инструментами> Сетка, чтобы определить местоположение ошибки на том сайте с большей готовностью.
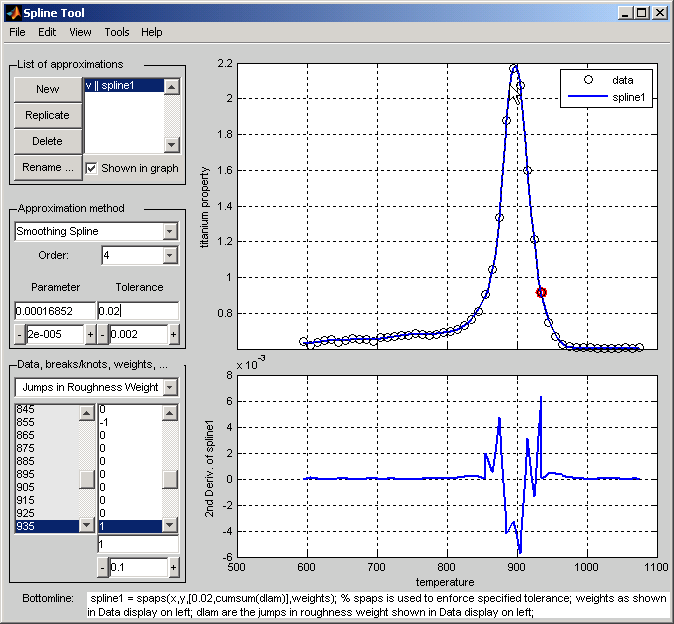
Этот шаг изменяет веса в мере по шероховатости, чтобы разрешить более точное, но менее сглаженное приближение в пиковой области при настаивании на более сглаженном, следовательно менее точном, приближение далеко от пиковой области.
Выберите Jumps in Roughness Weight from Data, пропуски/узлы, веса.
Выберите View> Show 2-я Производная
Выберите любую точку данных слева от пика в данных.
Установите скачок на выбранном сайте к -1 путем изменения его значения в поле редактирования ниже его. Поскольку вес шероховатости для самого первого интервала сайта равняется 1, вы только что установили вес шероховатости справа от подсвеченного сайта к 0. Соответственно, вторая производная стала относительно маленькой слева от того сайта.
Выберите любую точку данных справа от пика в данных.
Установите скачок через выбранный сайт к 1. Поскольку вес шероховатости только слева от подсвеченного сайта 0, вы только что установили вес шероховатости справа от подсвеченного сайта к 1. Соответственно, вторая производная стала относительно маленькой справа от того сайта. Общий эффект является очень сглаженным, но не очень точной подгонкой далеко от пика, в то время как в пиковой области, подгонка сплайна намного лучше, но вторая производная намного больше, как показан во вспомогательном графике ниже.
На сайтах, где во второй производной существует скачок в весе шероховатости, существует соответствующий скачок. Если вы увеличиваете Значение параметров, ошибку через пиковые уменьшения области, но вторая производная остается довольно большой, в то время как противоположное сохраняется далеко от пиковой области.
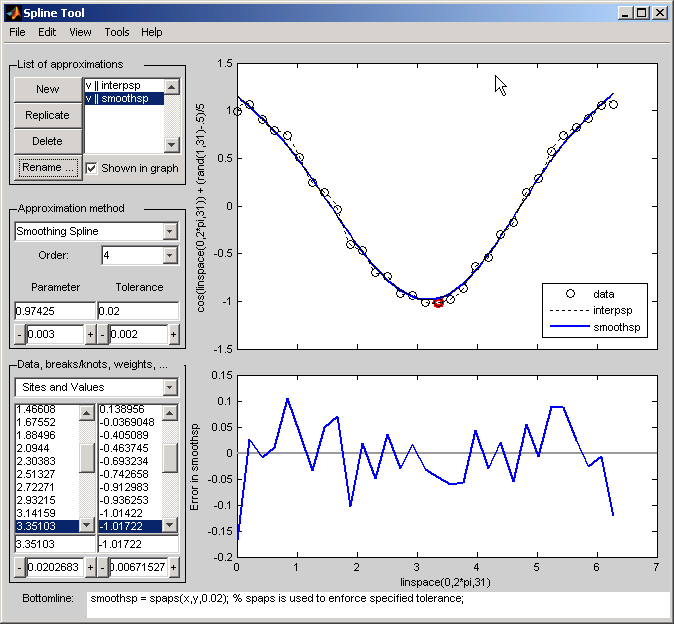
Инструмент Сплайна показывают в следующей фигуре, сравнивающей интерполяцию кубическим сплайном со сплайном сглаживания на выборочных данных, созданных путем добавления шума в косинусную функцию.
Методы приближения и опции, поддержанные графический интерфейсом пользователя, показывают ниже.
Метод приближения | Опция |
|---|---|
Кубический сплайн интерполяции | Настройте тип и значения граничных условий. |
Сглаживание сплайна | Выберите между кубическим (порядок 4) и quintic (порядок 6) сплайны. Настройте значение параметра сглаживания и/или допуска. Настройте веса в мерах по шероховатости и ошибке. |
Приближение наименьших квадратов | Отличайтесь порядок от 1 до 14. Порядок по умолчанию равняется 4, который дает кубические сплайны приближения. Измените количество полиномиальных частей. Добавьте и переместите узлы, чтобы улучшить подгонку. Настройте веса в ошибочной мере. |
Интерполяция сплайна | Отличайтесь порядок от 2 до 14. Порядок по умолчанию равняется 4, который дает кубический сплайн interpolants. Если предоставленные узлы по умолчанию не являются удовлетворительными, можно переместить их, чтобы отличаться подгонка. |
Можно сгенерировать и сравнить несколько приближений с теми же данными. Одно из приближений всегда отмечается как “текущее” использование более толстой ширины линии. Следующие отображения доступны:
График данных. Это показывает:
Данные
Приближения, выбранные для отображения в Списке приближений
Текущая последовательность узла или текущая последовательность пропуска
Вспомогательный график (если просматривается) для текущего приближения. Можно вызвать этот график путем выбора любого из элементов в меню View. Это показывает одно из следующего:
Первая производная
Вторая производная
Ошибка
По умолчанию ошибка является различием между значениями определенных данных и значением приближения на сайтах данных. В частности, ошибка является нулем (до округления), когда приближение является interpolant. Однако, если вы обеспечиваете значения данных путем определения функции, затем отображенная ошибка является различием между этой функцией и текущим приближением. Это также происходит, если вы изменяете y-метку графика данных к имени функции.
Можно аннотировать и распечатать графики с Файлом> Печать к меню Figure.
Можно экспортировать данные и приближения к рабочей области для дальнейшего использования или анализа с меню File> Export Data и File> Export Spline, соответственно.
Можно создать с меню File> Generate Code, файл функции, который можно использовать, чтобы сгенерировать, от исходных данных, любые графики, в настоящее время показанные. Этот файл также предоставляет, вы с записанной записью команд раньше генерировали текущий график (графики).
Можно сохранить с кнопкой Replicate, текущее приближение, прежде чем вы будете экспериментировать далее. Если в более позднее время вы нажимаете на приближение, таким образом сохраненное, splinetool восстанавливает все к способу, которым это было, включая данные, используемые в конструкции сохраненного приближения. Это верно, даже если начиная с сохранения этого приближения вы отредактировали данные при работе над другими приближениями.
Можно добавить, удалить или переместить данные, узлы и пропуски путем щелчка правой кнопкой по графику или выбора соответствующего элемента в меню Edit.
Можно переключить сетку или легенду в графике (графиках) с меню Tools.