Самоорганизующиеся карты функции (SOFM) учатся классифицировать входные векторы согласно тому, как они сгруппированы на входном пробеле. Они отличаются от конкурентоспособных слоев в тот, соседние нейроны в самоорганизующейся карте учатся распознавать соседние разделы входного пробела. Таким образом самоорганизующиеся карты изучают обоих распределение (также, как и конкурентоспособные слои) и топология входных векторов, на которых они обучены.
Нейроны в слое SOFM располагаются первоначально в физических положениях согласно функции топологии. Функциональный gridtop, hextop или randtop могут расположить нейроны в сетке, шестиугольной, или случайной топологии. Расстояния между нейронами вычисляются от их положений с функцией расстояния. Существует четыре функции расстояния, dist, boxdist, linkdist и mandist. Соединитесь расстояние наиболее распространено. Они топология и функции расстояния описаны в Топологии (gridtop, hextop, randtop) и Функции Расстояния (dist, linkdist, mandist, boxdist).
Здесь самоорганизующаяся сеть карты функции идентифицирует нейрон победы i* использование той же процедуры, как используется конкурентоспособным слоем. Однако вместо того, чтобы обновить только нейрон победы, все нейроны в определенном окружении Ni* (d) нейрона победы обновляются, используя правило Kohonen. А именно, все такие нейроны i ∊ Ni* (d) настроены можно следующим образом:
или
Здесь Ni окружения* (d) содержит индексы для всех нейронов, которые лежат в радиусе d нейрона победы i*.
Таким образом, когда вектор p представлен, веса нейрона победы и его близких соседей перемещаются к p. Следовательно, после многих представлений, соседние нейроны изучили векторы, подобные друг другу.
Другая версия обучения SOFM, названного пакетным алгоритмом, представляет целый набор данных сети, прежде чем любые веса будут обновлены. Алгоритм затем определяет нейрон победы для каждого входного вектора. Каждый вектор веса затем перемещается в среднее положение всех входных векторов, для которых это - победитель, или для которого это находится в окружении победителя.
Чтобы проиллюстрировать концепцию окружений, рассмотрите фигуру ниже. Левая схема показывает двумерное окружение радиуса d = 1 вокруг нейрона 13. Правильная схема показывает окружение радиуса d = 2.
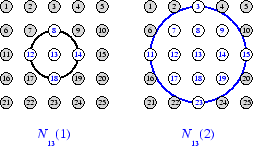
Эти окружения могли быть записаны как N 13 (1) = {8, 12, 13, 14, 18} и
N 13 (2) = {3, 7, 8, 9, 11, 12, 13, 14, 15, 17, 18, 19, 23}.
Нейроны в SOFM не должны быть расположены в двумерном шаблоне. Можно использовать одномерное расположение или три или больше размерности. Для одномерного SOFM нейрон имеет только двух соседей в радиусе 1 (или один сосед, если нейрон в конце строки). Можно также задать расстояние по-разному, например, при помощи прямоугольных и шестиугольных расположений нейронов и окружений. Производительность сети не чувствительна к точной форме окружений.
gridtop, hextop, randtop)Можно задать различную топологию для исходных местоположений нейрона с функциями gridtop, hextop и randtop.
Топология gridtop запускается с нейронов в прямоугольной сетке, подобной показанному в предыдущей фигуре. Например, предположите, что вы хотите массив 2х3 шести нейронов. Можно получить это с
pos = gridtop([2, 3])
pos =
0 1 0 1 0 1
0 0 1 1 2 2
Здесь нейрон 1 имеет положение (0,0), нейрон 2 имеет положение (1,0), и нейрон 3 имеет положение (0,1) и т.д.
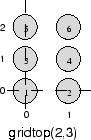
Обратите внимание на то, что попросили у вас gridtop с инвертированными размерами размерности, вы получите немного отличающееся расположение:
pos = gridtop([3, 2])
pos =
0 1 2 0 1 2
0 0 0 1 1 1
Можно создать 8 10 набор нейронов в топологии gridtop со следующим кодом:
pos = gridtop([8 10]); plotsom(pos)

Как показано нейроны в топологии gridtop действительно лежат на сетке.
Функция hextop создает подобный набор нейронов, но они находятся в шестиугольном шаблоне. 2 3 шаблон нейронов hextop сгенерирован можно следующим образом:
pos = hextop([2, 3])
pos =
0 1.0000 0.5000 1.5000 0 1.0000
0 0 0.8660 0.8660 1.7321 1.7321
Обратите внимание на то, что hextop является шаблоном по умолчанию для сетей SOM, сгенерированных с selforgmap.
Можно создать и построить 8 10 набор нейронов в топологии hextop со следующим кодом:
pos = hextop([8 10]); plotsom(pos)

Отметьте положения нейронов в шестиугольном расположении.
Наконец, функция randtop создает нейроны в N-мерном случайном шаблоне. Следующий код генерирует случайный шаблон нейронов.
pos = randtop([2, 3])
pos =
0 0.7620 0.6268 1.4218 0.0663 0.7862
0.0925 0 0.4984 0.6007 1.1222 1.4228
Можно создать и построить 8 10 набор нейронов в топологии randtop со следующим кодом:
pos = randtop([8 10]); plotsom(pos)

Для примеров смотрите справку для этих функций топологии.
dist, linkdist, mandist, boxdist)В этом тулбоксе существует четыре способа вычислить расстояния от конкретного нейрона до его соседей. Каждый метод расчета реализован со специальной функцией.
Функция dist вычисляет Евклидовы расстояния от домашнего нейрона до других нейронов. Предположим, что у вас есть три нейрона:
pos2 = [0 1 2; 0 1 2]
pos2 =
0 1 2
0 1 2
Вы находите расстояние от каждого нейрона до другого с
D2 = dist(pos2)
D2 =
0 1.4142 2.8284
1.4142 0 1.4142
2.8284 1.4142 0
Таким образом расстояние от нейрона 1 к себе 0, расстояние от нейрона 1 к нейрону 2 1.4142 и т.д.
График ниже показов домашний нейрон в двумерном слое (gridtop) нейронов. Домашний нейрон имеет окружения увеличивающегося диаметра, окружающего его. Окружение диаметра 1 включает домашний нейрон и его ближайших соседей. Окружение диаметра 2 включает диаметр 1 нейрон и их ближайшие соседи.
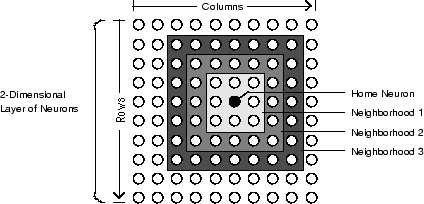
Что касается функции dist, все окружения для карты слоя S-нейрона представлены S-by-S матрицей расстояний. Особые расстояния, показанные выше (1 в мгновенном окружении, 2 в окружении 2, и т.д.), сгенерированы функциональным boxdist. Предположим, что у вас есть шесть нейронов в настройке gridtop.
pos = gridtop([2, 3])
pos =
0 1 0 1 0 1
0 0 1 1 2 2
d = boxdist(pos)
d =
0 1 1 1 2 2
1 0 1 1 2 2
1 1 0 1 1 1
1 1 1 0 1 1
2 2 1 1 0 1
2 2 1 1 1 0
Расстояние от нейрона 1 - 2, 3, и 4 равняется всего 1, поскольку они находятся в мгновенном окружении. Расстояние от нейрона 1 к и 5 и 6 равняется 2. Расстояние от и 3 и 4 ко всем другим нейронам равняется всего 1.
Расстояние ссылки от одного нейрона является только количеством ссылок или шагами, которые должны быть сделаны, чтобы добраться до нейрона на рассмотрении. Таким образом, если вы вычисляете расстояния от того же набора нейронов с linkdist, вы добираетесь
dlink =
0 1 1 2 2 3
1 0 2 1 3 2
1 2 0 1 1 2
2 1 1 0 2 1
2 3 1 2 0 1
3 2 2 1 1 0
Манхэттенское расстояние между двумя X и Y векторов вычисляется как
D = sum(abs(x-y))
Таким образом, если вы имеете
W1 = [1 2; 3 4; 5 6]
W1 =
1 2
3 4
5 6
и
P1 = [1;1]
P1 =
1
1
затем вы добираетесь для расстояний
Z1 = mandist(W1,P1)
Z1 =
1
5
9
Расстояния, вычисленные с mandist, действительно следуют за математическим выражением, данным выше.
Архитектуру для этого SOFM показывают ниже.
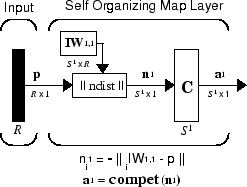
Эта архитектура похожа на архитектуру конкурентоспособной сети, ни кроме какого смещения используется здесь. Конкурентоспособная передаточная функция производит 1 для выходного элемента a1i соответствие i*, нейрон победы. Все другие выходные элементы в a1 0.
Теперь, однако, как описано выше, нейроны близко к нейрону победы обновляются наряду с нейроном победы. Можно выбрать из различной топологии нейронов. Точно так же можно принять решение из различных выражений расстояния вычислить нейроны, которые являются близко к нейрону победы.
selforgmap)Можно создать новую сеть SOM с функциональным selforgmap. Эта функция задает переменные, используемые в двух фазах изучения:
Эти значения используются для обучения и адаптации.
Рассмотрите следующий пример.
Предположим, что вы хотите создать сеть, имеющую входные векторы с двумя элементами, и что вы хотите иметь шесть нейронов в шестиугольном 2 3 сеть. Код, чтобы получить эту сеть:
net = selforgmap([2 3]);
Предположим, что векторы, чтобы обучаться на:
P = [.1 .3 1.2 1.1 1.8 1.7 .1 .3 1.2 1.1 1.8 1.7;...
0.2 0.1 0.3 0.1 0.3 0.2 1.8 1.8 1.9 1.9 1.7 1.8];Можно сконфигурировать сеть, чтобы ввести данные и построить все это с:
net = configure(net,P); plotsompos(net,P)

Зеленые пятна являются учебными векторами. Инициализация для selforgmap распространяет начальные веса через входной пробел. Обратите внимание на то, что они - первоначально некоторое расстояние от учебных векторов.
При симуляции сети отрицательные расстояния между вектором веса каждого нейрона и входным вектором вычисляются (negdist), чтобы получить взвешенные входные параметры. Взвешенные входные параметры являются также сетевыми входными параметрами (netsum). Сетевые входные параметры конкурируют (compet) так, чтобы только нейрон с самым положительным сетевым входом вывел 1.
learnsomb)Значение по умолчанию, учащееся в самоорганизующейся карте функции, происходит в пакетном режиме (trainbu). Функцией изучения веса для самоорганизующейся карты является learnsomb.
Во-первых, сеть идентифицирует нейрон победы для каждого входного вектора. Каждый вектор веса затем перемещается в среднее положение всех входных векторов, для которых это - победитель или для которого это находится в окружении победителя. Расстояние, которое задает размер окружения, изменено во время обучения через две фазы.
Эта фаза длится данное количество шагов. Расстояние окружения запускается на данном начальном расстоянии и уменьшается до настраивающегося расстояния окружения (1.0). Когда расстояние окружения уменьшается по этой фазе, нейроны сети обычно приказывают себя на входном пробеле с той же топологией, в которой им упорядочивают физически.
Эта фаза длится остальную часть обучения или адаптации. Размер окружения уменьшился ниже 1 поэтому, только нейрон победы учится для каждой выборки.
Теперь смотрите на некоторые определенные значения, обычно используемые в этих сетях.
Изучение происходит согласно параметру изучения learnsomb, показанному здесь с его значением по умолчанию.
Изучение параметра | Значение по умолчанию | Цель |
|---|---|---|
| 3 | Начальный размер окружения |
| 100 | Упорядоченное расположение шагов фазы |
Размер окружения NS изменен через две фазы: фаза упорядоченного расположения и настраивающаяся фаза.
Фаза упорядоченного расположения длится столько же шагов сколько LP.steps. Во время этой фазы алгоритм настраивает ND от начального размера окружения LP.init_neighborhood вниз к 1. Именно во время этой фазы веса нейрона приказывают себя на входном пробеле, сопоставимом со связанными положениями нейрона.
Во время настраивающейся фазы ND - меньше чем 1. Во время этой фазы веса, как ожидают, распространятся относительно равномерно по входному пробелу при сохранении их топологического порядка, найденного во время фазы упорядоченного расположения.
Таким образом векторы веса нейрона первоначально делают большие шаги все вместе к области входного пробела, где входные векторы происходят. Затем когда размер окружения уменьшается к 1, карта имеет тенденцию заказывать себя топологически по представленным входным векторам. Если размер окружения равняется 1, сеть должна быть довольно хорошо упорядочена. Обучение продолжается в порядке дать время нейронов, чтобы распространиться равномерно через входные векторы.
Как с конкурентоспособными слоями, нейроны самоорганизующейся карты прикажут себя приблизительно с равными расстояниями между ними, если входные векторы появятся с даже вероятностью в разделе входного пробела. Если входные векторы происходят с переменной частотой в течение входного пробела, слой карты функции имеет тенденцию выделять нейроны области в пропорции к частоте входных векторов там.
Таким образом покажите карты, при обучении категоризировать их вход, также изучать и топологию и распределение их входа.
Можно обучить сеть в течение 1 000 эпох с
net.trainParam.epochs = 1000; net = train(net,P); plotsompos(net,P)

Вы видите, что нейроны начали перемещаться к различным учебным группам. Дополнительное обучение требуется, чтобы получать нейроны ближе различным группам.
Как отмечено ранее, самоорганизующиеся карты отличаются от обычного конкурентоспособного изучения, с точки зрения которого нейроны обновили свои веса. Вместо того, чтобы обновить только победителя, карты функции обновляют веса победителя и ее соседей. Результат состоит в том, что соседние нейроны имеют тенденцию иметь подобные векторы веса и быть быстро реагирующими к подобным входным векторам.
Два примера описаны кратко ниже. Вы также можете попробовать подобные примеры demosm1 и demosm2.
Рассмотрите 100 двухэлементных модульных распространений входных векторов равномерно между 0 ° и 90 °.
angles = 0:0.5*pi/99:0.5*pi;
Вот график данных.
P = [sin(angles); cos(angles)];
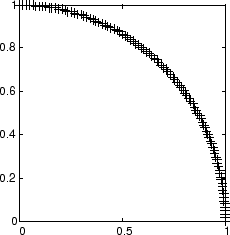
Самоорганизующаяся карта задана как одномерный слой 10 нейронов. Эта карта должна быть обучена на этих входных векторах, показанных выше. Первоначально эти нейроны находятся в центре фигуры.
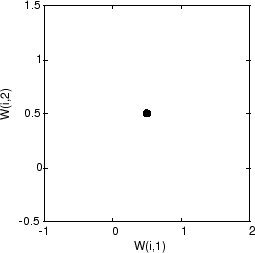
Конечно, потому что все векторы веса запускаются посреди пробела входного вектора, все, что вы видите, теперь один круг.
Когда обучение запускается, векторы веса двигаются вместе к входным векторам. Они также становятся упорядоченными, когда размер окружения уменьшается. Наконец слой настраивает свои веса так, чтобы каждый нейрон строго ответил на область входного места, занятого входными векторами. Размещение соседних векторов веса нейрона также отражает топологию входных векторов.
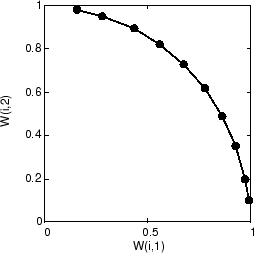
Обратите внимание на то, что самоорганизующиеся карты обучены с входными векторами в произвольном порядке, таким образом, начиная с тех же начальных векторов не гарантирует идентичные учебные результаты.
Этот пример показывает, как может быть обучена двумерная самоорганизующаяся карта.
Сначала некоторые случайные входные данные создаются со следующим кодом:
P = rands(2,1000);
Вот график этих 1 000 входных векторов.
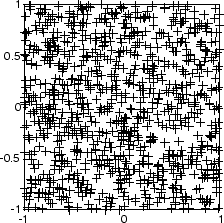
5 6 двумерная карта 30 нейронов используется, чтобы классифицировать эти входные векторы. Двумерная карта является пятью нейронами шестью нейронами с расстояниями, вычисленными согласно манхэттенской функции окружения расстояния mandist.
Карта затем обучена 5 000 циклов представления с отображениями каждые 20 циклов.
Вот то, на что самоорганизующаяся карта похожа после 40 циклов.
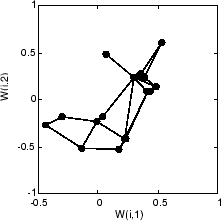
Векторы веса, показанные с кругами, почти случайным образом помещаются. Однако даже только после 40 циклов представления, соседние нейроны, соединенные строками, имеют векторы веса близко друг к другу.
Вот карта после 120 циклов.
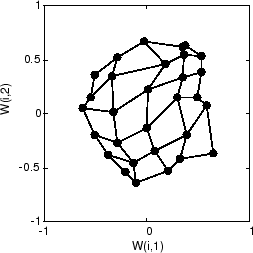
После 120 циклов карта начала организовывать себя согласно топологии входного пробела, который ограничивает входные векторы.
Следующий график, после 500 циклов, показывает карту, более равномерно распределенную через входной пробел.
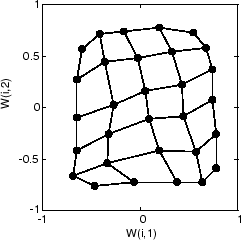
Наконец, после 5 000 циклов, карта скорее равномерно распространена через входной пробел. Кроме того, нейроны очень равномерно расположены с интервалами, отразив ровное распределение входных векторов в этой проблеме.
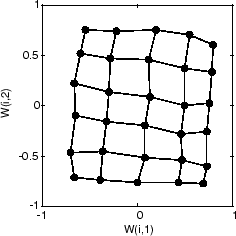
Таким образом двумерная самоорганизующаяся карта изучила топологию пробела своих входных параметров.
Важно отметить, что, в то время как самоорганизующаяся карта не занимает много времени организовывать себя так, чтобы соседние нейроны распознали подобные входные параметры, может требоваться много времени для карты, чтобы наконец расположить себя согласно распределению входных векторов.
Пакетный учебный алгоритм обычно намного быстрее, чем инкрементный алгоритм, и это - алгоритм по умолчанию для обучения SOFM. Можно экспериментировать с этим алгоритмом на простом наборе данных со следующими командами:
x = simplecluster_dataset net = selforgmap([6 6]); net = train(net,x);
Эта последовательность команды создает и обучает 6 6 двумерную карту 36 нейронов. Во время обучения появляется следующая фигура.
Существует несколько полезной визуализации, к которой можно получить доступ из этого окна. Если вы нажимаете SOM Weight Positions, следующая фигура появляется, который показывает местоположения точек данных и векторов веса. Как фигура указывает, только после 200 итераций пакетного алгоритма карта хорошо распределяется через входной пробел.
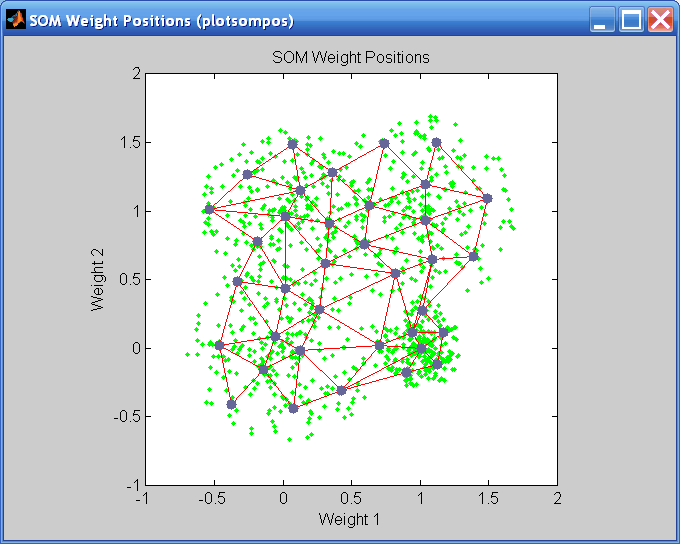
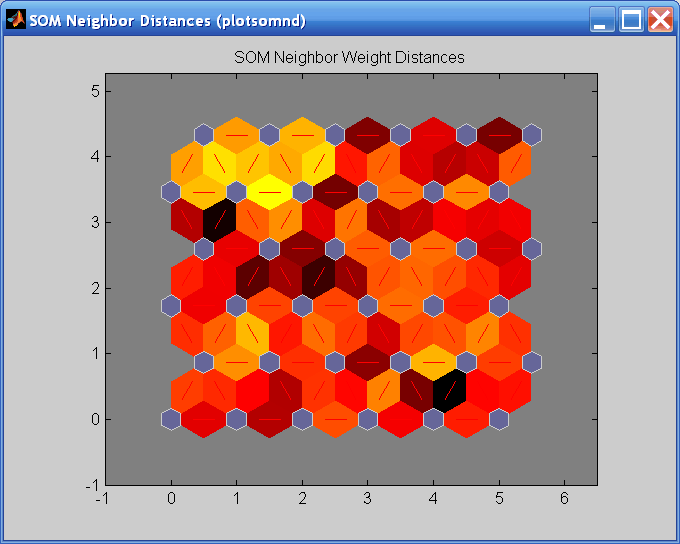
Когда входной пробел является высоко размерным, вы не можете визуализировать все веса одновременно. В этом случае нажмите SOM Neighbor Distances. Следующая фигура появляется, который указывает на расстояния между соседними нейронами.
Эта фигура использует следующую расцветку:
Синие шестиугольники представляют нейроны.
Нейроны граничения подключения красных линий.
Цвета в областях, содержащих красные линии, указывают на расстояния между нейронами.
Более темные цвета представляют большие расстояния.
Более легкие цвета представляют меньшие расстояния.
Группа легких сегментов появляется в верхней левой области, ограниченной некоторыми более темными сегментами. Эта группировка указывает, что сеть кластеризировала данные в две группы. Эти две группы видны в предыдущей фигуре положения веса. Нижняя правая область той фигуры содержит небольшую группу плотно кластеризованных точек данных. Соответствующие веса ближе вместе в этой области, которая обозначается, легче раскрашивает соседнюю фигуру расстояния. Где веса в этой небольшой области соединяются с более крупной областью, расстояния больше, как обозначено более темной полосой в соседней фигуре расстояния. Сегменты в нижней правой области соседней фигуры расстояния являются более темными, чем те в верхнем левом углу. Это цветовое различие указывает, что точки данных в этой области более далеки независимо. Это расстояние подтверждено в фигуре положений веса.
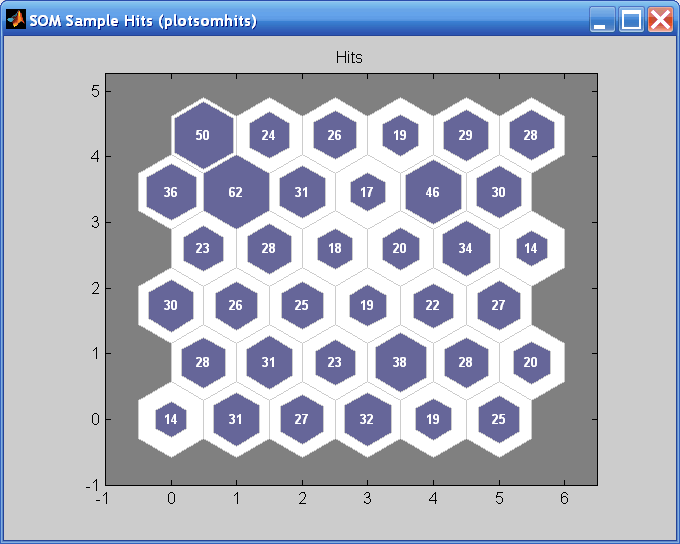
Другая полезная фигура может сказать вам, сколько точек данных сопоставлено с каждым нейроном. Нажмите SOM Sample Hits, чтобы видеть следующую фигуру. Лучше, если данные справедливо равномерно распределяются через нейроны. В этом примере данные сконцентрированы немного больше в верхних левых нейронах, но в целом распределение довольно ровно.
Можно также визуализировать сами веса с помощью плоской фигуры веса. Нажмите SOM Weight Planes в учебном окне, чтобы получить следующую фигуру. Существует плоскость веса для каждого элемента входного вектора (два, в этом случае). Они - визуализация весов, которые соединяют каждый вход с каждым из нейронов. (Более легкие и более темные цвета представляют большие и меньшие веса, соответственно.), Если шаблоны связи двух входных параметров очень похожи, можно принять, что входные параметры высоко коррелировались. В этом случае введите 1, имеет связи, которые очень отличаются, чем те из входа 2.
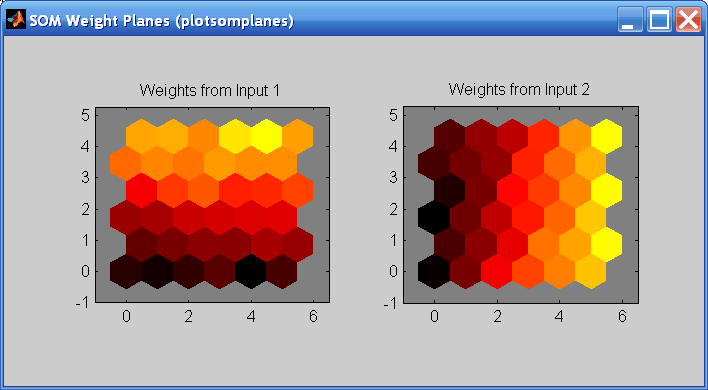
Можно также произвести все предыдущие фигуры из командной строки. Попробуйте эти команды графического вывода: plotsomhits, plotsomnc, plotsomnd, plotsomplanes, plotsompos и plotsomtop.