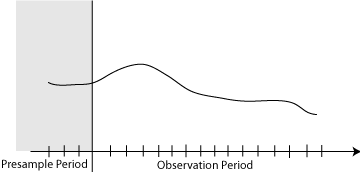
Presample data прибывает из моментов времени перед началом периода наблюдения. В Econometrics Toolbox™ можно задать собственные преддемонстрационные данные или использование сгенерированные преддемонстрационные данные.
В моделях регрессии с ошибками ARIMA распределение текущих инноваций (εt) является условным выражением на historic information (Ht). Историческая информация может включать прошлые безусловные воздействия или прошлые инновации, т.е. Ht = {u t – 1, ε t – 1, u t – 2, ε t – 2..., u 0, ε 0, u –1, ε –1...}. Однако программное обеспечение не включает прошлые ответы (yt), ни прошлые предикторы (Xt) в Ht. Например, в модели регрессии с ARIMA (2,1,1) ошибки, можно записать ошибочную модель несколькими способами:
Последнее уравнение подразумевает что:
Первые инновации в ряду (ε 1) зависят от истории H 1 = {u –2, u –1, u 0, ε 0}. H 1 не заметен, ни выводим из модели регрессии.
Вторые инновации в ряду (ε 2) зависят от истории H 2 = {u –1, u 0, u 1, ε 1}. Программное обеспечение может вывести u 1 и ε 1, но не другие.
Третьи инновации в ряду (ε 3) зависят от истории H 3 = {u 0, u 1, u 2, ε 2}. Программное обеспечение может вывести u 1, u 2, и ε 1, но не u 0.
Остальная часть инноваций зависит от выводимых безусловных воздействий и инноваций.
Поэтому программное обеспечение требует, чтобы три преддемонстрационных безусловных воздействия инициализировали авторегрессивный фрагмент и преддемонстрационные инновации, чтобы инициализировать фрагмент скользящего среднего значения.
Степени составных полиномов авторегрессивного и скользящего среднего значения определяют количество прошлых безусловных воздействий и инноваций, от которых зависит εt. Составной авторегрессивный полином включает сезонные и несезонные авторегрессивные, и сезонные и несезонные полиномы интегрирования. Составной полином скользящего среднего значения включает сезонные и несезонные полиномы скользящего среднего значения. В примере степенью составного авторегрессивного полинома является P = 3, и степенью полинома скользящего среднего значения является Q = 1. Поэтому программное обеспечение требует трех преддемонстрационных безусловных воздействий и преддемонстрационных инноваций.
Если у вас нет преддемонстрационных значений (или не предоставляйте их), то, по умолчанию, обратные броски программного обеспечения для необходимых преддемонстрационных безусловных воздействий, и устанавливает необходимые преддемонстрационные инновации на 0.
Другая опция, чтобы получить преддемонстрационные безусловные воздействия должна разделить набор данных в преддемонстрационный фрагмент и фрагмент оценки:
Разделите данные, таким образом, что преддемонстрационный фрагмент содержит, по крайней мере, наблюдения max(P,Q). Программное обеспечение использует новые наблюдения max(P,Q) и игнорирует остальных.
Для преддемонстрационного фрагмента регрессируйте yt на Xt.
Выведите невязки из модели регрессии. Это преддемонстрационные безусловные воздействия.
Передайте преддемонстрационные безусловные воздействия (U0) и фрагмент оценки данных в estimate.
Эта опция приводит к потере объема выборки. Обратите внимание на то, что при сравнении многоуровневых моделей с помощью основанных на вероятности мер подгонки (таких как тесты отношения правдоподобия или информационные критерии), затем данные должны иметь те же фрагменты оценки, и преддемонстрационные фрагменты должны иметь равный размер.
Если вы планируете определение преддемонстрационных значений, то необходимо задать, по крайней мере, номер, необходимый, чтобы инициализировать ряд.
Можно задать и преддемонстрационные безусловные воздействия и инновации, один или другой или ни один.