abs2active

Примеры

Настройте ограничения для оптимизации портфеля для портфеля w0 с ограничениями в форме A*w <= b, где w является абсолютными весами портфеля. (Абсолютные веса не зависят от портфеля отслеживания.) Используют abs2active, чтобы преобразовать ограничения с точки зрения абсолютных весов в ограничения с точки зрения активных весов портфеля, заданных относительно портфеля отслеживания w0. Примите три актива со следующим средним значением, и ковариация актива возвращается:

m = [ 0.14; 0.10; 0.05 ];
C = [ 0.29^2 0.4*0.29*0.17 0.1*0.29*0.08; 0.4*0.29*0.17 0.17^2 0.3*0.17*0.08;...
0.1*0.29*0.08 0.3*0.17*0.08 0.08^2 ];

Абсолютные ограничения портфеля являются типичными единицами (сумма весов к 1 и падение от 0 до 1), создают A и матрицы b с помощью portcons:

AbsCons = portcons('PortValue',1,3,'AssetLims', [0; 0; 0], [1; 1; 1;]);

Используйте объект Portfolio определить границу эффективности:

p = Portfolio('AssetMean', m, 'AssetCovar', C);
p = p.setInequality(AbsCons(:,1:end-1), AbsCons(:,end));
p.plotFrontier;

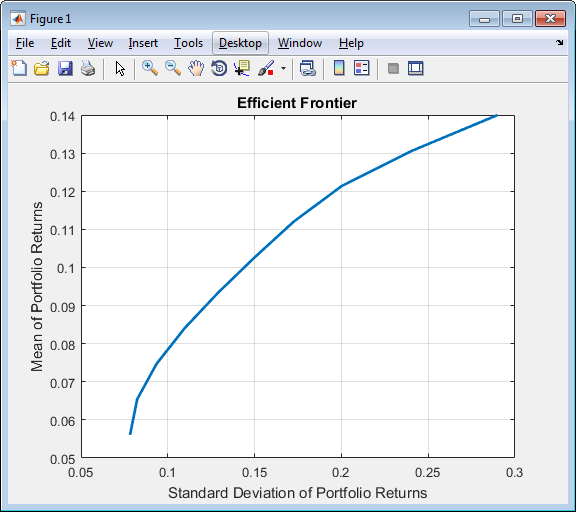
Портфель отслеживания w0:

w0 = [ 0.1; 0.55; 0.35 ];

Используйте abs2active, чтобы вычислить ограничения для активных весов портфеля:

ActCons = abs2active(AbsCons, w0)

Это возвращается:

ActCons =

    1.0000    1.0000    1.0000         0
   -1.0000   -1.0000   -1.0000         0
    1.0000         0         0    0.9000
         0    1.0000         0    0.4500
         0         0    1.0000    0.6500
   -1.0000         0         0    0.1000
         0   -1.0000         0    0.5500
         0         0   -1.0000    0.3500

Используйте объект Portfolio p и его граница эффективности, чтобы продемонстрировать ожидаемые доходы и риск относительно портфеля отслеживания w0:

p = p.setInequality(ActCons(:,1:end-1), ActCons(:,end));
p.plotFrontier;

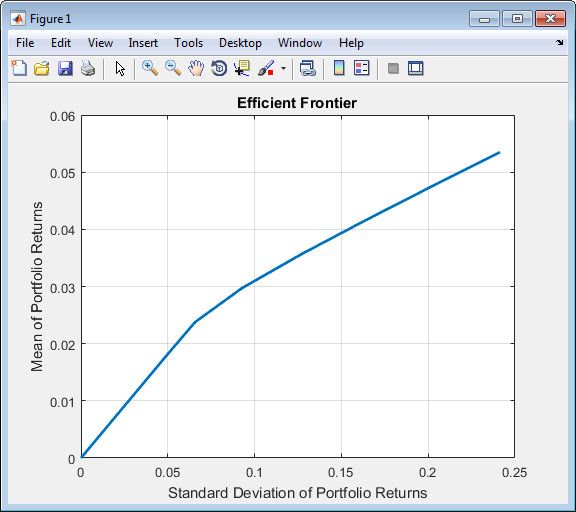
Отметьте, при использовании abs2active, чтобы вычислить “активные ограничения” для использования с объектом Portfolio, не использовать ограничения объекта Portfolio по умолчанию, потому что относительные веса могут быть положительными или отрицательными (функция setDefaultConstraints задает веса, чтобы быть неотрицательной).