Можно оценить нелинейные модели ARX после того, как вы выполните следующие задачи:
Подготовьте свои данные, как описано в Подготовка данных для Нелинейной Идентификации.
(Необязательно) модель Estimate заказывает и задерживает тот же способ, которым вы были бы для линейных моделей ARX. Смотрите Предварительный Шаг – Оценка Порядков Модели и Входных Задержек.
(Необязательно) Выберите средство оценки нелинейности в Доступных Средствах оценки Нелинейности для Нелинейных Моделей ARX.
(Необязательно) Оценка или построение линейная модель ARX для инициализации нелинейной модели ARX. Смотрите Инициализируют Нелинейную Оценку ARX Используя Линейную Модель.
nlarxИспользуйте nlarx, чтобы и создать и оценить нелинейную модель ARX. После каждой оценки подтвердите модель путем сравнения его с другими моделями и симуляции или предсказания образцового ответа.
Основная оценка
Запустите с самой простой оценки с помощью m = nlarx(data,[na nb nk]). Например:
load iddata1; % na = nb = 2 and nk = 1 m = nlarx(z1,[2 2 1])
m = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Standard regressors corresponding to the orders: na = 2, nb = 2, nk = 1 No custom regressor Nonlinear regressors: y1(t-1) y1(t-2) u1(t-1) u1(t-2) Nonlinearity: wavenet with 1 unit Sample time: 0.1 seconds Status: Estimated using NLARX on time domain data "z1". Fit to estimation data: 68.83% (prediction focus) FPE: 1.975, MSE: 1.885
Второй входной параметр [na nb nk] задает порядки модели и задержки. По умолчанию средство оценки нелинейности является сетью вейвлета (см. страницу с описанием wavenet), который берет все стандартные регрессоры в качестве входных параметров к ее линейным и нелинейным функциям. m является объектом idnlarx.
Для систем MIMO nb, nf и nk является ny-by-nu матрицы. Смотрите страницу с описанием nlarx для получения дополнительной информации об оценке MIMO.
Задайте различное средство оценки нелинейности (например, сигмоидальная сеть).
M = nlarx(z1,[2 2 1],'sigmoid');Создайте набор опции nlarxOptions и сконфигурируйте свойство Focus минимизировать ошибку симуляции.
opt = nlarxOptions('Focus','simulation'); M = nlarx(z1,[2 2 1],'sigmoid',opt);
Стандартные регрессоры
Измените порядок модели создать образцовую структуру с различными образцовыми регрессорами, которые являются задержанными переменными ввода и вывода, которые являются входными параметрами к средству оценки нелинейности.
Пользовательские регрессоры
Исследуйте включая пользовательские регрессоры в нелинейной структуре модели ARX. Пользовательские регрессоры в дополнение к стандартным образцовым регрессорам (см. Нелинейные Порядки Модели ARX и Задержку).
Используйте polyreg или customreg, чтобы создать пользовательские регрессоры с точки зрения образцовых переменных ввода - вывода. Можно задать пользовательские регрессоры с помощью свойства CustomRegressors класса idnlarx или addreg, чтобы добавить пользовательские регрессоры к существующей модели.
Например, сгенерируйте регрессоры как полиномиальные функции вводов и выводов:
load iddata1 m = nlarx(z1,[2 2 1],'sigmoidnet'); getreg(m) % displays all regressors
Regressors:
y1(t-1)
y1(t-2)
u1(t-1)
u1(t-2)
% Generate polynomial regressors up to order 2:
reg = polyreg(m)4x1 array of Custom Regressors with fields: Function, Arguments, Delays, Vectorized
Добавьте полиномиальные регрессоры к CustomRegressors.
m = addreg(m,reg); getreg(m)
Regressors:
y1(t-1)
y1(t-2)
u1(t-1)
u1(t-2)
y1(t-1).^2
y1(t-2).^2
u1(t-1).^2
u1(t-2).^2
m теперь включает полиномиальные регрессоры.
Можно также задать произвольные функции переменных ввода и вывода. Например:
load iddata1 m = nlarx(z1,[2 2 1],'sigmoidnet','CustomReg',{'y1(t-1)^2','y1(t-2)*u1(t-3)'}); getreg(m) % displays all regressors
Regressors:
y1(t-1)
y1(t-2)
u1(t-1)
u1(t-2)
y1(t-1)^2
y1(t-2)*u1(t-3)
Добавьте полиномиальные регрессоры к CustomRegressors.
m = addreg(m,reg);
getreg(m) % polynomial regressorsRegressors:
y1(t-1)
y1(t-2)
u1(t-1)
u1(t-2)
y1(t-1)^2
y1(t-2)*u1(t-3)
y1(t-1).^2
y1(t-2).^2
u1(t-1).^2
u1(t-2).^2
Управляйте пользовательскими регрессорами с помощью свойства CustomRegressors класса idnlarx. Например, чтобы получить указатель на функцию первого пользовательского регрессора в массиве:
CReg1 = m.CustomReg(1).Function;
Просмотрите выражение регрессора.
m.CustomReg(1).Display
ans = 'y1(t-1)^2'
Можно исключить все стандартные регрессоры и использовать только пользовательские регрессоры в образцовой структуре установкой na=nb=nk=0:
m = nlarx(z1,[0 0 0],'linear','CustomReg',{'y1(t-1)^2','y1(t-2)*u1(t-3)'});
В усовершенствованных приложениях можно задать усовершенствованные опции оценки для средств оценки нелинейности. Например, wavenet и классы treepartition обеспечивают свойство Options для установки таких опций оценки.
По умолчанию все образцовые регрессоры входят как входные параметры и в линейные и в нелинейные функциональные блоки средства оценки нелинейности. Чтобы уменьшать сложность модели и сохранить оценку хорошо подготовленной, используйте подмножество регрессоров как входные параметры к нелинейной функции нелинейного блока средства оценки. Например, задайте нелинейную модель ARX, чтобы быть линейными в мимо выходных параметров и нелинейными в прошлых входных параметрах.
m = nlarx(z1,[2 2 1]); % all standard regressors are % inputs to the nonlinear function getreg(m); % lists all standard regressors
Regressors:
y1(t-1)
y1(t-2)
u1(t-1)
u1(t-2)
m = nlarx(z1,[4 4 1],sigmoidnet,'nlreg',[5 6 7 8]);Этот пример использует getreg, чтобы определить индекс каждого регрессора из полного списка всех образцовых регрессоров. Только регрессор числа 5 - 8 является входными параметрами к нелинейной функции - getreg показывает, что эти регрессоры являются функциями входной переменной u1. nlreg является сокращением от свойства NonlinearRegressors класса idnlarx. Также включайте только входные регрессоры в нелинейное использование функционального блока:
m = nlarx(z1,[4 4 1],sigmoidnet,'nlreg','input');
Когда вы не будете уверены, который регрессоры включать как входные параметры к нелинейному функциональному блоку, задайте, чтобы искать во время оценки оптимальную комбинацию регрессора:
m = nlarx(z1,[4 4 1],sigmoidnet,'nlreg','search');
Этот поиск обычно занимает много времени. Можно отобразить поисковое использование прогресса:
opt = nlarxOptions('Display','on'); m = nlarx(z1,[4 4 1],sigmoidnet,'nlreg','search',opt);
После оценки используйте m.NonlinearRegressors, чтобы просмотреть, какие регрессоры были выбраны автоматическим поиском регрессора.
m.NonlinearRegressors
ans = 1×4
3 5 6 7
Задайте средство оценки нелинейности непосредственно в команде оценки как:
Вектор символов имени нелинейности, которое использует настройку нелинейности по умолчанию.
m = nlarx(z1, [2 2 1],'sigmoidnet');Объект Nonlinearity.
m = nlarx(z1,[2 2 1],wavenet('num',5));Эта оценка использует нелинейную модель ARX с нелинейностью вейвлета, которая имеет 5 модулей. Создать объект нелинейности прежде если это как вход к средству оценки нелинейности:
w = wavenet('num', 5); m = nlarx(z1,[2 2 1],w); % or w = wavenet; w.NumberOfUnits = 5; m = nlarx(z1,[2 2 1],w);
Для систем MIMO можно задать различную нелинейность для каждого вывода. Например, чтобы задать sigmoidnet для первого вывода и wavenet для второго вывода:
load iddata1 z1 load iddata2 z2 data = [z1, z2(1:300)]; M = nlarx(data,[[1 1;1 1] [2 1;1 1] [2 1;1 1]],[sigmoidnet wavenet]);
Если вы хотите ту же нелинейность для всех выходных каналов, задаете одну нелинейность.
M = nlarx(data,[[1 1;1 1] [2 1;1 1] [2 1;1 1]],sigmoidnet);
Следующая таблица обобщает значения, которые задают средства оценки нелинейности.
| Нелинейность | Значение (настройка нелинейности по умолчанию) | Класс |
|---|---|---|
| Сеть Wavelet (значение по умолчанию) | 'wavenet' или 'wave' | wavenet |
| Один слой сигмоидальная сеть | 'sigmoidnet' или 'sigm' | sigmoidnet |
| Древовидный раздел | 'treepartition' или 'tree' | treepartition |
| F линеен в x | 'linear' или [ ] | linear |
Дополнительная доступная нелинейность включает многослойные нейронные сети и пользовательские сети, которые вы создаете.
Задайте многослойное использование нейронной сети:
m = nlarx(data,[na nb nk],NNet)
где NNet является объектом нейронной сети, вы создаете использование программного обеспечения Deep Learning Toolbox™. Смотрите страницу с описанием neuralnet.
Задайте пользовательскую сеть путем определения функции под названием gaussunit.m, как описано на странице с описанием customnet. Задайте пользовательский сетевой объект CNetw и оцените модель:
CNetw = customnet(@gaussunit); m = nlarx(data,[na nb nk],CNetw)
Если ваша модель включает wavenet, sigmoidnet и средства оценки нелинейности customnet, можно исключить линейную функцию с помощью свойства LinearTerm средства оценки нелинейности. Средство оценки нелинейности становится F (x) =.
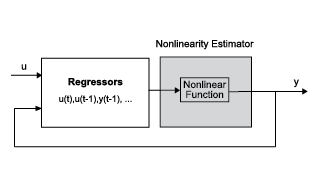
Например:
SNL = sigmoidnet('LinearTerm','off'); m = nlarx(z1,[2 2 1],SNL);
Вы не можете исключить линейную функцию от древовидного раздела и средств оценки нелинейности нейронной сети.
Сконфигурируйте нелинейную структуру ARX, чтобы включать только линейную функцию в средство оценки нелинейности путем установки нелинейности на linear. В этом случае, F (x) = взвешенная сумма образцовых регрессоров плюс смещение. Такие модели обеспечивают мост между чисто линейными моделями ARX и полностью гибкими нелинейными моделями.
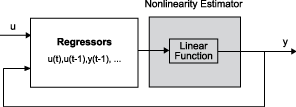
В самом простом случае модель только со стандартными регрессорами линейна (аффинно). Например, эта структура:
m = nlarx(z1,[2 2 1],'linear');подобно линейной модели ARX:
lin_m = arx(z1,[2 2 1]);
Однако нелинейная модель m ARX более гибка, чем линейная модель ARX lin_m, потому что это содержит срок смещения, d. Этот срок смещения обеспечивает дополнительную гибкость получения смещений сигнала, который не доступен в линейных моделях.
Популярная нелинейная настройка ARX во многих приложениях использует полиномиальные регрессоры для системной нелинейности модели. В таких случаях система считается линейной комбинацией продуктов (задержанных) переменных ввода и вывода. Используйте команду polyreg, чтобы легко сгенерировать комбинации продуктов регрессора и степеней.
Например, предположите, что вы знаете, что вывод y (t) системы линейная комбинация (y (t − 1)) 2 и y (t − 2) *u (t − 3). Чтобы смоделировать такую систему, используйте:
M = nlarx(z1,[0 0 0],'linear','CustomReg',{'y1(t-1)^2','y1(t-2)*u1(t-3)'});
M не имеет никаких стандартных регрессоров, и нелинейность в модели описана только пользовательскими регрессорами.
Если ваша образцовая структура включает нелинейность, которая поддерживает итеративный поиск (см., Задают Опции Оценки для Нелинейных Моделей ARX), можно использовать nlarx, чтобы совершенствовать параметры модели:
m1 = nlarx(z1,[2 2 1],'sigmoidnet'); m2 = nlarx(z1,m1); % can repeatedly run this command
Можно также использовать pem, чтобы совершенствовать исходную модель:
m2 = pem(z1,m1);
Проверяйте поисковый критерий завершения m.Report.Termination.WhyStop. Если WhyStop указывает, что оценка достигла максимального количества итераций, попытайтесь повторить оценку и возможно задать большее значение для опции оценки nlarxOptions.SearchOptions.MaxIterations:
opt = nlarxOptions; opt.SearchOptions.MaxIterations = 30; m2 = nlarx(z1,m1,opt); % runs 30 more iterations % starting from m1
Когда значением m.Report.Termination.WhyStop является Near (local) minimum, (norm( g) < tol или No improvement along the search direction with line search, подтвердите свою модель, чтобы видеть, соответствует ли эта модель соответственно данным. В противном случае решение может застрять в локальном минимуме поверхности функции стоимости. Попытайтесь настроить значение SearchOptions.Tolerance или опцию SearchMethod в nlarxOptions наборе опции, и повторите оценку.
Можно также попытаться тревожить параметры последней модели с помощью init (названный рандомизацией) и совершенствовав модель с помощью nlarx:
M1 = nlarx(z1, [2 2 1], 'sigm'); % original model M1p = init(M1); % randomly perturbs parameters about nominal values M2 = nlarx(z1, M1p); % estimates parameters of perturbed model
Можно отобразить прогресс итеративного поиска в Окне Команды MATLAB с помощью опции оценки nlarxOptions.Display:
opt = nlarxOptions('Display','on'); M2= nlarx(z1,M1p,opt);
Если вы не получаете удовлетворительную модель после многих испытаний с различными образцовыми структурами и настроек алгоритма, возможно, что данные плохи. Например, ваши данные могут пропускать важные переменные ввода или вывода и не достаточно отвечают на все рабочие вопросы системы.
Нелинейная система идентификации черного ящика обычно требует, чтобы больше данных, чем линейная образцовая идентификация получило достаточно информации о системе.
Этот пример показывает, как использовать nlarx, чтобы оценить нелинейную модель ARX для измеренных данных о вводе/выводе.
Подготовьте данные к оценке.
load twotankdata
z = iddata(y, u, 0.2);
ze = z(1:1000); zv = z(1001:3000);Оцените несколько моделей с помощью различных порядков модели, задержек и настроек нелинейности.
m1 = nlarx(ze,[2 2 1]); m2 = nlarx(ze,[2 2 3]); m3 = nlarx(ze,[2 2 3],wavenet('num',8)); m4 = nlarx(ze,[2 2 3],wavenet('num',8),... 'nlr', [1 2]);
Альтернативный способ выполнить оценку состоит в том, чтобы сконфигурировать образцовую структуру сначала, и затем оценить эту модель.
m5 = idnlarx([2 2 3],sigmoidnet('num',14),'nlr',[1 2]); m5 = nlarx(ze,m5);
Сравните получившиеся модели путем графического вывода образцовых выходных параметров с измеренным выводом.
compare(zv, m1,m2,m3,m4,m5)
