Оцените параметры нелинейной модели ARX
sys = nlarx(Data,Orders)sys = nlarx(Data,Orders,Nonlinearity)sys = nlarx(Data,Orders,Nonlinearity,Name,Value)sys = nlarx(Data,LinModel)sys = nlarx(Data,LinModel,Nonlinearity) sys = nlarx(Data,LinModel,Nonlinearity,Name,Value)sys = nlarx(Data,sys0)sys = nlarx(___,Options)sys = nlarx(Data,Orders,Nonlinearity)
sys = nlarx(Data,Orders,Nonlinearity,Name,Value)Name,Value. Эти атрибуты включают нелинейную и пользовательскую структуру регрессора и свойства данных модели idnlarx.
sys = nlarx(Data,LinModel,Nonlinearity)
sys = nlarx(Data,LinModel,Nonlinearity,Name,Value)idnlarx с помощью одного или нескольких аргументов пары Name,Value.
sys = nlarx(Data,sys0)sys0.
Используйте этот синтаксис для:
Обновите параметры ранее предполагаемой модели, чтобы улучшить подгонку к данным об оценке. В этом случае алгоритм оценки использует параметры sys0 как исходные предположения.
Оцените, что параметры модели ранее создали использование конструктора idnlarx. До оценки можно сконфигурировать образцовые свойства с помощью записи через точку.
Загрузите данные об оценке.
load twotankdata;Создайте объект iddata из данных об оценке с шагом расчета 0,2 min.
Ts = 0.2; z = iddata(y,u,Ts);
Оцените нелинейную модель ARX.
sys = nlarx(z,[4 4 1]);
Создайте время и массивы данных.
dt = 0.01; t = 0:dt:10; y = 10*sin(2*pi*t)+rand(size(t));
Создайте объект iddata без заданного входного сигнала.
z = iddata(y',[],dt);
Оцените нелинейную модель ARX.
sys = nlarx(z,2);
Загрузите данные об оценке.
load twotankdata;Создайте объект iddata из данных об оценке.
z = iddata(y,u,0.2);
Создайте средство оценки нелинейности сети вейвлета с 5 модулями.
NL = wavenet('NumberOfUnits',5);Оцените нелинейную модель ARX.
sys = nlarx(z,[4 4 1],NL);
Генерация пользовательской сетевой нелинейности требует определения пользовательской модульной функции.
Задайте модуль, функционируют и сохраняют его как gaussunit.m.
% Copyright 2015 The MathWorks, Inc. function [f, g, a] = gaussunit(x) f = exp(-x.*x); if nargout>1 g = -2*x.*f; a = 0.2; end
Создайте пользовательскую сетевую нелинейность с помощью функции gaussunit.
H = @gaussunit; CNet = customnet(H);
Загрузите данные об оценке.
load iddata1;
Оцените нелинейную модель ARX с помощью пользовательской сети.
sys = nlarx(z1,[1 2 1],CNet);
Загрузите данные об оценке.
load motorizedcamera;Создайте объект iddata.
z = iddata(y,u,0.02,'Name','Motorized Camera','TimeUnit','s');
z является объектом iddata с 6 входными параметрами и 2 выходными параметрами.
Задайте порядки модели.
Orders = [ones(2,2),2*ones(2,6),ones(2,6)];
Задайте различные средства оценки нелинейности для каждого выходного канала.
NL = [wavenet('NumberOfUnits',2),linear];Оцените нелинейную модель ARX.
sys = nlarx(z,Orders,NL);
Загрузите данные об оценке и создайте объект iddata.
load motorizedcamera;
z = iddata(y,u,0.02);Задайте порядки модели.
Orders = [ones(2,2),2*ones(2,6),ones(2,6)];
Оцените нелинейную модель ARX с помощью sigmoidnet нелинейности с 4 модулями для всех выходных каналов.
m = nlarx(z,Orders,sigmoidnet('numberOfUnits',4));Загрузите данные об оценке.
load iddata1;Создайте массив ячеек с двумя пользовательскими регрессорами.
C = {'y1(t-1)^2','y1(t-2)*u1(t-3)'};Оцените нелинейную модель ARX с пользовательскими регрессорами и никакими стандартными регрессорами.
sys = nlarx(z1,[0 0 0],'linear','CustomRegressors',C);
Загрузите данные об оценке.
load iddata1;Задайте пользовательский объект регрессора для y1(t-1)^2.
C1 = customreg(@(x)x^2,{'y1'},[1]);Задайте пользовательский объект регрессора для y1(t-2)*u1(t-3).
C2 = customreg(@(x,y)x*y,{'y1','u1'},[2 3]);Создайте пользовательский объектный массив регрессора.
C = [C1,C2];
Оцените нелинейную модель ARX с пользовательскими регрессорами.
sys = nlarx(z1,[0 0 0],'linear','CustomRegressors',C);
Перечислите образцовые регрессоры.
getreg(sys);
Regressors:
y1(t-1)^2
y1(t-2)*u1(t-3)
Загрузите данные об оценке.
load iddata1;Оцените модель Nonlinear ARX с помощью опции 'search'.
sys = nlarx(z1,[4 4 1],'sigmoidnet','NonlinearRegressors','search');
Перечислите образцовые нелинейные индексы регрессора.
sys.NonlinearRegressors
ans = 1×4
3 5 6 7
Перечислите все образцовые регрессоры.
getreg(sys)
Regressors:
y1(t-1)
y1(t-2)
y1(t-3)
y1(t-4)
u1(t-1)
u1(t-2)
u1(t-3)
u1(t-4)
Оптимальный набор нелинейных регрессоров для этой модели включает y1(t-3), u1(t-1), u1(t-2) и u1(t-3).
Загрузите данные об оценке.
load iddata1;Создайте сигмоидальное сетевое средство оценки нелинейности без линейного члена.
SNL = sigmoidnet('LinearTerm','off');
Оцените нелинейную модель ARX.
sys = nlarx(z1,[2 2 1],SNL);
Загрузите данные об оценке.
load throttledata;Детрендируйте данные.
Tr = getTrend(ThrottleData); Tr.OutputOffset = 15; DetrendedData = detrend(ThrottleData,Tr);
Оцените линейную модель ARX.
LinearModel = arx(DetrendedData,[2 1 1]);
Оцените нелинейную модель ARX с помощью линейной модели. Порядки модели, задержки и линейные параметры NonlinearModel выведены от LinearModel.
NonlinearModel = nlarx(ThrottleData,LinearModel);
Загрузите данные об оценке.
load iddata1;Создайте модель idnlarx.
sys = idnlarx([2 2 1]);
Сконфигурируйте модель с помощью записи через точку, чтобы установить следующие параметры:
Используйте сигмоидальную сетевую нелинейность
Ищите оптимальное нелинейное подмножество регрессора
sys.Nonlinearity = 'sigmoidnet'; sys.NonlinearRegressors = 'search';
Оцените нелинейную модель ARX со структурой и свойствами, заданными в объекте idnlarx.
sys = nlarx(z1,sys);
Если оценка останавливается в локальном минимуме, можно встревожить модель с помощью init и повторно оценить модель.
Загрузите данные об оценке.
load iddata1;Оцените первоначальную нелинейную модель с помощью определенных нелинейных регрессоров.
sys1 = nlarx(z1,[4 2 1],'sigmoidnet','NonlinearRegressors',[1:3]);
Случайным образом встревожьте параметры модели, чтобы избежать локальных минимумов.
sys2 = init(sys1);
Оцените новую нелинейную модель со встревоженными значениями.
sys2 = nlarx(z1,sys2);
Загрузите данные об оценке.
load twotankdata;Создайте объект iddata из данных об оценке.
z = iddata(y,u,0.2);
Создайте набор опции nlarxOptions, задающий ошибочную цель минимизации симуляции и максимум 50 итераций оценки.
opt = nlarxOptions;
opt.Focus = 'simulation';
opt.SearchOptions.MaxIterations = 50;Оцените нелинейную модель ARX.
sys = nlarx(z,[4 4 1],'sigmoidnet',opt);Загрузите данные о регуляризации в качестве примера.
load regularizationExampleData.mat nldata;
Создайте нелинейность sigmoidnet с 30 модулями и задайте порядки модели.
NL = sigmoidnet('NumberOfUnits',30);
Orders = [1 2 1];Создайте набор опции оценки и установите метод поиска оценки для lm.
opt = nlarxOptions('SearchMethod','lm');
Оцените неупорядоченную модель.
sys = nlarx(nldata,Orders,NL,opt);
Сконфигурируйте регуляризацию параметр Lambda.
opt.Regularization.Lambda = 1e-8;
Оцените упорядоченную модель.
sysR = nlarx(nldata,Orders,NL,opt);
Сравните эти две модели.
compare(nldata,sys,sysR)

Большой отрицательный результат подгонки для неупорядоченной модели указывает на плохую подгонку к данным. Оценка упорядоченной модели приводит к значительно лучшему результату.
Данные Данные об оценке временного интервалаiddataДанные об оценке временного интервала, заданные как объект iddata. Data может иметь один или несколько выходных каналов и нуля или более входных каналов. Данные должны быть однородно выбраны и не могут содержать недостающий (NaN) выборки.
Orders — Порядки модели и задержкиПорядки модели и задержки определения настройки регрессора, заданной как 1 3 вектор, [na nb nk].
Для модели с ny каналы вывода и каналы входа nu:
na является ny-by-ny матрица, где na(i,j) указывает, что количество регрессоров от j th вывод раньше предсказывало i th вывод.
nb является ny-by-nu матрица, где nb(i,j) указывает, что количество регрессоров от j th вход раньше предсказывало i th вывод.
nk является ny-by-nu матрица, где nk(i,j) указывает, что задержка в j th вход раньше предсказывала i th вывод.
na = [1 2; 2 3] nb = [1 2 3; 2 3 1]; nk = [2 0 3; 1 0 5];
Данные об оценке для этой системы имеют три входных параметров (u1, u2, u3) и два выходных параметров (y1, y2). Полагайте, что регрессоры раньше предсказывали вывод, y2(t):
Поскольку na(2,:) является [2 3], способствующие регрессоры от выходных параметров:
y1(t-1) и y1(t-2)
y2(t-1), y2(t-2) и y2(t-3)
Поскольку nb(2,:) является [2 3 1], и nk(2,:) является [1 0 5], способствующие регрессоры от входных параметров:
u1(t-1) и u1(t-2)
u2(t), u2(t-1) и u2(t-2)
u3(t-5)
Минимальной задержкой для регрессоров на основе выходных переменных является всегда 1, в то время как минимальную задержку для регрессоров на основе входных переменных диктует nk. Используйте getreg, чтобы просмотреть полный набор регрессоров, используемых нелинейной моделью ARX.
Nonlinearity — Средство оценки нелинейности'wavenet' (значение по умолчанию) | 'sigmoidnet' | 'treepartition' | 'linear' | средство оценки нелинейности возражает | массив объектов средства оценки нелинейностиСредство оценки нелинейности, заданное как одно из следующего:
Объект 'wavenet' или wavenet | Сеть Wavelet |
Объект 'sigmoidnet' или sigmoidnet | Сигмоидальная сеть |
Объект 'treepartition' или treepartition | Двоичное дерево |
Объект 'linear' или [] или linear | Линейная функция |
Объект neuralnet | Нейронная сеть — Требует Deep Learning Toolbox™. |
Объект customnet | Пользовательская сеть — Подобно sigmoidnet, но с пользовательской заменой для сигмоидальной функции. |
Для получения дополнительной информации смотрите Доступные Средства оценки Нелинейности для Нелинейных Моделей ARX.
Определение вектора символов, например, 'sigmoidnet', создает объект средства оценки нелинейности с настройками по умолчанию. Также можно задать настройки средства оценки нелинейности двумя способами:
Используйте связанную функцию средства оценки нелинейности с Аргументами пары "имя-значение".
NL = sigmoidnet('NumberOfUnits',10);Создайте и измените объект средства оценки нелинейности по умолчанию.
NL = sigmoidnet; NL.NumberOfUnits = 10;
Для ny каналы вывода можно задать нелинейные средства оценки индивидуально для каждого канала установкой Nonlinearity к ny-by-1 массив объектов средства оценки нелинейности. Чтобы задать ту же нелинейность для всех выходных параметров, задайте Nonlinearity как вектор символов или один объект средства оценки нелинейности.
Пример: 'sigmoidnet' задает сигмоидальную сетевую нелинейность с настройкой по умолчанию.
Пример: treepartition('NumberOfUnits',5) задает нелинейность двоичного дерева с условиями 5 в расширении двоичного дерева.
Пример: [wavenet('NumberOfUnits',10);sigmoidnet] задает различные средства оценки нелинейности для двух выходных каналов.
LinModel — Модель полинома ввода - вывода дискретного времени структуры ARXidpolyМодель полинома ввода - вывода дискретного времени структуры ARX, заданной как модель idpoly. Создайте этот объект с помощью конструктора idpoly или оцените его с помощью команды arx.
sys0 — Nonlinear ARXidnlarxНелинейная модель ARX, заданная как модель idnlarx. sys0 может быть:
Модель ранее оцененное использование nlarx. Алгоритм оценки использует параметры sys0 как исходные предположения. В этом случае используйте init, чтобы немного встревожить образцовые свойства постараться не захватываться в локальных минимумах.
sys = init(sys); sys = nlarx(data,sys);
Модель ранее созданное использование idnlarx и с набором свойств с помощью записи через точку. Используйте этот метод, чтобы избежать сложного синтаксиса Пары "имя-значение" при конфигурировании свойств многоуровневой модели. Например, использовать
sys1 = idnlarx([4 3 1]); sys1.Nonlinearity = 'treepartition'; sys1.CustomRegressors = {'sin(u1(t-1))'}; sys1.NonlinearRegressors = 'search'; sys2 = nlarx(data,sys1);
вместо эквивалента
sys2 = nlarx(data,[4,3,1],'treepartition','CustomRegressors',... {'sin(u1(t-1))'},'NonlinearRegressors','search');
Опции Опции оценкиnlarxOptions установленаУстановлены опции оценки для нелинейной идентификации модели ARX, заданной как опция nlarxOptions.
Укажите необязательные аргументы в виде пар ""имя, значение"", разделенных запятыми. Имя (Name) — это имя аргумента, а значение (Value) — соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
'NonlinearRegressors','output' указывает, что только регрессоры, содержащие выходные переменные, используются в качестве входных параметров к нелинейному блоку модели.'TimeVariable' — Имя независимой переменной't' (значение по умолчанию) | вектор символовИмя независимой переменной, заданное как пара, разделенная запятой, состоящая из 'TimeVariable' и вектора символов. Например, 't'.
'CustomRegressors' — Регрессоры создаются из комбинаций вводов и выводов{} (значение по умолчанию) | массив ячеек из символьных векторов | массив объектов customregРегрессоры, созданные из комбинаций вводов и выводов, заданных как пара, разделенная запятой, состоящая из 'CustomRegressors' и одно из следующего для систем одно вывода:
Массив ячеек из символьных векторов. Например:
{'y1(t-3)^3','y2(t-1)*u1(t-3)','sin(u3(t-2))'}
Каждый вектор символов должен представлять действительную формулу для регрессора, способствующего прогнозу образцового вывода. Формула должна быть записана с помощью имен ввода и вывода и имени переменной времени как переменные.
Массив пользовательских объектов регрессора, созданное использование customreg или polyreg.
Для модели с ny выходные параметры задайте ny-by-1 массив ячеек массивов объектов customreg или символьных массивов.
Эти регрессоры в дополнение к стандартным регрессорам на основе Orders.
Пример: 'CustomRegressors',{'y1(t-3)^3','y2(t-1)*u1(t-3)'}
Пример: 'CustomRegressors',{'sin(u3(t-2))'}
'NonlinearRegressors' — Подмножество регрессоров, которые входят как входные параметры в нелинейный блок модели'all' (значение по умолчанию) | 'output' | 'input' | 'standard' | 'custom' | 'search' | вектор положительных целых чисел | [] | массив ячеекПодмножество регрессоров, которые входят как входные параметры в нелинейный блок модели, заданной как пара, разделенная запятой, состоящая из 'NonlinearRegressors' и одно из следующих значений:
все Все регрессоры
вывод Регрессоры, содержащие выходные переменные
входной параметр Регрессоры, содержащие входные переменные
'standard' — Стандартные регрессоры
'custom' — Пользовательские регрессоры
'search' — Алгоритм оценки выполняет поиск лучшего подмножества регрессора. Это полезно когда это необходимо, чтобы сократить большое количество регрессоров, вводящих нелинейный функциональный блок средства оценки нелинейности. Эта опция должна быть применена ко всем выходным моделям одновременно.
[] — Никакие регрессоры. Это создает линейную в регрессоре модель.
Вектор индексов регрессора. Чтобы определить номер и порядок регрессоров, используйте getreg.
Для модели с несколькими выходными параметрами задайте массив ячеек элементов ny, где ny является количеством выходных каналов. Для каждого вывода задайте одну из предыдущих опций. Также, чтобы применить то же подмножество регрессора ко всем образцовым выходным параметрам, задайте [] или любую из одних только опций вектора символов, например, 'standard'.
Пример: 'NonlinearRegressors','search' выполняет лучший поиск регрессора единственного вывода одной выходной модели или всех выходных параметров кратного выходная модель.
Пример: 'NonlinearReg','input' применяет только входные регрессоры к входным параметрам нелинейной функции.
Пример: 'NonlinearRegressors',{'input','output'} применяет входные регрессоры к первому выводу и выходные регрессоры к второму выводу модели с двумя выходными параметрами.
sys — Nonlinear ARXidnlarxНелинейная модель ARX, которая соответствует данным данным об оценке, возвратилась как объект idnlarx. Эта модель создается с помощью заданных порядков модели, средства оценки нелинейности и опций оценки.
Информация о результатах оценки и используемых опциях хранится в свойстве Report модели. Содержимое Report зависит от выбора нелинейности, и оценка фокусируют вас заданный для nlarx. Report имеет следующие поля:
| Сообщите о поле | Описание | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Status | Сводные данные состояния модели, которое указывает, была ли модель создана конструкцией или получена оценкой. | ||||||||||||||||||
Method | Команда оценки используется. | ||||||||||||||||||
Fit | Количественная оценка оценки, возвращенной как структура. Смотрите Функцию потерь и Образцовые Метрики качества для получения дополнительной информации об этих метриках качества. Структура имеет следующие поля:
| ||||||||||||||||||
Parameters | Ориентировочные стоимости параметров модели. | ||||||||||||||||||
OptionsUsed | Набор опции используется для оценки. Если никакие пользовательские опции не были сконфигурированы, это - набор опций по умолчанию. Смотрите | ||||||||||||||||||
RandState | Состояние потока случайных чисел в начале оценки. Пустой, | ||||||||||||||||||
DataUsed | Атрибуты данных используются для оценки, возвращенной как структура со следующими полями:
| ||||||||||||||||||
Termination | Условия завершения для итеративного поиска используются для ошибочной минимизации прогноза. Структура со следующими полями:
Для методов оценки, которые не требуют числовой оптимизации поиска, не использовано поле |
Для получения дополнительной информации об использовании Report см. Отчет Оценки.
Нелинейная модель ARX состоит из образцовых регрессоров и средства оценки нелинейности. Средство оценки нелинейности включает и линейные и нелинейные функции, которые действуют на образцовые регрессоры, чтобы дать образцовый вывод. Эта блок-схема представляет структуру нелинейной модели ARX в сценарии симуляции.
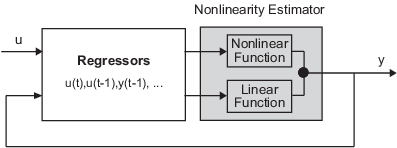
Программное обеспечение вычисляет нелинейную модель ARX вывод y на двух этапах:
Это вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.
В самом простом случае регрессоры являются задержанными вводами и выводами, такими как u (t-1) и y (t-3). Подобные регрессоры называются стандартными регрессорами. Вы задаете стандартные регрессоры с помощью порядков модели и задержки. Для получения дополнительной информации смотрите Нелинейные Порядки Модели ARX и Задержку. Можно также задать пользовательские регрессоры, которые являются нелинейными функциями задержанных вводов и выводов. Например, u (t-1) *y (t-3). Чтобы создать набор полиномиальных регрессоров типа, используйте polyreg.
По умолчанию все регрессоры являются входными параметрами и к линейному и к нелинейным функциональным блокам средства оценки нелинейности. Можно выбрать подмножество регрессоров как входные параметры к нелинейному функциональному блоку.
Это сопоставляет регрессоры с образцовым выводом с помощью блока средства оценки нелинейности. Блок средства оценки нелинейности может включать линейные и нелинейные блоки параллельно. Например:
Здесь, x является вектором регрессоров, и r является средним значением регрессоров x. вывод блока линейной функции и является аффинным когда d ≠ 0. d является скалярным смещением. представляет вывод нелинейного функционального блока. Q является матрицей проекции, которая делает вычисления хорошо подготовленными. Точная форма F (x) зависит от вашего выбора средства оценки нелинейности. Можно выбрать из доступных средств оценки нелинейности, таких как сети древовидного раздела, сети вейвлета и многоуровневые нейронные сети. Можно также исключить или линейное или нелинейный функциональный блок от средства оценки нелинейности.
При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметра модели, такие как L, r, d, Q и другие параметры, задающие g.
Получившиеся нелинейные модели ARX являются объектами idnlarx, которые хранят все данные модели, включая образцовые регрессоры и параметры средства оценки нелинейности. Для получения дополнительной информации об этих объектах, смотрите Нелинейные Образцовые Структуры.
Поддержка параллельных вычислений доступна для оценки с помощью метода поиска lsqnonlin (требует Optimization Toolbox™). Чтобы включить параллельные вычисления, используйте nlarxOptions, установите SearchMethod на 'lsqnonlin' и установите SearchOptions.Advanced.UseParallel на true.
Например:
opt = nlarxOptions;
opt.SearchMethod = 'lsqnonlin';
opt.SearchOptions.Advanced.UseParallel = true;
aic | fpe | goodnessofFit | idnlarx | isnlarx | nlarxOptions
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.