Можно использовать sim, чтобы моделировать систему с обратной связью, состоящую из линейной модели объекта управления и контроллера MPC.
Если ваш объект является нелинейной моделью Simulink®, необходимо линеаризовать объект (см. Linearization Using Linear Analysis Tool в Simulink Control Design), и разработайте контроллер для линейной модели (см. Проект Контроллер MPC в Simulink). Чтобы моделировать систему, задайте контроллер в поле MPC Controller параметров блоков MPC и запустите модель Simulink с обратной связью.
Также ваша нелинейная сила модели быть файлом MEX, или вы можете хотеть включать недоступные функции в блок MPC, такие как пользовательское средство оценки состояния. Функцией mpcmove является Model Predictive Control Toolbox™ вычислительный механизм, и можно использовать его в таких случаях. Недостаток - то, что необходимо копировать инфраструктуру, которую функция sim и блок MPC обеспечивают автоматически.
Модель CSTR, описанная в, Линеаризует Модели Simulink, строго нелинейная система. Как показано в Проекте Контроллер MPC в Simulink, контроллер может отрегулировать этот объект, но ухудшается (и может даже стать нестабильным), если рабочая точка значительно изменяется.
Цель этого примера состоит в том, чтобы переопределить прогнозирующий контроллер в начале каждого интервала управления так, чтобы его прогнозирующая модель, хотя линейный, представляла последние условия объекта максимально точно. Это будет сделано, линеаризуя нелинейную модель неоднократно, позволяя контроллеру адаптироваться, когда условия объекта изменяются. Для получения дополнительной информации на этом подходе, см. [1] и [2].
В следующем коде симуляция начинается в номинальной рабочей точке модели CSTR (концентрация = 8.57) и перемещается в более низкую точку (концентрация = 2), где скорость реакции намного выше. Необходимый код следующие:
[sys, xp] = CSTR_INOUT([],[],[],'sizes'); up = [10 298.15 298.15]; u = up(3); tsave = []; usave = []; ysave = []; rsave = []; Ts = 1; t = 0; while t < 40 yp = xp; % Linearize the plant model at the current conditions [a,b,c,d] = linmod('CSTR_INOUT',xp,up); Plant = ss(a,b,c,d); Plant.InputGroup.ManipulatedVariables = 3; Plant.InputGroup.UnmeasuredDisturbances = [1 2]; Model.Plant = Plant; % Set nominal conditions to the latest values Model.Nominal.U = [0 0 u]; Model.Nominal.X = xp; Model.Nominal.Y = yp; dt = 0.001; simOptions.StartTime = num2str(t); simOptions.StopTime = num2str(t+dt); simOptions.LoadInitialState = 'on'; simOptions.InitialState = 'xp'; simOptions.SaveTime = 'on'; simOptions.SaveState = 'on'; simOptions.LoadExternalInput = 'on'; simOptions.ExternalInput = '[t up; t+dt up]'; simOut = sim('CSTR_INOUT',simOptions); T = simOut.get('tout'); XP = simOut.get('xout'); YP = simOut.get('yout'); Model.Nominal.DX = (1/dt)*(XP(end,:)' - xp(:)); % Define MPC controller for the latest model MPCobj = mpc(Model, Ts); MPCobj.W.Output = [0 1]; % Ramp the setpoint r = max([8.57 - 0.25*t, 2]); % Compute the control action if t <= 0 xd = [0; 0]; x = mpcstate(MPCobj,xp,xd,[],u); end u = mpcmove(MPCobj,x,yp,[0 r],[]); % Simulate the plant for one control interval up(3) = u; simOptions.StartTime = num2str(t); simOptions.StopTime = num2str(t+Ts); simOptions.InitialState = 'xp'; simOptions.ExternalInput = '[t up; t+Ts up]'; simOut = sim('CSTR_INOUT',simOptions); T = simOut.get('tout'); XP = simOut.get('xout'); YP = simOut.get('yout'); % Save results for plotting tsave = [tsave; T]; ysave = [ysave; YP]; usave = [usave; up(ones(length(T),1),:)]; rsave = [rsave; r(ones(length(T),1),:)]; xp = XP(end,:)'; t = t + Ts; end figure(1) plot(tsave,[ysave(:,2) rsave]) title('Residual Concentration') figure(2) plot(tsave,usave(:,3)) title('Coolant Temperature')
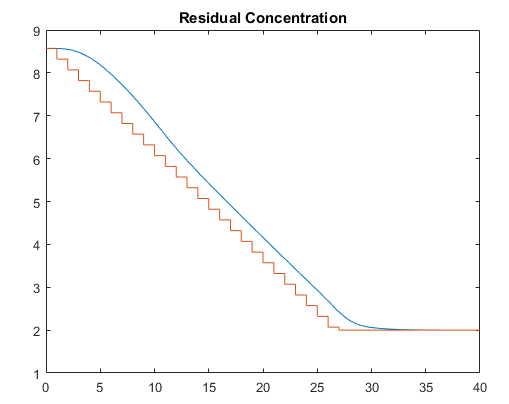
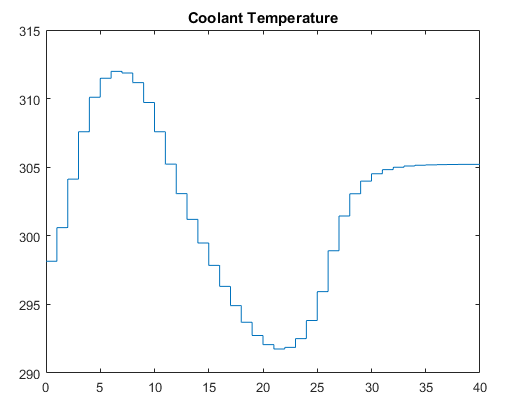
Нанесенные на график результаты появляются ниже. Отметьте следующие моменты:
Заданное значение сползается от начальной концентрации до желаемого окончательного значения (см. пошаговые изменения в реакторном графике концентрации ниже). Реакторная концентрация отслеживает этот пандус гладко с некоторой задержкой (см. плавную кривую), и обосновывается в конечном состоянии с незначительным перерегулированием. Контроллер работает одинаково хорошо (и достигает итоговой концентрации более быстро) для пошагового изменения заданного значения, но она делает нереалистично быстрые изменения в температуре хладагента (не показанными).
Итоговое устойчивое состояние требует температуры хладагента 305.20 K (см. график температуры хладагента ниже). Интересная функция этого нелинейного объекта - то, что, если вы запускаете в начальном устойчивом состоянии (температура хладагента = 298,15 K), продвигаясь, температура хладагента в 305,20 и содержание не достигнет желаемой итоговой концентрации 2. На самом деле в соответствии с этой простой стратегией реакторная концентрация стабилизировалась в окончательном значении 7,88, далекий от требуемого значения. Успешный контроллер должен увеличить реакторную температуру, пока реакция не "взлетает", после которого это должно уменьшить температуру хладагента, чтобы обработать увеличенную загрузку тепла. Подход перелинеаризации предоставляет такому контроллеру (см. следующие графики).
Функциональный linearize повторно линеаризует объект, когда его состояние развивается. Эта функция была обсуждена ранее в Линеаризации Используя код MATLAB.
Код также сбрасывает номинальные условия линейной модели к последним значениям. Обратите внимание, однако, что первые два входных сигнала, которые являются неизмеренными воздействиями в проектировании контроллера, всегда имеют номинальные нулевые значения. Когда они не измерены, диспетчеру нельзя сообщить об истинных значениях. Ненулевое значение вызвало бы ошибку.
Функциональный mpc задает новый контроллер на основе повторно линеаризовавшей модели объекта управления. Выходная настройка веса игнорирует измерение температуры, фокусируясь только на концентрации.
В t = 0, функция mpcstate инициализирует расширенный вектор состояния диспетчера, x, который является объектом mpcstate. После этого функция mpcmove обновляет его автоматически использование средства оценки состояния по умолчанию диспетчера. Также было бы возможно использовать Расширенный фильтр Калмана (EKF), как описано в [1] и [2], в этом случае EKF сбросит входные переменные mpcstate на каждом шаге.
Функция mpcmove использует последнее определение контроллера и состояние, измеренный объект выходные параметры и заданные значения, чтобы вычислить новую температуру хладагента на каждом шаге.
Функция sim Simulink моделирует нелинейный объект с начала в конец интервала управления. Обратите внимание на то, что итоговое условие от предыдущего шага используется в качестве начального состояния объекта, и что входные параметры объекта считаются постоянные во время каждого интервала.
Помните, что обычный контроллер обратной связи или фиксированный контроллер Model Predictive Control Toolbox, настроенный, чтобы действовать при начальном условии, стали бы нестабильными, когда объект перемещается в итоговое условие. Периодическое образцовое обновление преодолевает эту проблему автоматически и обеспечивает превосходное управление при всех условиях.
[1] Ли, J. H. и Н. Л. Рикер, "Расширенный Фильтр Калмана Основанное Нелинейное Образцовое Прогнозирующее Управление", Ind. Инженер Чем. Res., Издание 33, № 6, стр 1530–1541 (1994).
[2] Ricker, N. L. и Дж. Х. Ли "Нелинейное Образцовое Прогнозирующее Управление Процесса проблемы Теннесси Истмэна", Computers & Chemical Engineering, Издание 19, № 9, стр 961–981 (1995).